湖北省武汉市硚口区2021-2021学年九年级上学期10月月考数学试题

试卷更新日期：2022-09-06 类型：月考试卷

进入出卷网下载

一、单选题

1. 将一元二次方程x²＋1＝3x化成一般形式后，二次项系数和一次项系数分别为（）

A、1，－3. B、1，3. C、1，0. D、x² ，－3x.

查看试题解析
2. 方程（x－3）²＝1的解是（）

A、x₁＝1，x₂＝－1 B、x₁＝4，x₂＝2 C、x＝4 D、x＝2

查看试题解析
3. 已知二次函数 $y = (m - 3) x^{m^{2} - 7}$ ，则m的值为（）

A、 $- 3$ B、 $\pm 3$ C、3 D、 $\pm \sqrt{5}$

查看试题解析
4. 将一元二次方程x²＋8x－5＝0化成（x＋a）²＝b（a，b为常数）的形式，则a，b的值分别是（）

A、－4，21 B、－4，11 C、4，21 D、－8，69

查看试题解析
5. 某树主干长出若干数目的支干，每个支干又长出同样数目小分支，主干、支干和小分支总数共91．若设主干长出x个支干，则可列方程正确的是（）

A、（1＋x）²＝91 B、1＋x＋x²＝91 C、1＋x²＝91 D、x＋x²＝91

查看试题解析
6. 杨倩在东京奥运女子10米气步枪决赛中夺得冠军，为中国代表团揽入首枚金牌，随后杨倩同款“小黄鸭”发卡在电商平台上爆单，该款发卡在某电商平台上7月24日的销量为5000个，7月25日和7月26日的总销量是30000个．若7月25日和26日较前一天的增长率均为 $x$ ．则可列方程正确的是（）

A、 $5000 {(1 + x)}^{2} = 30000$ B、 $5000 (1 - x^{2}) = 30000$ C、 $5000 + 5000 (1 + x) + 5000 {(1 + x)}^{2} = 30000$ D、 $5000 (1 + x) + 5000 {(1 + x)}^{2} = 30000$

查看试题解析
7. 抛物线y＝（x―1）²－9经变换后得到抛物线y＝x²＋2x－8，则下列变换正确的是（）

A、向左平移6个单位长度 B、向右平移6个单位长度 C、向左平移2个单位长度 D、向右平移2个单位长度

查看试题解析
8. x₁ ， x₂是一元二次方程x²－ $\sqrt{2}$ x－1＝0的两个实数根﹐则x₁²＋ $\sqrt{2}$ x₂的值是（）

A、1 B、3 C、4 D、 $\sqrt{2}$

查看试题解析
9. 抛物线y＝x²－（4a＋1）x＋3a²＋3a（a为常数）与x轴交于A、B两点，若AB＝2，则a的值是（）

A、 $\frac{3}{2}$ B、－ $\frac{1}{2}$ C、－ $\frac{3}{2}$ 或 $\frac{3}{2}$ D、－ $\frac{1}{2}$ 或 $\frac{3}{2}$

查看试题解析
10. 用总长为a米的材料做成如图1的矩形窗框，设窗框的宽为x米，窗框的面积为y米² ， y关于x的函数图象如图2，则a的值是（）

A、9 B、8 C、6 D、不能确定

查看试题解析

二、填空题

11. 已知x＝1是方程x²＋x＋c＝0的解，则c的值是．

查看试题解析
12. 抛物线y＝－（x－1）²－2的顶点坐标是．

查看试题解析
13. 两个相邻偶数的积是168，设这两个相邻偶数中较大的数是x，可列方程是．

查看试题解析
14. 一名男生推铅球，铅球行进的高度y（单位：米）与水平距离x（单位：米）之间的关系为 $y = - \frac{1}{12} x^{2} + \frac{2}{3} x + \frac{5}{3}$ ，则这名男生这次推铅球的成绩是米．

查看试题解析
15. 如图，抛物线y＝ax²＋bx＋c（a，b，c是常数）经过点(3，0)，对称轴为直线x＝1．下列四个结论：①点P₁(－2020，y₁)，P₂(2023，y₂)在抛物线上，则y₁＞y₂；②2a＋c＜0；③关于x的方程ax²＋bx＋c＝p的两个实数根为m，n（n＜m），若p＞0，则m＜3且n＞－1；④a（1－t²）≥b（t－1）（t为常数）．其中正确的结论是（填写序号）．

查看试题解析
16. 如图，在正方形ABCD 中，AB＝4，点E在BC上，将线段EA绕点E顺时针旋转90°，得到线段EF，连接DE，DF，CF，则 $\frac{C F}{B E}$ 的值是﹔设BE＝x， $△$ DEF面积为S，则S与x之间的关系式是．

查看试题解析

三、解答题

17. 解方程

(1)、4x²＝6x；

(2)、x²＋4x－3＝0．

查看试题解析
18. 关于 $x$ 的一元二次方程 $x^{2} + (2 m - 3) x + m^{2} = 0$ 有两个不相等的实数根．

(1)、求 $m$ 的取值范围；

(2)、若 $x_{1}$ 、 $x_{2}$ 是方程的两根，且 $\frac{1}{x_{1}} + \frac{1}{x_{2}} = 1$ ，求 $m$ 的值．

查看试题解析
19. 如图是一个长18cm，宽15cm 的矩形图案，其中有两条宽度相等，互相垂直的彩条，彩条面积是图案面积的三分之一，求彩条的宽度．

查看试题解析
20. 如图，矩形ABCD的边BC在x轴上，顶点A和D在抛物线y＝－x²＋6x上，设点B的横坐标为t（0＜t＜3），矩形ABCD的周长为l．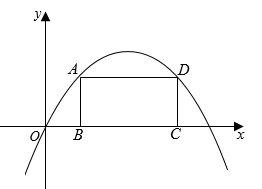

(1)、抛物线的对称轴是；

(2)、若t＝1，直接写出点A的坐标是，点D的坐标是；

(3)、直接写出l与t之间的关系式．

查看试题解析
21. 已知二次函数y＝ax²＋bx＋c中，函数y与自变量x的部分对应值如下表：
x
…
－4
－3
－2
－1
0
1
2
…
y
…
m
0
－3
－4
－3
0
5
…

(1)、观察表格，二次函数图象的对称轴是， m的值是；

(2)、在如图的8×9的正方形网格坐标系中，其图象与x轴交于A，B两点，与y轴交于点C．仅用无刻度的直尺在给定的网格中按要求完成画图并回答问题（用虚线表示画图过程）．
①如图1，点E在射线CO上，点D在直线AC上方的抛物线上，若 $S_{△ A C E} ＝ S_{△ A C D}$ ＝3，直接写出点E的坐标，并画出点D；
②如图2，已知点P(m，n)在第一象限的抛物线上，若点Q的坐标为(－m－2，n)，画出点Q．

查看试题解析
22. 某商品的进价为每件8元，现在的售价为每件10元，每天可卖出200件．市场调查反映：如提高销售价，每涨价0.5元，每天要少卖出10件．

(1)、当涨价2元时，直接写出每天的销售量；

(2)、设该商品的销售价为每件x元（x＞10且是0.5的整数倍），每天的销售利润为w元．
①求w关于x的函数关系式（不需要写出自变量的取值范围）；
②销售价定在多少元时，每天获得的销售利润最大？最大值是多少？

查看试题解析
23. AC，BD是四边形ABCD的对角线，AB＝AC，∠ABC＋∠ADC＝90°．

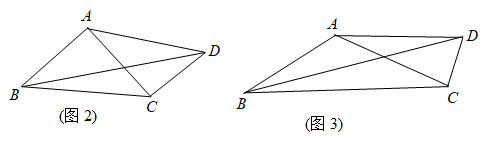(1)、如图1．若∠ABC＝60°，求证：BD²＝AD²＋CD²；请参照大胖同学的思路完成如下证明过程．
证明：以AD为边作等边 $△$ ADE，连接BE，因为∠ABC＝60°，AB＝AC，所以 $△$ ABC是等边三角形，

(2)、如图2，若∠ABC＝45°，写出一个等式，表示BD，AD，CD之间的数量关系，并给出证明；

(3)、如图3，若∠ABC＝30°，AD $/ /$ BC，直接写出 $\frac{A B}{B D}$ 的值．

查看试题解析
24. 抛物线C：y＝ax²＋bx－3与x轴交于A(－1，0)，B(3，0)两点，与y轴交于点C．

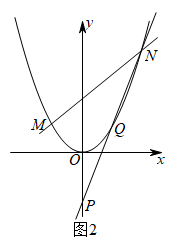(1)、求抛物线的解析式；

(2)、如图1，点D在第四象限的抛物线C上，将绒段DB绕点D逆时针旋转90°，得到线段DE，当点E恰好落在y轴上时，求点D的坐标；

(3)、如图2，已知点P(0，－2)，将抛物线C向左平移1个单位长度﹐向上平移4个单位长度，得到抛物线C₁ ．直线y＝kx＋2（k＞0）交抛物线C₁于M，N两点（M在N的左边），直线NP交抛物线C₁于另－点Q，求证：点M与点Q关于y轴对称．

查看试题解析

x	…	－4	－3	－2	－1	0	1	2	…
y	…	m	0	－3	－4	－3	0	5	…