湖北省武汉市江汉区四校联盟2021~2022学年九年级上学期10月监测数学试题
试卷更新日期:2022-09-06 类型:月考试卷
一、单选题
-
1. 下列图案中不是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 一元二次方程5x2-1-4x=0的二次项系数,一次项系数分别是( )A、5、-1 B、5、-4 C、5、4 D、5、13. 用配方法解方程 ,方程应变形为( ).
2. 一元二次方程5x2-1-4x=0的二次项系数,一次项系数分别是( )A、5、-1 B、5、-4 C、5、4 D、5、13. 用配方法解方程 ,方程应变形为( ).
A、 B、 C、 D、4. 已知方程2x2-x-1=0两根分别是x1和x2 , 则x1+x2的值等于( )A、2 B、 C、 D、-15. 把二次函数y=-x2的图象先向右平移2个单位,再向上平移5个单位后得到一个新图象,则新图象,则新图象所表示的二次函数的解析式是( )A、y=-(x-2)2+5 B、y=-(x+2)2+5 C、y=-(x-2)2-5 D、y=-(x+2)2-56. 对于抛物线 的说法错误的是( )A、抛物线的开口向下 B、抛物线的顶点坐标是(1,-3) C、抛物线的对称轴是直线 D、当 时, 随 的增大而增大7. 为响应全民阅读活动,某校面向社会开放图书馆.自开放以来,进馆人次逐月增加,第一个月进馆200人次,前三个月累计进馆872人次.若进馆人次的月增长率相同,为求进馆人次的月增长率.设进馆人次的月增长率为x,依题意可列方程为( )A、200(1+x)2=872 B、200(1+x)+200(1+x)2=872 C、200(1+x+x2)=872 D、200+200(1+x)+200(1+x)2=8728. 函数y=ax+b和y=ax2+bx+c在同一直角坐标系内的图象大致是( )A、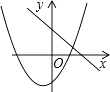 B、
B、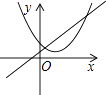 C、
C、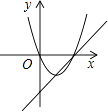 D、
D、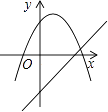 9. 若抛物线y=x2-bx+8的顶点在x轴的负半轴上,则b=( )A、 B、 C、 D、10. 已知:抛物线 经过点 ,且满足 ,以下结论:① ;② ;③ ;④ ,其中正确的个数有( )A、1个 B、2个 C、3个 D、4个
9. 若抛物线y=x2-bx+8的顶点在x轴的负半轴上,则b=( )A、 B、 C、 D、10. 已知:抛物线 经过点 ,且满足 ,以下结论:① ;② ;③ ;④ ,其中正确的个数有( )A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 已知函数 是二次函数,则m=.12. 若关于x的一元二次方程 有两个不相等的实数根,则m的取值范围13. 若抛物线y=-(x-1)2+m的图象上有三点A(-2,y1)、B(1,y2)、C(5,y3),则y1、y2、y3的大小关系为.14. 如图,一副三角板按如图所示叠放在一起,若固定△ABC,将△BDE绕着公共顶点B顺时针旋转α(0°<α<180°).当边DE与△ABC的某一边平行时,相应的旋转角α=
 15. 抛物线 经过点 、 两点,则关于 的一元二次方程 的解是16. 抛物线 上的一个动点P到直线 的最短距离是.
15. 抛物线 经过点 、 两点,则关于 的一元二次方程 的解是16. 抛物线 上的一个动点P到直线 的最短距离是.三、解答题
-
17.(1)、x2-3x+1=0(公式法)(2)、x2+4x-2=018. 已知抛物线 经过点A(-2,-8).
(1)、求a的值,
(2)、若点P(m,-6)在此抛物线上,求点P的坐标.19. 如图,靠着18 m的房屋后墙,围一块150 m2的矩形鸡场.现在童威有篱笆35 m,求矩形鸡场的长与宽. 20. 已知关于x的方程x2﹣2(m+1)x+m2+2=0.(1)、若方程总有两个实数根,求m的取值范围;(2)、若两实数根x1、x2满足(x1+1)(x2+1)=8,求m的值.21. 如图,抛物线y=-x2+(m-1)x+m与y轴交于点(0,3)
20. 已知关于x的方程x2﹣2(m+1)x+m2+2=0.(1)、若方程总有两个实数根,求m的取值范围;(2)、若两实数根x1、x2满足(x1+1)(x2+1)=8,求m的值.21. 如图,抛物线y=-x2+(m-1)x+m与y轴交于点(0,3) (1)、当x满足时,y的值随x值的增大而减小;(2)、当x满足0≤x≤4时,y的取值范围是;(3)、点P为抛物线上一点,且S△APC= ,求点P的坐标.22. 九(4)班数学兴趣小组经过市场调查,整理出童威的某种高端商品在第x(1≤x≤90)天的售价与销量的相关信息如下表:
(1)、当x满足时,y的值随x值的增大而减小;(2)、当x满足0≤x≤4时,y的取值范围是;(3)、点P为抛物线上一点,且S△APC= ,求点P的坐标.22. 九(4)班数学兴趣小组经过市场调查,整理出童威的某种高端商品在第x(1≤x≤90)天的售价与销量的相关信息如下表:时间x(天)
1≤x<50
50≤x≤90
售价(元/件)
x+40
90
每天销售(件)
200-2x
已知该商品的进价为每件30元,设销售该商品的每天利润为y元.
(1)、求出y与x的函数关系式;(2)、问销售该商品第几天时,当天销售利润最大,最大利润是多少?(3)、该商品在前49天销售中,每销售一件商品就捐赠m元(0<m<10)给希望工程.若前49天销售获得的最大日利润为5408元,则m=.23. 已知正方形ABCD与正方形CEFG,M是AF的中点,连接DM、EM. (1)、如图1,点E在CD上,点G在BC的延长线上,请判断DM、EM的数量关系与位置关系,并证明;(2)、如图2,点E在DC的延长线上,点G在BC上,(1)中结论是否仍然成立?请证明你的结论;(3)、如图3,连接BG,N为BG中点.若AB=13,CE=5,则MN的最大值为.24. 如图,已知点P在抛物线 上,点F(0,2)在y轴上,直线l:y=-2与y轴交于点H,PM⊥l于M.
(1)、如图1,点E在CD上,点G在BC的延长线上,请判断DM、EM的数量关系与位置关系,并证明;(2)、如图2,点E在DC的延长线上,点G在BC上,(1)中结论是否仍然成立?请证明你的结论;(3)、如图3,连接BG,N为BG中点.若AB=13,CE=5,则MN的最大值为.24. 如图,已知点P在抛物线 上,点F(0,2)在y轴上,直线l:y=-2与y轴交于点H,PM⊥l于M. (1)、如图1,若点P的横坐标为6,则PF= , PM=;(2)、当∠FPM=60°时,求P点的坐标;(3)、如图2,点P关于y轴对称点Q,点A为抛物线上另一动点,PA交y轴于点M,AQ交y轴于点N,求证:OM=ON.
(1)、如图1,若点P的横坐标为6,则PF= , PM=;(2)、当∠FPM=60°时,求P点的坐标;(3)、如图2,点P关于y轴对称点Q,点A为抛物线上另一动点,PA交y轴于点M,AQ交y轴于点N,求证:OM=ON.