湖北省咸宁市通城县2021-2022学年九年级上学期10月月考数学试题

试卷更新日期：2022-09-06 类型：月考试卷

进入出卷网下载

一、单选题

1. 下列函数中，是二次函数的是（　　　）

A、 $y = x^{2} + \frac{1}{x}$ B、 $y = 3 x - \frac{1}{2} x^{2}$ C、 $y = x (x^{2} + 1)$ D、 $y = - 2 x + 1$

查看试题解析
2. 抛物线 $y = - {(x - 1)}^{2} + 2$ 的顶点坐标是（）

A、 $(1, 2)$ B、 $(- 1, 2)$ C、 $(1, - 2)$ D、 $(- 1, - 2)$

查看试题解析
3. 若二次函数 $y = x^{2} + 3 x + a - 1$ 的图象经过原点，则a的值为（）

A、 $0$ B、 $1$ C、 $- 1$ D、 $1$ 或 $- 1$

查看试题解析
4. 若方程x²＋4x＋a＝0无实根，化简 $\sqrt{16 - 8 a + a^{2}}$ 等于（）

A、4﹣a B、a﹣4 C、﹣（a＋4） D、无法确定

查看试题解析
5. 方程 $(m^{2} - 1) x^{2} + m x - 5 = 0$ 是关于x的一元二次方程，则m满足的条件是（）．

A、 $m \neq 1$ B、 $m \neq 0$ C、 $m \neq - 1$ D、 $m \neq \pm 1$

查看试题解析
6. 已知关于x的方程 $x^{2} - 7 x + 6 a = 0$ 的一个解是 $x_{1} = 2 a$ ，则原方程的另一个解是（）

A、 $x_{2} = 0$ 或7 B、 $x_{2} = 3$ 或4 C、 $x_{2} = 3$ 或7 D、 $x_{2} = 4$ 或7

查看试题解析
7. 抛物线 $y = m x^{2} + 3 m x + 2 (m < 0)$ 经过点 $A (a ， y_{1})$ 、 $B (1 ， y_{2})$ 两点，若 $y_{1} > y_{2}$ ，则实数a满足（）

A、 $- 4 < a < 1$ B、 $a < - 4$ 或 $a > 1$ C、 $- 4 < a \leq - \frac{3}{2}$ D、 $- \frac{3}{2} \leq a < 1$

查看试题解析
8. 关于m的一元二次方程 $\sqrt{7} n m^{2} - n^{2} m - 2 = 0$ 的一个根为2，则 $n^{2} + n^{- 2}$ 的值是（）

A、25 B、26 C、27 D、1

查看试题解析

二、填空题

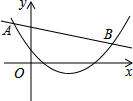
9. 如果抛物线经过点 A(2，5) 和点 B (-4，5) ，那么这条抛物线的对称轴是直线．

查看试题解析
10. 若y=（a+3）x^|a|^﹣1﹣3x+2是二次函数，则a的值为.

查看试题解析
11. 把方程 $(2 x + 1) \cdot (x - 3) = x^{2} + 1$ 化成一般式后，二次项系数、一次项系数、常数项的和为．

查看试题解析
12. 关于x的一元二次方程（a﹣5）x²﹣4x﹣1＝0有实数根，则a的范围是．

查看试题解析
13. 已知一个直角三角形的两条直角边的长恰好是方程 $x^{2} - 17 x + 50 = 0$ 的两个根，则这个直角三角形的斜边长为．

查看试题解析
14. 已知如图二次函数y₁=ax²+bx+c（a≠0）与一次函数y₂=kx+m（k≠0）的图象相交于点A（-2，4），B（8，2）（如图所示）则能使y₁＜y₂成立的x的取值范围是．

查看试题解析
15. 已知二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的对称轴为直线 $x = - 1$ ，与 $x$ 轴的一个交点 $B$ 的坐标为 $(1 ， 0)$ 其图象如图所示，下列结论：① $a b c < 0$ ；② $2 a - b = 0$ ；③当 $y > 0$ 时， $x > 1$ ；④ $3 b + 2 c > 0$ ；⑤当 $x < 0$ 时，y随x的增大而减小；其中正确的有．（只填序号）

查看试题解析
16. 已知关于 $x$ 的方程 $x^{2} - (a^{2} - 2 a - 15) x + a - 1 = 0$ 两个根是互为相反数，则 $a$ 的值为.

查看试题解析

三、解答题

17. 如图，抛物线 $y = - x^{2} + 4 x + n$ 经过点 $A (1 ， 0)$ ，与y轴交于点B.过点B且平行于x轴的直线交抛物线于点C．

(1)、求抛物线的解析式；

(2)、求 $△ A B C$ 的面积；

(3)、在该抛物线的对称轴上是否存在点P，使得 $△ A B P$ 的周长最小？若存在，求出P点的坐标；若不存在，请说明理由．

查看试题解析
18. 已知二次函数 $y = - x^{2} + b x + c$ 的图象与x轴的一个交点坐标为 $(- 1 ， 0)$ ，与y轴的交点坐标为 $(0 ， 3)$ ．

(1)、求此二次函数的解析式；

(2)、用配方法求此抛物线的顶点坐标．

查看试题解析
19. 解方程：

(1)、x²﹣2x﹣99＝0．

(2)、（2x+3）²＝4（2x+3）．

查看试题解析
20. 已知：关于x的方程x²﹣（k+2）x+2k=0

(1)、求证：无论k取任何实数值，方程总有实数根；

(2)、若等腰三角形ABC的一边长a=1，另两边长b，c恰好是这个方程的两个根，求△ABC的周长．

查看试题解析
21. 阅读：我们约定，在平面直角坐标系中，经过某点且平行于坐标轴或平行于两坐标轴夹角角平分线的直线，叫该点的“特征线” $.$ 例如，点 $M (1 ， 3)$ 的特征线有： $x = 1$ ， $y = 3$ ， $y = x + 2$ ， $y = - x + 4 .$ 如图所示．在平面直角坐标系中有正方形 $O A B C$ ，点B在第一象限，A、C分别在x轴和y轴上，抛物线： $y = \frac{1}{4} (x - a)^{2} + b$ 经过B、C两点，顶点D在正方形内部．

(1)、写出点 $M (2 ， 3)$ 任意两条特征线；

(2)、若点D有一条特征线是 $y = x + 1$ ，则求此抛物线的解析式．

查看试题解析
22. 某商场销售一批名牌衬衫：平均每天可售出20件，每件盈利40元，为了扩大销售量，增加盈利，尽快减少库存，商场决定采取适当的降价措施，经市场调查发现：如果每件衬衫降价1元，那么平均每天就可多售出2件.若商场想平均每天盈利达1200元，那么每件衬衫应降价多少元？你若是商场经理，为获得最大利润，每件衬衫应降价多少元，此时最大利润是多少？

查看试题解析
23. 如图，在 $△ A B C$ 中， $∠ B = 9 0^{∘}$ ， $A B = 12 c m$ ， $B C = 24 c m$ ，动点P从点A开始沿着边 $A B$ 向点B以 $2 c m / s$ 的速度移动（不与点B重合），动点Q从点B开始沿着边 $B C$ 向点C以 $4 c m / s$ 的速度移动（不与点C重合）．若P、Q两点同时移动 $t (s)$ ；

(1)、当移动几秒时， $△ B P Q$ 的面积为 $32 c m^{2}$ ．

(2)、设四边形 $A P Q C$ 的面积为 $S (c m^{2})$ ，当移动几秒时，四边形 $A P Q C$ 的面积为 $108 c m^{2}$ ？

查看试题解析
24. 阅读材料：如果 $x_{1}$ ， $x_{2}$ 是一元二次方程 $a x^{2} + b x + c = 0$ 的两根，那么有 $x_{1} + x_{2} = - \frac{b}{a}$ ， $x_{1} x_{2} = \frac{c}{a}$ ．这是一元二次方程根与系数的关系，我们利用它可以用来解题，例 $x_{1}$ ， $x_{2}$ 是方程 $x^{2} + 6 x - 3 = 0$ 的两根，求 $x_{1}^{2} + x_{2}^{2}$ 的值．解法可以这样：
∵ $x_{1} + x_{2} = - 6$ ， $x_{1} x_{2} = - 3$ ，则 $x_{1}^{2} + x_{2}^{2} = (x_{1} + x_{2})^{2} - 2 x_{1} x_{2} = (- 6)^{2} - 2 \times (- 3) = 42$ ．
请你根据以上解法解答下题：
已知 $x_{1}$ ， $x_{2}$ 是方程 $x^{2} + x - 1 = 0$ 的两根，求：

(1)、 $\frac{1}{x_{1}} + \frac{1}{x_{2}}$ 的值；

(2)、 $(x_{1} - x_{2})^{2}$ 的值．

(3)、试求 $x_{2}^{2} - x_{1}^{2}$ 的值．

查看试题解析