四川省资阳市2022年中考数学试卷
试卷更新日期:2022-09-06 类型:中考真卷
一、单选题
-
1. ﹣3的绝对值是( )A、﹣3 B、3 C、- D、2. 如图是正方体的表面展开图,每个面内都分别写有一个字,则与“创”字相对面上的字是( )
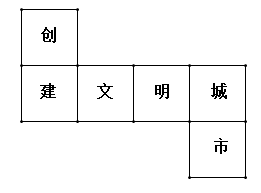 A、文 B、明 C、城 D、市3. 下列计算正确的是( )A、 B、 C、 D、4. 按疫情防控要求,学校严格执行“一日三检”.小明记录某周周一至周五的展检体温(单位:)结果分别为:36.2,36.0,35.8,36.2,36.3.则这组数据的中位数和众数分别是( )A、36.0、36.2 B、36.2、36.2 C、35.8、36.2 D、35.8、36.15. 将直尺和三角板按如图所示的位置放置.若 , 则度数是( )
A、文 B、明 C、城 D、市3. 下列计算正确的是( )A、 B、 C、 D、4. 按疫情防控要求,学校严格执行“一日三检”.小明记录某周周一至周五的展检体温(单位:)结果分别为:36.2,36.0,35.8,36.2,36.3.则这组数据的中位数和众数分别是( )A、36.0、36.2 B、36.2、36.2 C、35.8、36.2 D、35.8、36.15. 将直尺和三角板按如图所示的位置放置.若 , 则度数是( ) A、 B、 C、 D、6. 如图,M、N、P、Q是数轴上的点,那么在数轴上对应的点可能是( )
A、 B、 C、 D、6. 如图,M、N、P、Q是数轴上的点,那么在数轴上对应的点可能是( )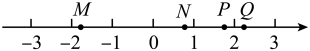 A、点A B、点N C、点P D、点Q7. 如图所示,在中,按下列步骤作图:
A、点A B、点N C、点P D、点Q7. 如图所示,在中,按下列步骤作图:第一步:在上分别截取 , 使;
第二步:分别以点D和点E为圆心、适当长(大于的一半)为半径作圆弧,两弧交于点F;
第三步:作射线交于点M;
第四步:过点M作于点N.
下列结论一定成立的是( )
 A、 B、 C、 D、8. 如图,正方形的对角线交于点O,点E是直线上一动点.若 , 则的最小值是( )
A、 B、 C、 D、8. 如图,正方形的对角线交于点O,点E是直线上一动点.若 , 则的最小值是( ) A、 B、 C、 D、9. 如图.将扇形翻折,使点A与圆心O重合,展开后折痕所在直线l与交于点C,连接 . 若 , 则图中阴影部分的面积是( )
A、 B、 C、 D、9. 如图.将扇形翻折,使点A与圆心O重合,展开后折痕所在直线l与交于点C,连接 . 若 , 则图中阴影部分的面积是( )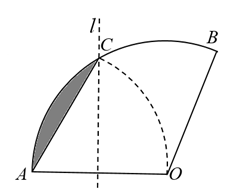 A、 B、 C、 D、10. 如图是二次函数的图象,其对称轴为直线 , 且过点 . 有以下四个结论:① , ② , ③ , ④若顶点坐标为 , 当时,y有最大值为2、最小值为 , 此时m的取值范围是 . 其中正确结论的个数是( )
A、 B、 C、 D、10. 如图是二次函数的图象,其对称轴为直线 , 且过点 . 有以下四个结论:① , ② , ③ , ④若顶点坐标为 , 当时,y有最大值为2、最小值为 , 此时m的取值范围是 . 其中正确结论的个数是( )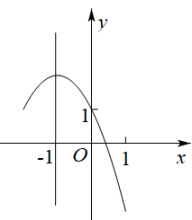 A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题
-
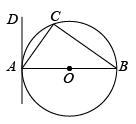
11. 根据国家统计局开展的“带动三亿人参与冰雪运动”调查报告数据显示,全国冰雪运动参与人数达到3.46亿人,成功实现了“三亿人参与冰雪运动”的宏伟目标.数3.46亿用科学记数法表示为 .12. 小张同学家要装修,准备购买两种边长相同的正多边形瓷砖用于铺满地面.现已选定正三角形瓷砖,则选的另一种正多边形瓷砖的边数可以是 . (填一种即可)13. 投掷一枚六个面分别标有1、2、3、4、5、6的质地均匀的正方体骰子,则偶数朝上的概率是 .14. 若a是一元二次方程的一个根,则的值是 .15. 如图,内接于是直径,过点A作的切线 . 若 , 则的度数是度.
 16. 女子10千米越野滑雪比赛中,甲、乙两位选手同时出发后离起点的距离x(千米)与时间(分钟)之间的函数关系如图所示,则甲比乙提前分钟到达终点.
16. 女子10千米越野滑雪比赛中,甲、乙两位选手同时出发后离起点的距离x(千米)与时间(分钟)之间的函数关系如图所示,则甲比乙提前分钟到达终点.
三、解答题
-
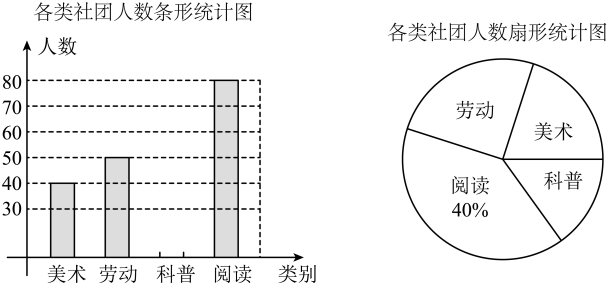
17. 先化简,再求值. , 其中 .18. 某学校为满足学生多样化学习需求,准备组建美术、劳动、科普、阅读四类社团.学校为了解学生的参与度,随机抽取了部分学生进行调查,将调查结果绘制成如图所示的不完整的统计图.请根据图中的信息,解答下列问题:
 (1)、求本次调查的学生人数,并补全条形统计图;(2)、若全校共有学生3600人,求愿意参加劳动类社团的学生人数;(3)、甲、乙两名同学决定在阅读、美术、劳动社团中选择参加一种社团,请用树状图或列表法表示出所有等可能结果,并求出恰好选中同一社团的概率.19. 北京冬奥会吉祥物“冰墩墩”深受大家的喜爱,人们争相购买.现有甲、乙两种型号的“冰墩墩”,已知一个甲种型号比一个乙种型号多20元,购买甲、乙两种型号各10个共需1760元.(1)、求甲、乙两种型号的“冰墩墩”单价各是多少元?(2)、某团队计划用不超过4500元购买甲、乙两种型号的“冰墩墩”共50个,求最多可购买多少个甲种型号的“冰墩墩”?20. 如图,在中 , 过点C作 , 在上截取 , 上截取 , 连接 .
(1)、求本次调查的学生人数,并补全条形统计图;(2)、若全校共有学生3600人,求愿意参加劳动类社团的学生人数;(3)、甲、乙两名同学决定在阅读、美术、劳动社团中选择参加一种社团,请用树状图或列表法表示出所有等可能结果,并求出恰好选中同一社团的概率.19. 北京冬奥会吉祥物“冰墩墩”深受大家的喜爱,人们争相购买.现有甲、乙两种型号的“冰墩墩”,已知一个甲种型号比一个乙种型号多20元,购买甲、乙两种型号各10个共需1760元.(1)、求甲、乙两种型号的“冰墩墩”单价各是多少元?(2)、某团队计划用不超过4500元购买甲、乙两种型号的“冰墩墩”共50个,求最多可购买多少个甲种型号的“冰墩墩”?20. 如图,在中 , 过点C作 , 在上截取 , 上截取 , 连接 .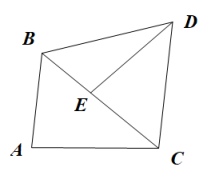 (1)、求证:;(2)、若 , 求的面积.21. 如图,一次函数的图象与反比例函数的图象交于点和点 .
(1)、求证:;(2)、若 , 求的面积.21. 如图,一次函数的图象与反比例函数的图象交于点和点 .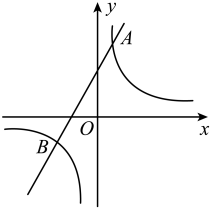 (1)、求一次函数的表达式;(2)、结合图象,写出当时,满足的x的取值范围;(3)、将一次函数的图象平移,使其经过坐标原点.直接写出一个反比例函数表达式,使它的图像与平移后的一次函数图象无交点.22. 小明学了《解直角三角形》内容后,对一条东西走向的隧道进行实地测量.如图所示,他在地面上点C处测得隧道一端点A在他的北偏东方向上,他沿西北方向前进米后到达点D,此时测得点A在他的东北方向上,端点B在他的北偏西方向上,(点A、B、C、D在同一平面内)
(1)、求一次函数的表达式;(2)、结合图象,写出当时,满足的x的取值范围;(3)、将一次函数的图象平移,使其经过坐标原点.直接写出一个反比例函数表达式,使它的图像与平移后的一次函数图象无交点.22. 小明学了《解直角三角形》内容后,对一条东西走向的隧道进行实地测量.如图所示,他在地面上点C处测得隧道一端点A在他的北偏东方向上,他沿西北方向前进米后到达点D,此时测得点A在他的东北方向上,端点B在他的北偏西方向上,(点A、B、C、D在同一平面内) (1)、求点D与点A的距离;(2)、求隧道的长度.(结果保留根号)23. 如图,平行四边形中,边上的高 , 点E为边上的动点(不与B、C重合,过点E作直线的垂线,垂足为F,连接 .
(1)、求点D与点A的距离;(2)、求隧道的长度.(结果保留根号)23. 如图,平行四边形中,边上的高 , 点E为边上的动点(不与B、C重合,过点E作直线的垂线,垂足为F,连接 . (1)、求证:;(2)、当点E为的中点时,求的长;(3)、设的面积为y,求y与x之间的函数关系式,并求当x为何值时,y有最大值,最大值是多少?24. 已知二次函数图象的顶点坐标为 , 且与x轴交于点 .
(1)、求证:;(2)、当点E为的中点时,求的长;(3)、设的面积为y,求y与x之间的函数关系式,并求当x为何值时,y有最大值,最大值是多少?24. 已知二次函数图象的顶点坐标为 , 且与x轴交于点 . (1)、求二次函数的表达式;(2)、如图,将二次函数图象绕x轴的正半轴上一点旋转 , 此时点A、B的对应点分别为点C、D.
(1)、求二次函数的表达式;(2)、如图,将二次函数图象绕x轴的正半轴上一点旋转 , 此时点A、B的对应点分别为点C、D.①连结 , 当四边形为矩形时,求m的值;
②在①的条件下,若点M是直线上一点,原二次函数图象上是否存在一点Q,使得以点B、C、M、Q为顶点的四边形为平行四边形,若存在,求出点Q的坐标;若不存在,请说明理由.