湖北省孝感市云梦县2021-2022学年八年级上学期10月月考数学试题

试卷更新日期：2022-09-06 类型：月考试卷

进入出卷网下载

一、单选题

1. 已知△ABC 有一个内角为 100°，则△ABC 一定是（）

A、锐角三角形 B、钝角三角形 C、直角三角形 D、锐角三角形或钝角三角形

查看试题解析
2. 下列生活中的一些事实运用了“三角形稳定性”的是（）

A、 B、 C、 D、

查看试题解析
3. 在Rt△ABC中，若一个锐角等于40°，则另一个锐角的度数为（　　）

A、40° B、45° C、50° D、60°

查看试题解析
4. 已知三角形的两边长分别是4和6，则此三角形的第三边长可能是（）

A、1 B、2 C、6 D、10

查看试题解析
5. 下列说法正确的是（）

A、两个面积相等的三角形是全等图形 B、两个长方形是全等图形 C、两个周长相等的圆是全等图形 D、两个正方形是全等图形

查看试题解析
6. 如图所示， $∠ 1 = ∠ 2 = 145 °$ ，则 $∠ 3 =$ （）

A、 $80 °$ B、 $70 °$ C、 $60 °$ D、 $50 °$

查看试题解析
7. 如图，在四边形ABCD中，∠ACB＝∠DAC ，添加一个条件后不能保证△BAC≌△DCA是（　　）

A、AB∥CD B、∠B＝∠D C、AB＝CD D、AD＝BC

查看试题解析
8. 如图，在△ABC中， $∠ B A C$ 和 $∠ A B C$ 的平分线 $A E$ 、 $B F$ 相交于点 $O$ ， $A E$ 交 $B C$ 于 $E$ ， $B F$ 交 $A C$ 于 $F$ ，过点 $O$ 作OD $⊥$ BC于 $D$ ，下列四个结论：① $∠ A O B = 90 ° + ∠ C$ ；②当 $∠ C = 60 °$ 时， $A F + B E = A B$ ；③若 $O D = a$ ， $A B + B C + C A = 2 b$ ，则 $S_{△ A B C} = a b$ ．其中正确的是（）

A、①② B、②③ C、①②③ D、①③

查看试题解析

二、填空题

9. 五边形的外角和等于．

查看试题解析
10. 如图，已知点D是△ABC的边BC的中点，点E是边AC的中点，且△ABC的面积为20 $c m^{2}$ ，则△DEC的面积是 $c m^{2}$ .

查看试题解析
11. 若从一个多边形一个顶点出发，最多可以引12条对角线，则它的边数为．

查看试题解析
12. 如图所示， $△ A B C ≌ △ E C D$ ， $∠ A = 48 °$ ， $∠ D = 62 °$ ，则图中 $∠ B$ 的度数是度．

查看试题解析
13. 如图， $A D / / B C$ ， $A D = B C = 4$ ，且三角形 $A B C$ 的面积为 $6$ ，则点 $C$ 到 $A D$ 的距离是．

查看试题解析
14. 如图，一块余料 $A B C D$ ， $A D / / B C$ ，现进行如下操作：以点 $B$ 为圆心，适当长为半径作圆弧，分别交 $B A$ ， $B C$ 于点 $G$ ， $H$ ；再分别以点 $G$ ， $H$ 为圆心，大于 $\frac{1}{2} G H$ 的长为半径作圆弧，两弧在 $∠ A B C$ 内部相交于点 $O$ ，画射线 $B O$ ，交 $A D$ 于点 $E$ ．连结 $O G$ 、 $O H$ ．若 $∠ A = 124 °$ ，则 $∠ A E B$ 的度数为度．

查看试题解析
15. 已知△ABC的高为AD，BE相交于O点，∠C =70°，则∠BOA的度数为

查看试题解析
16. 如图，已知五边形ABCDE中，∠ABC=∠AED=90°，AB=CD=AE=BC+DE=2，则五边形ABCDE的面积为.

查看试题解析

三、解答题

17. 画出图中多边形的所有对角线．

查看试题解析
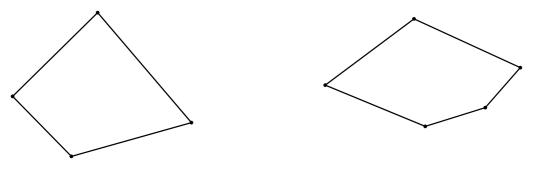18. 如图，在 $△$ ABC中，过AB上任意一点D作 $D E / / A C$ 交BC于点E，以E为顶点，ED为一边，作∠DEF＝∠A，另一边EF交AC于F．

(1)、EF与AB平行吗？说明理由；

(2)、若∠ABC＝30°，∠ACB＝40°，则∠EFC的度数为．

查看试题解析
19. 如图，在 $△ A B C$ 中， $A C = B C$ ， $C D ⊥ A B$ ，求证： $C D$ 平分 $∠ A C B$ ．

查看试题解析
20. 如图，BM，CN分别是△ABC的高，点P在高BM上，点Q在高CN所在的直线上，且BP＝AC，CQ＝AB，请问AP与AQ有什么样的关系？说明理由．

查看试题解析
21. 如图，在平面直角坐标系中，△ABC的顶点均在网格的格点处．

(1)、请写出A，B，C的坐标；

(2)、请求出△ABC的面积；

(3)、若点P在x轴上，且△PAB的面积与△ABC的面积相等，请直接写出点P的坐标．

查看试题解析
22. 如图，在△ABC中，AB＝AC，E在线段AC上，D在线段AB的延长线上，连DE交BC于F，过点E作EG⊥BC于G，若BD＝CE，求证：FG＝BF＋CG．

查看试题解析
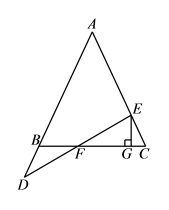23. 在△ABC中，∠ABC与∠ACB的平分线相交于点P．

(1)、如图①，若∠BPC＝α，则∠A＝；（用α的代数式表示，请直接写出结论）

(2)、如图②，作△ABC外角∠MBC、∠NCB的角平分线交于点Q，试探究∠Q与∠BPC之间的数量关系，并说明理由；

(3)、如图③，延长线段CP、QB交于点E，△CQE中，存在一个内角等于另一个内角的2倍，求∠A的度数．

查看试题解析
24. 如图1，在Rt△ABC中，∠C=90°，AD平分∠BAC，BE平分∠ABC，AD、BE相交于点F．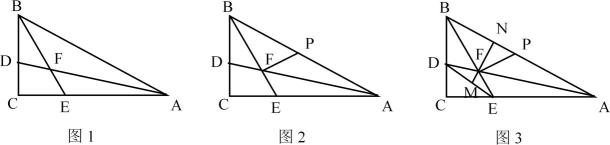

(1)、求∠AFE的度数；

(2)、如图2，过点F作FP⊥BE交AB于点P，求证：EF＝FP；

(3)、如图3，在（2）的条件下，连接DE，过点F作FN⊥AB于点N，并延长NF交DE于点M，试判断DM与EM的数量关系，并说明理由．

查看试题解析