湖北省十堰市郧西县2021-2022学年八年级上学期10月月考数学试题
试卷更新日期：2022-09-06 类型：月考试卷
一、单选题
-
1. 在下列长度的三条线段中，不能组成三角形的是（ ）A、2 cm， 3 cm. 4cm B、3 cm， 6 cm. 6cm C、2 cm， 2 cm， 6cm D、5 cm， 6 cm. 7 cm2. 下面四个图形中，线段BE能表示三角形ABC的高的是（ ）A、
B、
C、
D、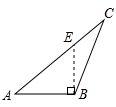
3. 如图，把长短确定的两根木棍AB、AC的一端固定在A处，和第三根木棍BM摆出△ABC，木棍AB固定，木棍AC绕A转动，得到△ABD，这个实验说明（ ）
A、△ABC与△ABD不全等 B、有两边分别相等的两个三角形不一定全等 C、两边和它们的夹角分别相等的两个三角形全等 D、有两边和其中一边的对角分别相等的两个三角形不一定全等4. 如图，AB=DB，BC=BE，欲证△ABE≌△DBC，则可增加的条件是（ ）
A、∠ABE=∠DBE B、∠A=∠D C、∠E=∠C D、∠1=∠25. 如如图， Rt△ABC中，∠C=90°，AD是∠BAC的平分线，DE⊥AB，垂足为E，若AB=10cm，AC=6cm，则BE的长度是（ ）
A、 B、 C、 D、6. 过多边形的一个顶点可以引出6条对角线，则多边形的边数是（ ）A、7 B、8 C、9 D、107. 如图，四边形ABCD中，若去掉一个60°的角后得到一个五边形，则∠1+∠2等于（ ）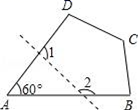
A、120° B、180° C、240° D、300°8. 如图，△ABC的三边AB、BC、AC的长分别12，18，24，O是△ABC三条角平分线的交点，则S△OAB：S△OBC：S△OAC=（ ）
A、1：1：1 B、1：2：3 C、2：3：4 D、3：4：59. 如图，点D是的边上任意一点，点E、F分别是线段的中点，若的面积为S，则的面积等于（ ）
A、 B、 C、 D、10. 如图，已知线段AB＝20米，MA⊥AB于点A，MA＝6米，射线BD⊥AB于B，P点从B点向A运动，每秒走1米，Q点从B点向D运动，每秒走3米，P、Q同时从B出发，则出发x秒后，在线段MA上有一点C，使△CAP与△PBQ全等，则x的值为（ ）
A、5 B、5或10 C、10 D、6或10二、填空题
-
11. 已知三角形的两边长分别为2和4，那么第三边c的取值范围是 ．12. 若n边形的每个内角都等于150°，则n= ．13. 如图， ， ， 则 ．
14. 如图，点B的坐标为（4，4），作BA⊥x轴，BC⊥y轴，垂足分别为A，C，点D为线段OA的中点，点P从点A出发，在线段AB、BC上沿A→B→C运动，当OP=CD时，点P的坐标为 ．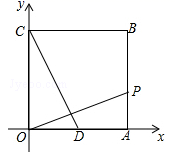
15. 如图，点O在△ABC内，且到三边的距离相等，若∠A=60°，则∠BOC= ．
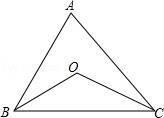16. 如图，在△ABC中，∠C＝40°，将△ABC沿着直线l折叠，点C落在点D的位置，则∠1﹣∠2的度数是 ．
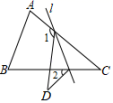17. 如图，BD平分∠ABC，DE⊥AB于E，DF⊥BC于F，AB=6，BC=8．若S△ABC=28，则DE= ．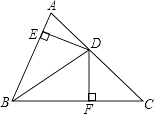
三、解答题
-
18. △ABC中，∠B＝∠C+10°，∠A＝∠B+10°，求△ABC的各内角的度数.19. 已知一个多边形的内角和比它的外角和的3倍少180°，求这个多边形的边数和对角线的条数．20. 如图，点B、E、C、F在同一条直线上，AB＝DE，AC＝DF，BE＝CF，求证：AB∥DE．
21. 如图所示，点A、E、F、C在同一直线上，AE=CF，过E、F分别作DE⊥AC，BF⊥AC，且AB=CD，
(1)、AB与CD平行吗？若平行请说明理由；(2)、证明BD平分EF.22. 如图，△ABC中，D是BC延长线上一点，满足CD＝AB，过点C作CE∥AB且CE＝BC，连接DE并延长，分别交AC、AB于点F、G.
(1)、求证：△ABC≌△DCE；(2)、若∠B＝50°，∠D＝22°，求∠AFG的度数.23. 在ΔABC中，∠ABC的平分线与∠ACB的外角∠ACE的平分线相交于点D ．
(1)、若∠ABC=60°，∠ACB=40°，求∠A和∠D的度数．(2)、由⑴小题的计算结果，猜想，∠A和∠D有什么数量关系，并加以证明．24. 在中， ， ， ， D为上一点，连接 ， 过点C作于点E．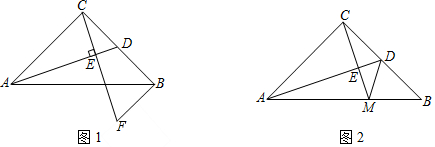
(1)、如图1，过点B作交的延长线于点F，求证：；(2)、如图2，若D为的中点，的延长线交于点M，连接 ． 求证：；25. 如图1，有平面直角坐标系中，A(-2，0)，B(0，3），C(3、0)，D(0，2）
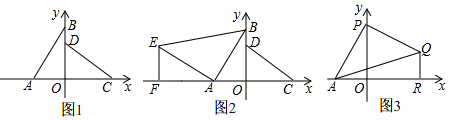(1)、求证：AB=CD且AB⊥CD；(2)、如图2，以A为直角顶点在第二象限内作等腰直角三角形ABE，过点E作EF⊥x轴于点F，求点F的坐标；(3)、如图3，若点P为y轴正半轴上一动点，以AP为直角边作等腰直角三角形APQ，点Q在第一象限，∠APQ=90°，QR⊥x轴于点R，当点P运动时，OP-QR的值是否发生变化?若不变，求出其值；若变化，请说明理由．