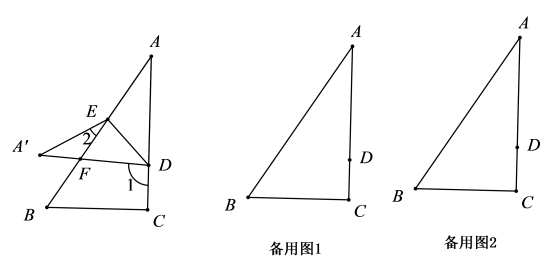河南省焦作武陟县城区2021-2022学年八年级上学期阶段评估(一)数学试题
试卷更新日期:2022-09-06 类型:月考试卷
一、单选题
-
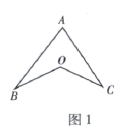
1. 如图,在中,边上的高是( )
 A、 B、 C、BF D、2. 下列各选项中的两个图形属于全等形的是( )A、
A、 B、 C、BF D、2. 下列各选项中的两个图形属于全等形的是( )A、 B、
B、 C、
C、 D、
D、 3. 多边形的边数由3增加到2021时,其外角和的度数( )A、增加 B、减少 C、不变 D、不能确定4. 要使如图所示的六边形木架不变形,则至少需要钉上木条的根数为( )
3. 多边形的边数由3增加到2021时,其外角和的度数( )A、增加 B、减少 C、不变 D、不能确定4. 要使如图所示的六边形木架不变形,则至少需要钉上木条的根数为( ) A、1 B、2 C、3 D、45. 如图,李老师用长方形纸板遮住了的一部分,其中 , 则另外两边的长不可能是( )
A、1 B、2 C、3 D、45. 如图,李老师用长方形纸板遮住了的一部分,其中 , 则另外两边的长不可能是( )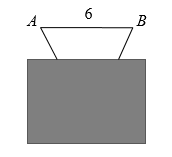 A、3,4 B、2,5 C、3,6 D、2,36. 如图, , 垂足为 , , , 则的大小为( )
A、3,4 B、2,5 C、3,6 D、2,36. 如图, , 垂足为 , , , 则的大小为( )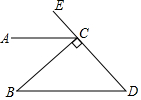 A、50° B、40° C、55° D、60°7. “花影遮墙,峰峦叠窗”苏州园林空透的窗棂中蕴含着许多的数学元素.如图是窗棂是冰裂纹窗及这种窗棂中的部分图案.若 , , 则下列判断中正确的是( )
A、50° B、40° C、55° D、60°7. “花影遮墙,峰峦叠窗”苏州园林空透的窗棂中蕴含着许多的数学元素.如图是窗棂是冰裂纹窗及这种窗棂中的部分图案.若 , , 则下列判断中正确的是( )
 A、 B、 C、 D、的度数无法确定8. 如图,在中,、的三等分线交于点、 , 若 , 则的度数为( )
A、 B、 C、 D、的度数无法确定8. 如图,在中,、的三等分线交于点、 , 若 , 则的度数为( ) A、135° B、125° C、145° D、120°9. 如图,在中, , 分别以 , 为边,向外作正方形和正五边形 , 则的大小为( )
A、135° B、125° C、145° D、120°9. 如图,在中, , 分别以 , 为边,向外作正方形和正五边形 , 则的大小为( ) A、32° B、42° C、52° D、48°10. 如图,交于点 , 的平分线与的外角的平分线交于点 , , 则下列说法不正确的是(
A、32° B、42° C、52° D、48°10. 如图,交于点 , 的平分线与的外角的平分线交于点 , , 则下列说法不正确的是(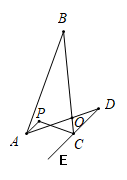 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
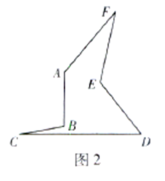
11. 图中以为边的三角形共有个.
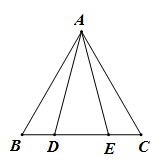 12. 在风筝节活动中,小华用木棒制作了一个风筝,这个风筝可以看作将沿直线翻折,得到(如图所示).若 , , , 则制作这个风筝大约需要木棒的长度为cm.
12. 在风筝节活动中,小华用木棒制作了一个风筝,这个风筝可以看作将沿直线翻折,得到(如图所示).若 , , , 则制作这个风筝大约需要木棒的长度为cm. 13. 如图,在正六边形中,延长 , 交于点 , 则的度数为 .
13. 如图,在正六边形中,延长 , 交于点 , 则的度数为 . 14. 如图,是的边上一点, , , , 则的度数为 .
14. 如图,是的边上一点, , , , 则的度数为 . 15. 如图, , , 分别是三边延长线上的点, , 则°.
15. 如图, , , 分别是三边延长线上的点, , 则°.
三、解答题
-
16.(1)、如图,△ABC≌△DEF,点B、F、C、E在同一条直线上,若BE=10,FC=2,求BF的长.
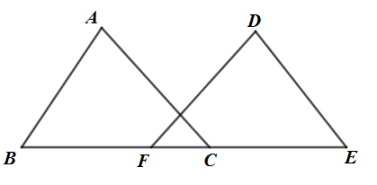 (2)、如图,CE是△ABC外角∠ACD的平分线,∠ACB=40°,∠A=70°,求证:AB//CE.
(2)、如图,CE是△ABC外角∠ACD的平分线,∠ACB=40°,∠A=70°,求证:AB//CE. 17. 如图,在中, , 分别是 , 边上的中线.已知 , , 且的周长为15,边上的高为3.96,求的面积.
17. 如图,在中, , 分别是 , 边上的中线.已知 , , 且的周长为15,边上的高为3.96,求的面积. 18. 已知一个多边形的内角和与外角和的差为1080°.(1)、求这个多边形的边数.(2)、求此多边形的对角线条数.19. 如图, , , 三点在同一直线上,且 ,
18. 已知一个多边形的内角和与外角和的差为1080°.(1)、求这个多边形的边数.(2)、求此多边形的对角线条数.19. 如图, , , 三点在同一直线上,且 ,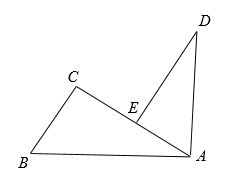 (1)、线段 , , 有怎样的数量关系?请说明理由.(2)、请你猜想满足什么条件时, , 并证明.20. 如图,在四边形中,平分交于点 , 连接 .
(1)、线段 , , 有怎样的数量关系?请说明理由.(2)、请你猜想满足什么条件时, , 并证明.20. 如图,在四边形中,平分交于点 , 连接 . (1)、若 , , , 求的度数.(2)、若 , , 求证: .
(1)、若 , , , 求的度数.(2)、若 , , 求证: .