江苏省盐都区第一共同体2021-2022学年七年级上学期数学第一次自主检测试题

试卷更新日期：2022-09-05 类型：月考试卷

进入出卷网下载

一、单选题

1. 如果收入80元记作 $+ 80$ 元，那么支出 $50$ 元记作（）

A、 $+ 130$ 元 B、 $- 30$ 元 C、 $+ 50$ 元 D、 $- 50$ 元

查看试题解析
2. $- \frac{1}{6}$ 的相反数是（）

A、 $6$ B、 $- 6$ C、 $\frac{1}{6}$ D、 $- \frac{1}{6}$

查看试题解析
3. 如果一个数的平方等于它的倒数，那么这个数一定是（）

A、0 B、1 C、－1 D、1或－1

查看试题解析
4. 在数轴上，一个点从原点开始先向右移动2个单位，再向左移动3个单位后达终点，这个终点表示的数是（）

A、5 B、1 C、 $- 1$ D、 $- 5$

查看试题解析
5. 下列各式正确的是（）.

A、 $- | - 3 | = 3$ B、+(-3)＝3 C、 $- (- 3) = 3$ D、－(-3)＝-3

查看试题解析
6. 所有大于-4.5且小于-1的负整数和为（　　）

A、-7 B、-9 C、-10 D、-14

查看试题解析
7. 如图所示，下列各式正确的是（）

A、 $- a > b$ B、 $a + b > 0$ C、 $a - b > a + b$ D、 $| a | + | b | < | a + b |$

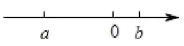查看试题解析
8. 如图在表中填在各正方形中的四个数之间都有相同的规律，根据此规律，m的值是（）

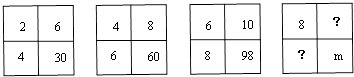A、74 B、104 C、126 D、144

查看试题解析

二、填空题

9. $- 3$ 的绝对值的倒数是．

查看试题解析
10. 数轴上一点A表示的数为﹣5，将点A先向右移2个单位，再向左移10个单位，则这个点表示的数是．

查看试题解析
11. 比较大小： $- \frac{5}{4}$ $- \frac{3}{4}$ （用“>”、“<”、“=”号填空）．

查看试题解析
12. 计算： $| 3.14 - π |$ =（结果保留 $π$ ）．

查看试题解析
13. 月球的半径约为1738000米，1738000这个数用科学记数法表示为．

查看试题解析
14. 如果 $a ， b$ 互为倒数， $c ， d$ 互为相反数，那么 $d - 6 a b + c =$ ．

查看试题解析
15. 若 $| x - 2 | + {(y + 3)}^{2} = 0$ ，则 ${(x + y)}^{2021} =$ .

查看试题解析
16. 已知a、b为有理数，且a＜0,b＞0,a+b＜0,将四个数a、b、－a、－b按从小到大的顺序排列是

查看试题解析
17. 如图所示是计算机某计算程序，若开始输入x=2，则最后输出的结果是．

查看试题解析
18. 如图，圆上有五个点，这五个点将圆分成五等份（每一份称为一段弧长），把这五个点按顺时针方向依次编号为 $1 ， 2 ， 3 ， 4 ， 5$ .若从某一点开始，沿圆周顺时针方向行走，点的编号是数字几，就走几段弧长，我们把这种走法称为一次“移位”.如：小明在编号为3的点，那么他应走3段弧长，即从 $3 \to 4 \to 5 \to 1$ 为第1次“移位”，这时他到达编号为1的点，那么他应走1段弧长，即从 $1 \to 2$ 为第2次“移位”.若小明从编号为4的点开始，第2021次“移位”后，他到达编号为的点.

查看试题解析

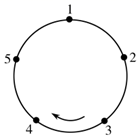
三、解答题

19. 把下列各数填入它所属的集合内：
﹣（﹣2）² ， |﹣ $\frac{3}{4}$ |，0，﹣3.14， $\frac{22}{7}$ ， ﹣12，0.1010010001…，﹣（﹣6），﹣ $\frac{π}{3}$ ．

(1)、无理数集合：{                                 …}

(2)、正数集合：{                                    …}

(3)、非负整数集合：{                                …}

(4)、分数集合：{                                    …}

查看试题解析
20. 计算

(1)、－4－（－4）＋（－3）；

(2)、 $(- 8) + (+ 0.25) - (- 9) + (- \frac{1}{4})$ ；

(3)、 $4 \times {(- 3)}^{} - 5 \times (- 2) + 6$ ；

(4)、 $- 9 \div \frac{5}{9} \times {(- \frac{2}{3})}^{3} \times (- 2^{2})$ ；

(5)、（－ $\frac{1}{6}$ + $\frac{3}{4}$ － $\frac{1}{12}$ ）×（－48）；

(6)、 $(- \frac{1}{30}) \div (\frac{2}{3} - \frac{1}{10} + \frac{1}{6} - \frac{2}{5})$ ．

查看试题解析
21. 在数轴上画出表示 $- 1 \frac{1}{2}$ ， 0，–（–2），–2，–|–3|的点，并用“<”号将所有的数连接起来．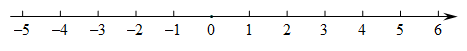

查看试题解析
22. 小明和小亮利用温差来测量山峰的高度，小亮在山脚测得的温度是14℃，此时小明在山顶测得的温度是2℃．已知该地区高度每上升100 m，气温下降0.5℃，求这个山峰的高度．

查看试题解析
23. 某出租车驾驶员从公司出发，在南北向的人民路上连续接送5批客人，行驶路程记录如下（规定向南为正，向北为负，单位：km）：

第1批

第2批

第3批

第4批

第5批

5km

2km

﹣4km

﹣3km

10km

(1)、接送完第5批客人后，该驾驶员在公司的什么方向，距离公司多少千米？

(2)、若该出租车每千米耗油0.1升，那么在这过程中共耗油多少升？

(3)、若该出租车的计价标准为：行驶路程不超过3km收费10元，超过3km的部分按每千米加1.8元收费，在这过程中该驾驶员共收到车费多少元？

查看试题解析
24. 规定符号 $(a ， b)$ 表示 $a$ 、 $b$ 两个数中小的一个，符号 $[a ， b]$ 表示 $a$ 、 $b$ 两个数中大的一个，求下列式子的值．

(1)、填空： $(- 2 ， 4)$ =； $[- 4 ， 2]$ =；

(2)、计算： $（ - 3 ， - 5 ） - [- 8 ， (- 2 ， - 6)]$

查看试题解析
25. 阅读下面材料：点A、B在数轴上分别表示实数a、b，A、B两点之间的距离表示为∣AB∣．当A、B两点中有一点在原点时，不妨设点A在原点，如图1，∣AB∣＝∣OB∣＝∣b∣＝∣a-b∣；当A、B两点都不在原点时，如图2，点A、B都在原点的右边∣AB∣=∣OB∣-∣OA∣=∣b∣-∣a∣= $b - a$ =∣a-b∣；如图3，当点A、B都在原点的左边，∣AB∣＝∣OB∣-∣OA∣＝∣b∣-∣a∣= $- b - (- a)$ =∣a-b∣；如图4，当点A、B在原点的两边，AB∣＝∣OB∣+∣OA∣＝∣a∣+∣b∣= $a + (- b)$ =∣a-b∣．
回答下列问题：

(1)、数轴上表示2和5的两点之间的距离是，数轴上表示1和－3的两点之间的距离是；

(2)、数轴上若点A表示的数是x，点B表示的数是－2，则点A和B之间的距离是，若∣AB∣＝2，那么x为；

(3)、当x是时，代数式 $| x + 2 | + | x - 1 | = 5$ ；

(4)、若点A表示的数，点B与点A的距离是10，且点B在点A的右侧，动点P、Q同时从A、B出发沿数轴正方向运动，点P的速度是每秒3个单位长度，点Q的速度是每秒1个单位长度，求运动几秒后，点P可以追上点Q？（请写出必要的求解过程）

查看试题解析

第1批	第2批	第3批	第4批	第5批
5km	2km	﹣4km	﹣3km	10km