江苏省扬州市江都区邵樊片2021-2022学年七年级上册第一次质量检测数学试题

试卷更新日期：2022-09-05 类型：月考试卷

进入出卷网下载

一、单选题

1. -4的相反数是（）

A、 $\frac{1}{4}$ B、 $- \frac{1}{4}$ C、4 D、-4

查看试题解析
2. 绝对值最小的数（）

A、﹣1 B、0 C、1 D、不存在

查看试题解析
3. 将 $6 - (+ 3) - (- 7) + (- 2)$ 写成省略括号的和的形式为（）

A、 $- 6 - 3 + 7 - 2$ B、 $6 - 3 - 7 - 2$ C、 $6 - 3 + 7 - 2$ D、 $6 + 3 - 7 - 2$

查看试题解析
4. 下面说法中正确的有（）

A、非负数一定是正数 B、有最小的正整数，有最小的正有理数 C、﹣a一定是负数 D、正整数和正分数统称正有理数

查看试题解析
5. 下列正确的是（）

A、 $- \frac{5}{6} < - \frac{4}{5}$ B、 $- (- 21) < + (- 21)$ C、 $- | - 10 \frac{1}{2} | > 8 \frac{2}{3}$ D、 $- | - 7 \frac{2}{3} | = - (- 7 \frac{2}{3})$

查看试题解析
6. 已知a，b两数在数轴上对应的点如图所示，下列结论正确的是（）

A、a+b＞0 B、|a|＞|b| C、ab＜0 D、b﹣a＜0

查看试题解析
7. 已知： $| x |$ =3， $| y |$ =2，且x＞y ，则x+y的值为（）

A、5 B、1 C、5或1 D、－5或－1

查看试题解析
8. 观察下列算式， $2^{1} = 2$ ， $2^{2} = 4$ ， $2^{3} = 8$ ， $2^{4} = 16$ ， $2^{5} = 32$ ， $2^{6} = 64$ ， $2^{7} = 128$ ， $2^{8} = 256$ ，用你所发现的规律得出 $2^{2020}$ 的末位数字是（）

A、2 B、4 C、6 D、8

查看试题解析

二、填空题

9. 立方后为 $- 125$ 的数是．

查看试题解析
10. 月球与地球的平均距离约为384000千米，将数384000用科学记数法表示为.

查看试题解析
11. 南京奥林匹克体育中心位于南京市区西部，占地面积896000平方米，将896000用科学记数法表示为平方米．

查看试题解析
12. 小明写作业时不小心将墨水滴在数轴上，根据图中的数值，判定墨迹盖住部分的整数共有个．

查看试题解析
13. 点A表示数轴上的一个点，将点A向右移动7个单位，再向左移动4个单位，终点恰好是原点，则点A表示的数是.

查看试题解析
14. 规定： $a * b = (a + b) (b + 1)$ 为一种新的运算，则 $2 * (- 5) =$ ．

查看试题解析
15. 若 $| a + 2 | + | b - 4 | = 0$ ，则 $a - b =$ ．

查看试题解析
16. $| x - 3 | + {(y + 2)}^{2} = 0$ ，则 $y^{x}$ 为．

查看试题解析
17. 如图是一个计算程序，当输出值y＝16时，输入值x为．

查看试题解析
18. 如图1，圆的周长为4个单位，在该圆的4等分点处分别标上字母m、n、p、q ，如图2，先让圆周上表示m的点与数轴原点重合，再将数轴按逆时针方向环绕在该圆上，则数轴上表示﹣2018的点与圆周上重合的点对应的字母是．

查看试题解析

三、解答题

19. 把下列各数分别填入相应的集合里： $- | - 3 |$ ， $1.525525552 ⋯$ ， $0$ ， $- (- \frac{3}{4})$ ， $3.14$ ， $- (- 6)$ ， $- \frac{π}{3}$ .
（1）负数集合：{ $⋯$ }；
（2）非负整数集合：{ $⋯$ }；
（3）无理数集合：{ $⋯$ }．

查看试题解析
20. 将下列各数 $- \frac{3}{2}$ ， $0$ ， $- (- 3)$ ， $| - 4 |$ ， $- 2$ ，在数轴上表示出来，并把它们用“ $<$ ”连接起来．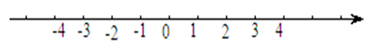

查看试题解析
21. 用简便方法计算：

(1)、 $(- 9) \times 31 \frac{8}{29} - (- 8) \times (- 31 \frac{8}{29}) - (- 16) \times 31 \frac{8}{29}$

(2)、 $99 \frac{71}{72} \times (- 36)$

查看试题解析
22. 一只小虫从某点P出发，在一条直线上来回爬行，假定把向右爬行的路程记为正数，向左爬行的路程记为负数，则爬行各段路程 $($ 单位：厘米 $)$ 依次为：
$+ 5$ ， $- 4$ ， $+ 10$ ， $- 8$ ， $- 7$ ， $+ 14$ ， $- 6$

(1)、通过计算说明小虫是否回到起点P；

(2)、如果小虫爬行的速度为0.6厘米/秒，那么小虫共爬行了多长时间．

查看试题解析
23. 若a与b互为相反数，c与d互为倒数，m的绝对值为4，试求 $\frac{a + b}{m} + c d - m$ 的值；

查看试题解析
24. 已知a、b为有理数，现规定一种新运算，满足a*b=a $\times$ b－a+b

(1)、求2*4的值；

(2)、求（1*3）*（－2）的值．

查看试题解析
25. 外卖员骑摩托车从餐馆出发，先向南骑行 $2 k m$ 到达 $A$ 小区，继续向南骑行 $3 k m$ 到达 $B$ 小区，然后向北骑行 $9 k m$ 到 $C$ 小区，最后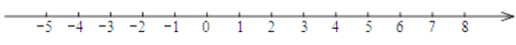回到餐馆．

(1)、以餐馆为原点，以向北方向为正方向，用 $1$ 个单位长度表示 $1 k m$ ，请你在数轴上表示出 $A$ 、 $B$ 、 $C$ 三个小区的位置；

(2)、 $C$ 小区离 $A$ 小区有 $k m$ ．

(3)、若摩托车每 $1 k m$ 耗油 $0.03$ 升，这趟路共耗油多少升？

查看试题解析
26. 点A、B在数轴上分别表示有理数a、b ， A、B两点之间的距离表示为AB ，在数轴上A、B两点之间的距离AB＝|a﹣b|．利用数形结合思想回答下列问题：

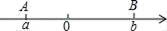(1)、数轴上表示1和3两点之间的距离．

(2)、数轴上表示﹣12和﹣6的两点之间的距离是．

(3)、数轴上表示x和1的两点之间的距离表示为．

(4)、若x表示一个有理数，则|x﹣2|+|x+4|最小值为．

查看试题解析
27. 观察下列各式：1³=1= $\frac{1}{4} \times 1^{2} \times 2^{2}$ ；1³+2³=9= $\frac{1}{4} \times 2^{2} \times 3^{2}$ ；1³+2³+3³=36= $\frac{1}{4} \times 3^{2} \times 4^{2}$ ；1³+2³+3³+4³=100= $\frac{1}{4} \times 4^{2} \times 5^{2} \dots$ ．
回答下面的问题：

(1)、1³+2³+3³+4³+5³+6³= ；

(2)、计算1³+2³+3³+…+9³+10³的值；

(3)、计算：11³+12³+…+19³+20³的值．

查看试题解析
28. 同学们都知道， $| 3 - (- 2) |$ 表示 $3$ 与 $- 2$ 差的绝对值，实际上也可以理解为 $3$ 与 $- 2$ 在数轴上所对应的两个点之间的距离．利用数形结合思想回答下列问题：

(1)、数轴上表示 $2$ 和 $- 8$ 两点之间的距离是．

(2)、 $| 6 - (- 5) | =$ ；若 $| x - 1 | = 3$ ，则 $x =$ ．

(3)、若 $x$ 表示一个有理数， $| x - 1 | + | x + 2 |$ 的最小值为．

(4)、已知数轴上两点 $A$ 、 $B$ 对应的数分别为 $- 1$ ， $3$ ．现点 $A$ 、点 $B$ 分别以 $2$ 个单位长度 $/$ 秒和 $0.5$ 单位长度 $/$ 秒的速度同时向右，当点 $A$ 与点 $B$ 之间的距离为 $3$ 个单位长度时，求点 $A$ 所对应的数是多少？

查看试题解析