山东省临沂市兰陵县2021-2022学年八年级下学期期末数学试题

试卷更新日期：2022-09-02 类型：期末考试

进入出卷网下载

一、单选题

1. 下列根式是最简二次根式的是（）

A、 $\sqrt{\frac{1}{3}}$ B、 $\sqrt{0.3}$ C、 $\sqrt{3}$ D、 $\sqrt{20}$

查看试题解析
2. 下列条件中，不能判断△ABC是直角三角形的是（）

A、a：b：c=3：4：5 B、∠A：∠B：∠C=3：4：5 C、∠A+∠B=∠C D、a：b：c=1：2： $\sqrt{3}$

查看试题解析
3. 在我县“我的中国梦”演讲比赛中，有7名同学参加了比赛，他们最终决赛的成绩各不相同．其中一名学生想要知道自己是否进入前3名，不仅要知道自己的分数，还得知道这7名学生成绩的（）

A、众数 B、方差 C、平均数 D、中位数

查看试题解析
4. 李师傅到单位附近的加油站加油，如图是所用加油机上的显示屏所显示的内容，其中的常量是（）

A、金额 B、数量 C、单价 D、金额和数量

查看试题解析
5. 对于函数 $y = - 3 x + 1$ ，下列结论正确的是（）

A、它的图象必经过点 $(1 ， 3)$ B、y的值随x值的增大而增大 C、当 $x > 0$ 时， $y < 0$ D、它的图象不经过第三象限

查看试题解析
6. 已知 $1 < x < 2$ ，则 $| x - 3 | + \sqrt{{(x - 2)}^{2}}$ 的值为（）

A、 $2 x - 5$ B、－2 C、 $5 - 2 x$ D、2

查看试题解析
7. 如图，四边形ABCD是正方形，△CDE是等边三角形，连接AE，则∠AED的度数为（）

A、10° B、15° C、20° D、30°

查看试题解析
8. 在对一组样本数据进行分析时，小凡列出了方差的计算公式： $s^{2} = \frac{1}{5} [(8 - \bar{x})^{2} + 2 (6 - \bar{x})^{2} + (9 - \bar{x})^{2} + (11 - \bar{x})^{2}]$ ，根据公式不能得到的是（）

A、众数是6 B、方差是6 C、平均数是8 D、中位数是8

查看试题解析
9. 如图，在数轴上，点A，B表示的数分别为0，2，BC⊥AB于点B，且BC＝1.连接AC，在AC上截取CD＝BC，以点A为圆心，AD的长为半径画弧，交线段AB于点E，则点E表示的实数是（）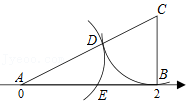

A、2 $\sqrt{5}$ B、 $\sqrt{5}$ +1 C、2 D、 $\sqrt{5}$ ﹣1

查看试题解析
10. 如图，四边形ABCD是萎形，对角线AC、BD相交于点O，DH⊥AB于点H，连接OH，∠CAD＝25°，则∠DHO的度数是（）

A、25° B、30° C、35° D、40°

查看试题解析
11. 一次函数 $y = k x - 2 k$ 的图象经过点 $A$ ，且 $y$ 随 $x$ 的增大而增大，则点 $A$ 的坐标可以是（）

A、 $(1 ， 1)$ B、 $(- 1 ， 3)$ C、 $(0 ， - 1)$ D、 $(3 ， - 1)$

查看试题解析
12. 如图，在矩形ABCD中，点E、F分别在边AB、BC上，且 $A E = \frac{1}{3} A B = 2$ ，将矩形沿直线EF折叠，点B恰好落在AD边上的点P处，连接BP交EF于点Q，下列结论：
① $E F = 2 B E$ ；② $△ A P E$ ≌ $△ Q B E$ ；
③ $F Q = 3 E Q$ ；④ $S_{四边形 B F P E} = 16 \sqrt{3}$ ．
其中正确的结论是（）．

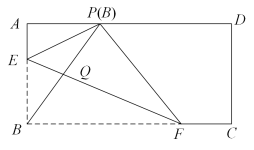A、①②③④ B、①②③ C、②③④ D、①③④

查看试题解析

二、填空题

13. 若 $a = \sqrt{2022} + 1$ ，则 $a^{2} - 2 a + 2$ 的值为．

查看试题解析
14. 如图，在四边形ABCD中，DA⊥AB，DA=AB= $\sqrt{2}$ ，BC= $\sqrt{5}$ ，DC=1．则∠ADC的度数是．

查看试题解析
15. 如图，直线 $y = k x + b$ 分别交x轴、y轴于点A、C，直线 $y = m x + n$ 分别交x轴、y轴于点B、D，直线AC与直线BD相交于点 $M (- 1 ， 2)$ ，则不等式 $k x + b \leq m x + n$ 的解集为．

查看试题解析
16. 如图，在平行四边形OABC中， $A (7 ， 0)$ 、 $C (3 ， 4)$ ，若 $O D = 1$ ，直线l经过D点并且把平行四边形OABC的面积分成相等的两部分，则直线l的解析式是．

查看试题解析

三、解答题

17. 计算

(1)、 $(\sqrt{2} + 3) (\sqrt{2} - 5)$ ；

(2)、 $\sqrt{27} \times \sqrt{\frac{1}{3}} - (\sqrt{5} + \sqrt{3}) (\sqrt{5} - \sqrt{3})$ ．

查看试题解析
18. 为进一步宣传防震减灾科普知识，增强学生应急避险和自救互救能力，某校组织七、八年级各200名学生进行“防震减灾知识测试”（满分100分）．现分别在七，八年级中各随机抽取10名学生的测试成绩x（单位：分）进行统计、整理如下：
七年级：86，90，79，84，74，93，76，81，90，87．
八年级：85，76，90，81，84，92，81，84，83，84．
七八年级测试成绩频数统计表

$70 \leq x < 80$
$80 \leq x < 90$
$90 \leq x \leq 100$
七年级
3
4
3
八年级
1
7
a
七八年级测试成绩分析统计表

平均数
中位数
众数
方差
七年级
84
b
90
36.4
八年级
84
84
c
18.4
根据以上信息，解答下列问题：

(1)、a= ， b= ， c=；

(2)、规定分数不低于85分记为“优秀”，估计这两个年级测试成绩达到“优秀”的学生人数；

(3)、你认为哪个年级的学生掌握防震减灾科普知识的总体水平较好？请说明理由．

查看试题解析
19. 如图，学校要测量旗杆的高度，同学们发现系在旗杆顶端的绳子垂到地面并多出一段（如图1），同学们首先测量了多出的这段绳子长度为1米，再将绳子拉直（如图2），测出绳子末端 $C$ 到旗杆底部 $B$ 的距离为5米，求旗杆的高度．

查看试题解析
20. 如图，平行四边形ABCD的对角线AC，BD相交于点O，E，F分别是OB，OD的中点，连接AE，AF，CE，CF．

(1)、求证：四边形AECF是平行四边形；

(2)、若AB⊥AC，AB＝3，BC＝5．求BD的长．

查看试题解析
21. 如图，直线 $l_{1} ： y = x + 3$ 与过点 $A (3 ， 0)$ 的直线 $l_{2}$ 交于点 $C (1 ， m)$ ，与x轴交于点B．

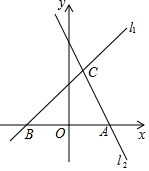(1)、求直线 $l_{2}$ 的解析式；

(2)、点M在直线 $l_{1}$ 上， $M N ∥ y$ 轴，交直线 $l_{2}$ 于点N，若 $M N = 2 A B$ ，请直接写出点M的坐标．

查看试题解析
22. 如图①，四边形ABCD是正方形，点E是BC上一点，连接AE，以AE为一边作正方形AEFG，连接DG．

(1)、求证： $D G = B E$ ；

(2)、如图②，连接AF交CD于点H，连接EH，请探究EH、BE、DH三条线段之间的数量关系，并说明理由．

查看试题解析
23. 受新冠肺炎疫情影响，一水果种植专业户有大量成熟水果无法出售.“一方有难，八方支援”，某水果经销商主动从该种植专业户购进甲、乙两种水果进行销售.专业户为了感谢经销商的援助，对甲种水果的出售价格根据购买量给予优惠，对乙种水果按25元/千克的价格出售.设经销商购进甲种水果 $x$ 千克，付款 $y$ 元， $y$ 与 $x$ 之间的函数关系如图所示.

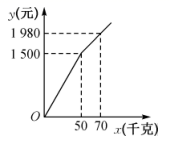(1)、直接写出当 $0 \leq x \leq 50$ 和 $0 > 50$ 时， $y$ 与 $x$ 之间的函数表达式；

(2)、若经销商计划一次性购进甲、乙两种水果共100千克，且甲种水果不少于40千克，但又不超过60千克.如何分配甲、乙两种水果的购进量，才能使经销商付款总金额 $w$ （元）最少？

查看试题解析

	$70 \leq x < 80$	$80 \leq x < 90$	$90 \leq x \leq 100$
七年级	3	4	3
八年级	1	7	a

	平均数	中位数	众数	方差
七年级	84	b	90	36.4
八年级	84	84	c	18.4