山西省朔州市怀仁市2021-2022学年八年级下学期期末数学试题
试卷更新日期:2022-09-02 类型:期末考试
一、单选题
-
1. 一次函数的图象与y轴的交点坐标是( )A、 B、 C、 D、2. 某校为了解学生在校一周体育锻炼时间,随机调查了35名学生,调查结果列表如下:
锻炼时间/h
5
6
7
8
人数
6
15
10
4
则这35名学生在校一周体育锻炼时间的中位数和众数分别为( )
A、6h,6h B、6h,15h C、6.5h,6h D、6.5h,15h3. 对于函数下列结论正确的是( )A、它的图象一定过点 B、它的图象经过第一、二、三象限 C、y的值随x值的增大而增大 D、当时,4. 如图,矩形中,交于点分别为的中点,若 , 则的度数为( ) A、 B、 C、 D、5. 某人匀速跑步到公园,在公园里某处停留了一段时间,再沿原路匀速步行回家,此人离家的距离y与时间x的关系的大致图象是( )A、
A、 B、 C、 D、5. 某人匀速跑步到公园,在公园里某处停留了一段时间,再沿原路匀速步行回家,此人离家的距离y与时间x的关系的大致图象是( )A、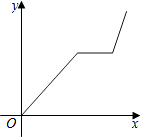 B、
B、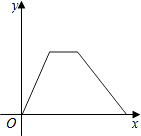 C、
C、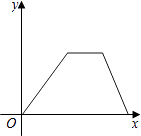 D、
D、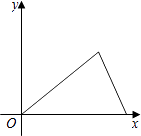 6. 学校举行演讲比赛,共有15名同学进入决赛,比赛将评出金奖1名,银奖3名,铜奖4名,某选手知道自己的分数后,要判断自己能否获奖,他应当关注有关成绩的( )A、平均数 B、中位数 C、众数 D、方差7. 在同一平面直角坐标系中,若一次函数与的图象交于点则点M的坐标为( )A、 B、 C、 D、8. 某店专营某品牌运动鞋,该店老板统计了一周内不同尺码的运动鞋的销售量如图,如果每双鞋的利润相同,你认为该店老板最关注的销售数据是下列统计量中的( )
6. 学校举行演讲比赛,共有15名同学进入决赛,比赛将评出金奖1名,银奖3名,铜奖4名,某选手知道自己的分数后,要判断自己能否获奖,他应当关注有关成绩的( )A、平均数 B、中位数 C、众数 D、方差7. 在同一平面直角坐标系中,若一次函数与的图象交于点则点M的坐标为( )A、 B、 C、 D、8. 某店专营某品牌运动鞋,该店老板统计了一周内不同尺码的运动鞋的销售量如图,如果每双鞋的利润相同,你认为该店老板最关注的销售数据是下列统计量中的( ) A、平均数 B、方差 C、众数 D、中位数9. 一次函数y=kx+b(k,b为常数)的图象如图所示,则不等式kx+b<1的解集是( )
A、平均数 B、方差 C、众数 D、中位数9. 一次函数y=kx+b(k,b为常数)的图象如图所示,则不等式kx+b<1的解集是( ) A、x<﹣2 B、x<1 C、x>﹣2 D、x<010. 如图,在平面直角坐标系中,点B的坐标为 , 将沿轴向右平移后得到点的对应点在直线上,则点A与其对应点之间的距离为( )
A、x<﹣2 B、x<1 C、x>﹣2 D、x<010. 如图,在平面直角坐标系中,点B的坐标为 , 将沿轴向右平移后得到点的对应点在直线上,则点A与其对应点之间的距离为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 代数式有意义,则x的取值范围是 .12. 写出一个图象经过点(1,﹣2)的函数的表达式: .13. 甲、乙两名同学分别进行6次射击训练,训练成绩及平均成绩方差如下表:(单位:环)
第一次
第二次
第三次
第四次
第五次
第六次
平均成绩
方差
甲
9
8
6
7
8
10
8
1.67
乙
8
7
8
9
9
7
8
0.67
甲和乙的训练成绩比较稳定的是 .
14. 如图,两条直线l1和l2的关系式分别为y1=k1x+b1 , y2=k2x+b2 , 两直线的交点坐标为(2,1),当y1>y2时,x的取值范围为.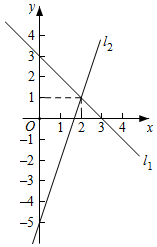 15. 数学老师计算同学们一学期的平均成绩时,将平时、期中和期末的成绩按3:3:4计算,若小红平时、期中和期末的成绩分别是90分、100分、90分,则小红一学期的数学平均成绩是分.16. 如图所示,点A(﹣3,4)在一次函数y=﹣3x+b的图象上,该一次函数的图象与y轴的交点为B,那么△AOB的面积为 .
15. 数学老师计算同学们一学期的平均成绩时,将平时、期中和期末的成绩按3:3:4计算,若小红平时、期中和期末的成绩分别是90分、100分、90分,则小红一学期的数学平均成绩是分.16. 如图所示,点A(﹣3,4)在一次函数y=﹣3x+b的图象上,该一次函数的图象与y轴的交点为B,那么△AOB的面积为 .
三、解答题
-
17. 计算题:(1)、(2)、18. 某校实行学案式教学,需印制若干份数学学案,印刷厂有甲、乙两种.收费方式,除按印刷份数收取印刷费外,甲种方式还需收取制版费而乙种不需要,两种印刷方式的收费费用y(元)与印刷份数x(份)之间的函数关系如图所示:
 (1)、填空:甲种收费方式的函数关系式是 , 乙种收费方式的函数关系式是;(直接写出答案,不写过程)(2)、根据函数图象,请直接写出如何根据每次印刷份数选择省钱的收费方式.(3)、填空:该校八年级每次需印刷800份学案,选择种印刷方式较合算?(填“甲”“乙”,直接写出答案,不写过程)19. 新型冠状病毒的传染性非常强.“戴口罩,勤洗手,多通风”是必要的防护措施.新冠疫情以来,各学校都新增了洗手设备,我市某学校的洗手房一角,水龙头上面的墙壁上还张贴了“七步洗手法”的标语.在洗手的过程中,经常有学生关闭不严水龙头造成滴水,为了增强学生的节水意识,数学兴趣小组进行了漏水量与漏水时间的关系调查研究,在滴水的水龙头下放置一个量筒,每5分钟记录一次水量,如下表.
(1)、填空:甲种收费方式的函数关系式是 , 乙种收费方式的函数关系式是;(直接写出答案,不写过程)(2)、根据函数图象,请直接写出如何根据每次印刷份数选择省钱的收费方式.(3)、填空:该校八年级每次需印刷800份学案,选择种印刷方式较合算?(填“甲”“乙”,直接写出答案,不写过程)19. 新型冠状病毒的传染性非常强.“戴口罩,勤洗手,多通风”是必要的防护措施.新冠疫情以来,各学校都新增了洗手设备,我市某学校的洗手房一角,水龙头上面的墙壁上还张贴了“七步洗手法”的标语.在洗手的过程中,经常有学生关闭不严水龙头造成滴水,为了增强学生的节水意识,数学兴趣小组进行了漏水量与漏水时间的关系调查研究,在滴水的水龙头下放置一个量筒,每5分钟记录一次水量,如下表.时间
0
5
10
15
20
25
30
水量
0
1.5
3
4.5
6
8.5
9
(1)、兴趣小组通过分析上表中的数据发现漏水量与漏水时间存在一种特殊的函数关系,并发现有一组水量记录错了,上表中记录错误的数值是 , 这个数值修改正确应该是;请你直接写出漏水量w关于漏水时间的函数关系式;(2)、该学校有6个洗手房,每个洗手房有10个水龙头,假设每个水龙头都没有关严,且每个水龙头滴水速度都与上表中的速度相同,请你估计该学校一天(24小时)的漏水量;(3)、为了增强学生的节水意识,请你帮兴趣小组写一句提醒学生关紧水龙头的提示语: .20. 阅读理解题在平面直角坐标系 中,点 到直线 的距离公式为: ,
例如,求点 到直线 的距离.
解:由直线 知:
所以 到直线 的距离为:
根据以上材料,解决下列问题:
(1)、求点 到直线 的距离.(2)、若点 到直线 的距离为 ,求实数 的值.21. 6月的第三个星期天是父亲节,某校组织了以“父爱如山”为主题的演讲比赛,根据初赛成绩,七、八年级各选出名学生组成代表队,参加决赛.并根据他们的决赛成绩绘制了如下两幅统计图表:(满分为分)
 (1)、补全下表中的数据;
(1)、补全下表中的数据;组别
平均数(分)
中位数(分)
众数(分)
七年级
八年级
(2)、结合两队决赛成绩的平均数和中位数,评价两个队的决赛成绩;(3)、哪个年级代表队的决赛成绩更稳定.22. 阅读理解阅读下列材料,完成相应任务.
直角三角形斜边上的中线等于斜边的一半
如图1,△ABC中,∠ABC=90°,BD是斜边AC上的中线.求证:BD=AC.
分析:要证明BD等于AC的一半.可以用“倍长法”将BD延长一倍,如图2,延长BD到E,使得DE=BD.连接AE,CE.可证四边形ABCE是矩形,由矩形的对角线相等得BE=AC,这样将直角三角形斜边上的中线与斜边的数量关系转化为矩形对角线的数量关系,进而得到BD=AC.
 (1)、任务一:请你按材料中的分析写出证明过程;(2)、任务二:上述证明方法中主要体现的数学思想是____;A、转化思想 B、类比思想 C、数形结合思想 D、从一般到特殊思想(3)、任务三:如图3,点C是线段AB上一点,CD⊥AB,点E是线段CD的中点,分别连接AD、BE,点F,G分别是AD和BE的中点,连接FG.若AB=12,AC=CD=8,则FG= .23. 综合与探究
(1)、任务一:请你按材料中的分析写出证明过程;(2)、任务二:上述证明方法中主要体现的数学思想是____;A、转化思想 B、类比思想 C、数形结合思想 D、从一般到特殊思想(3)、任务三:如图3,点C是线段AB上一点,CD⊥AB,点E是线段CD的中点,分别连接AD、BE,点F,G分别是AD和BE的中点,连接FG.若AB=12,AC=CD=8,则FG= .23. 综合与探究如图1,直线AB与坐标轴交于A,B两点,已知点A的坐标为(0,3),点B的坐标为(4,0),点C是线段AB上一点.
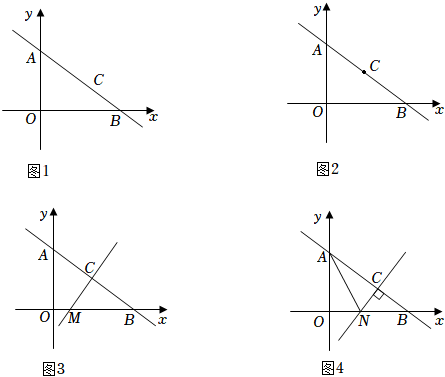 (1)、知识初探:如图1,求直线AB的解析式.(2)、探究计算:如图2,若点C是线段AB的中点,则点C的坐标为(3)、拓展探究:如图3,若点C是线段AB的中点,过点C作线段AB的垂线,交x轴于点M,求点M的坐标.(4)、类比探究:如图4,过点C作线段AB的垂线,交x轴于点N,连接AN,当∠OAN=∠CAN时,则点N的坐标为
(1)、知识初探:如图1,求直线AB的解析式.(2)、探究计算:如图2,若点C是线段AB的中点,则点C的坐标为(3)、拓展探究:如图3,若点C是线段AB的中点,过点C作线段AB的垂线,交x轴于点M,求点M的坐标.(4)、类比探究:如图4,过点C作线段AB的垂线,交x轴于点N,连接AN,当∠OAN=∠CAN时,则点N的坐标为