山东省日照市东港区2021-2022学年八年级下学期期末数学试题
试卷更新日期:2022-09-02 类型:期末考试
一、单选题
-
1. 下列二次根式中是最简二次根式的是( ).A、 B、 C、 D、2. 下列曲线中不能表示y是x的函数的是( )A、
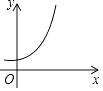 B、
B、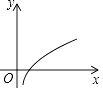 C、
C、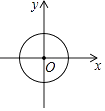 D、
D、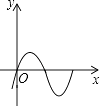 3. 甲、乙、丙、丁四位同学都参加了5次数学模拟测试,每个人这5次成绩的平均数都是125分,方差分别是 , 则这5次测试成绩最稳定的是( )A、甲 B、乙 C、丙 D、丁4. 下列各组数中能作为直角三角形的三边长的是( )A、1,2,3 B、 , , C、4,5, D、6,8,125. 在四边形 中,对角线 , 相交于点 ,则下列说法正确的是( )A、如果 , ,那么四边形 是平行四边形 B、如果 , ,那么四边形 是矩形 C、如果 , ,那么四边形 是菱形 D、如果 , , , ,那么四边形 是正方形6. 关于一次函数y=-x+1的描述,下列说法正确的是( )A、图象经过点 B、图象经过第一、二、三象限 C、y随x的增大而增大 D、图象与y轴的交点坐标是7. 若关于x的一元二次方程(k﹣1)x2+2x﹣2=0有不相等实数根,则k的取值范围是( )A、k> B、k≥ C、k> 且k≠1 D、k≥ 且k≠18. 在平面直角坐标系xOy中,直线:与直线:的图象如图所示,则关于x的不等式的解集为( )
3. 甲、乙、丙、丁四位同学都参加了5次数学模拟测试,每个人这5次成绩的平均数都是125分,方差分别是 , 则这5次测试成绩最稳定的是( )A、甲 B、乙 C、丙 D、丁4. 下列各组数中能作为直角三角形的三边长的是( )A、1,2,3 B、 , , C、4,5, D、6,8,125. 在四边形 中,对角线 , 相交于点 ,则下列说法正确的是( )A、如果 , ,那么四边形 是平行四边形 B、如果 , ,那么四边形 是矩形 C、如果 , ,那么四边形 是菱形 D、如果 , , , ,那么四边形 是正方形6. 关于一次函数y=-x+1的描述,下列说法正确的是( )A、图象经过点 B、图象经过第一、二、三象限 C、y随x的增大而增大 D、图象与y轴的交点坐标是7. 若关于x的一元二次方程(k﹣1)x2+2x﹣2=0有不相等实数根,则k的取值范围是( )A、k> B、k≥ C、k> 且k≠1 D、k≥ 且k≠18. 在平面直角坐标系xOy中,直线:与直线:的图象如图所示,则关于x的不等式的解集为( )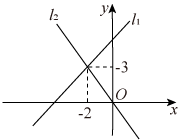 A、 B、 C、 D、9. 如图,在平行四边形中,对角线交于点O,P是的中点.若 , , 则平行四边形的周长为( )
A、 B、 C、 D、9. 如图,在平行四边形中,对角线交于点O,P是的中点.若 , , 则平行四边形的周长为( ) A、12 B、14 C、22 D、2810. 已知点为第四象限内的点,则一次函数的图象大致是( )A、
A、12 B、14 C、22 D、2810. 已知点为第四象限内的点,则一次函数的图象大致是( )A、 B、
B、 C、
C、 D、
D、 11. 如图,菱形ABCD的对角线AC,BD相交于点O,过点D作DH⊥AB于点H,连接OH,若OA=6,OH=4,则菱形ABCD的面积为( )
11. 如图,菱形ABCD的对角线AC,BD相交于点O,过点D作DH⊥AB于点H,连接OH,若OA=6,OH=4,则菱形ABCD的面积为( ) A、24 B、48 C、72 D、9612. 如图,折线ABCDE描述了一辆汽车在某一直线上的行驶过程中,汽车离出发地的距离s(km)与行驶时间t(h)之间的函数关系,根据图中提供的信息,判断下列结论正确的选项是( )
A、24 B、48 C、72 D、9612. 如图,折线ABCDE描述了一辆汽车在某一直线上的行驶过程中,汽车离出发地的距离s(km)与行驶时间t(h)之间的函数关系,根据图中提供的信息,判断下列结论正确的选项是( )
①汽车在行驶途中停留了0.5h;
②汽车在整个行驶过程的平均速度是40km/h;
③汽车共行驶了240km;
④汽车出发4h离出发地40km.
A、①②④ B、①②③ C、①③④ D、①②③④二、填空题
-
13. 代数式在实数范围内有意义,则x的取值范围是 .14. 已知x1 , x2是关于x的方程x2+bx﹣3=0的两根,且满足 ,那么b的值为.15. 如图,在矩形中,两条对角线相交于点O,若 , 则矩形的面积为 .
 16. 在平面直角坐标系中,直线与轴交于点 , 如图所示,依次作正方形 , 正方形 , …,正方形 , 使得点 , , , …在直线上,点 , , , …在y轴正半轴上,则点的坐标为 .
16. 在平面直角坐标系中,直线与轴交于点 , 如图所示,依次作正方形 , 正方形 , …,正方形 , 使得点 , , , …在直线上,点 , , , …在y轴正半轴上,则点的坐标为 .
三、解答题
-
17.(1)、计算:
①;
② .
(2)、解方程:①(公式法)
②(配方法)
18. 为了解某校九年级学生的理化生实验操作情况,随机抽查了若干名学生的实验操作得分(满分为10分),根据获取的样本数据,制作了如图的统计图(1)和图(2),请根据相关信息,解答下列问题: (1)、本次随机抽查的学生人数为 , 在图(2)中,“①”的描述应为“7分”,其中m的值为;(2)、抽取的学生实验操作得分数据的平均数为分,众数为分,中位数为分;(3)、若该校九年级共有1280名学生,估计该校理化生实验操作得满分的学生有多少人?19. 已知关于 的一元二次方程 有两个实数根 和 .(1)、求实数 的取值范围;(2)、当 时,求 的值.20. 在抗疫期间,某药店销售A、B两种类型的口罩,已知销售800只A型口罩和450只B型口罩的利润为2100元,售400只A型口罩和600只B型口罩的利润为1800元.(1)、每只A型口罩和B型口罩的利润分别是多少?(2)、该药店计划一次购进两种型号的口罩共2000只,其中B型口罩的进货量不超过A型口罩的3倍,设购进A型口罩x只,这2000只口罩的利润为y元,问药店购进A、B型口罩各多少才能使销售总利润最大?21. 如图,直线y= x-3分别与x轴,y轴交于点A,B两点,直线y=-x交直线AB于点C,点P从点O出发,以每秒1个单位的速度向点A匀速运动.
(1)、本次随机抽查的学生人数为 , 在图(2)中,“①”的描述应为“7分”,其中m的值为;(2)、抽取的学生实验操作得分数据的平均数为分,众数为分,中位数为分;(3)、若该校九年级共有1280名学生,估计该校理化生实验操作得满分的学生有多少人?19. 已知关于 的一元二次方程 有两个实数根 和 .(1)、求实数 的取值范围;(2)、当 时,求 的值.20. 在抗疫期间,某药店销售A、B两种类型的口罩,已知销售800只A型口罩和450只B型口罩的利润为2100元,售400只A型口罩和600只B型口罩的利润为1800元.(1)、每只A型口罩和B型口罩的利润分别是多少?(2)、该药店计划一次购进两种型号的口罩共2000只,其中B型口罩的进货量不超过A型口罩的3倍,设购进A型口罩x只,这2000只口罩的利润为y元,问药店购进A、B型口罩各多少才能使销售总利润最大?21. 如图,直线y= x-3分别与x轴,y轴交于点A,B两点,直线y=-x交直线AB于点C,点P从点O出发,以每秒1个单位的速度向点A匀速运动. (1)、求点C坐标;(2)、若△COP是等腰三角形,求点P运动时间;(3)、当直线CP平分△OAC的面积时,直线CP与y轴交于点D,求线段CD的长.22. 问题情境:一次数学课上,老师出示了课本中的一道复习题:如图,和都是等边三角形,D、F分别是BC、AB上的点,且 . 连接CF、EF.
(1)、求点C坐标;(2)、若△COP是等腰三角形,求点P运动时间;(3)、当直线CP平分△OAC的面积时,直线CP与y轴交于点D,求线段CD的长.22. 问题情境:一次数学课上,老师出示了课本中的一道复习题:如图,和都是等边三角形,D、F分别是BC、AB上的点,且 . 连接CF、EF. (1)、试判断AD与CF的数量关系,并说明理由;(2)、求证:四边形CDEF是平行四边形.(3)、如图2,四边形ABCD和四边形DEGH都是正方形,F、H分别是AD、AB上的点,且 , 连接CF、EF,试判断四边形CDEF的形状,并说明理由;(4)、 拓展延伸:
(1)、试判断AD与CF的数量关系,并说明理由;(2)、求证:四边形CDEF是平行四边形.(3)、如图2,四边形ABCD和四边形DEGH都是正方形,F、H分别是AD、AB上的点,且 , 连接CF、EF,试判断四边形CDEF的形状,并说明理由;(4)、 拓展延伸:如图3,四边形ABCD和四边形DEGH都是菱形, , , F是AD上一点,连接CF、EF延长H交DC于M,若四边形CDEF是平行四边形,请直接写出AM的长.