山东省济宁市高新区2021-2022学年八年级下学期期末数学试题
试卷更新日期:2022-09-02 类型:期末考试
一、单选题
-
1. 下列根式中,为最简二次根式的是( )A、 B、 C、 D、2. 若代数式有意义,则实数x的取值范围是( )A、 B、 C、 D、且3. 矩形、菱形都具有的性质是( )A、对角线互相垂直 B、对角线相等 C、对角线互相平分 D、对角线垂直、平分且相等4. 若、是方程的两个解,则代数式的值为( )A、8 B、10 C、12 D、145. 已知m是一元二次方程 的一个根,则 2022-m2+m的值为( )A、2019 B、2020 C、2023 D、20256. 如图,在一块长12m,宽8m的矩形空地上,修建同样宽的两条互相垂直的道路(两条道路分别与矩形的一条边平行),剩余部分栽种花草,且栽种花草的面积为 , 设道路的宽为xm,则根据题意,可列方程为( )
 A、 B、 C、 D、7. 有下列四种说法:其中说法正确的有( )
A、 B、 C、 D、7. 有下列四种说法:其中说法正确的有( )①两个菱形相似;②两个矩形相似;③两个平行四边形相似;④两个正方形相似.
A、4个 B、3个 C、2个 D、1个8. 如图,AB∥CD∥EF,AF 与 BE 相交于点 G ,且 DG=2 ,DF=10 , = ,则 AG 的长为( ) A、2 B、3 C、4 D、59. 如图,点P是△ABC的AC边上一点,连接BP,添加下列条件,不能判定△ABC∽△APB的是( )
A、2 B、3 C、4 D、59. 如图,点P是△ABC的AC边上一点,连接BP,添加下列条件,不能判定△ABC∽△APB的是( ) A、∠C=∠ABP B、∠ABC=∠APB C、= D、=10. 将矩形OABC如图放置,O为坐标原点,若点A(﹣1,2),点B的纵坐标是 ,则点C的坐标是( )
A、∠C=∠ABP B、∠ABC=∠APB C、= D、=10. 将矩形OABC如图放置,O为坐标原点,若点A(﹣1,2),点B的纵坐标是 ,则点C的坐标是( )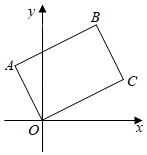 A、(4,2) B、(3, ) C、(3, ) D、(2, )
A、(4,2) B、(3, ) C、(3, ) D、(2, )二、填空题
-
11. 如图,菱形 的对角线 、 相交于点O, ,垂足为E, , ,则 的长为.
 12. 随着新冠疫情趋于缓和,口罩市场趋于饱和,某N95口罩每盒原价为200元,连续两次降价后每盒的售价为72元,则平均每次下降的百分率为 .13. 据《墨经》记载,在两千多年前,我国学者墨子和他的学生做了世界上第1个“小孔成像”的实验,阐释了光的直线传播原理,如图(1)所示。如图(2)所示的小孔成像实验中,若物距为10cm,像距为15cm,蜡烛火焰倒立的像的高度是6cm,则蜡烛火焰的高度是cm.
12. 随着新冠疫情趋于缓和,口罩市场趋于饱和,某N95口罩每盒原价为200元,连续两次降价后每盒的售价为72元,则平均每次下降的百分率为 .13. 据《墨经》记载,在两千多年前,我国学者墨子和他的学生做了世界上第1个“小孔成像”的实验,阐释了光的直线传播原理,如图(1)所示。如图(2)所示的小孔成像实验中,若物距为10cm,像距为15cm,蜡烛火焰倒立的像的高度是6cm,则蜡烛火焰的高度是cm. 14. 图,中,已知点D、E、F分别为BC、AD、CE的中点,设的面积为 , 的面积为 , 则 .
14. 图,中,已知点D、E、F分别为BC、AD、CE的中点,设的面积为 , 的面积为 , 则 . 15. 对于任意的正数a、b定义运算“★”为:a★b= , 则(3★2)×(8★12)的运算结果为 .
15. 对于任意的正数a、b定义运算“★”为:a★b= , 则(3★2)×(8★12)的运算结果为 .三、解答题
-
16. 计算: .17.(1)、解方程:;(2)、解方程 .18. 已知:关于x的方程 .(1)、求证:方程总有实数根;(2)、若方程有一根小于3,求m的取值范围.19. 如图,已知的顶点的坐标分别为 , , .
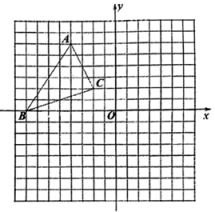 (1)、在第四象限画出关于原点O的位似 , 要求新图形与原图形的位似比为1∶2,并写出点的坐标:(2)、求的面积.20. 如图,点D、E、F分别是△ABC各边的中点,连接DE,EF,AE.
(1)、在第四象限画出关于原点O的位似 , 要求新图形与原图形的位似比为1∶2,并写出点的坐标:(2)、求的面积.20. 如图,点D、E、F分别是△ABC各边的中点,连接DE,EF,AE. (1)、求证:四边形ADEF为平行四边形;(2)、从下列条件①∠BAC=90°;②AE平分∠BAC;③AB=AC中选择一个添加到题干中,使得四边形ADEF为菱形.我选的是(写序号),并证明.21. 某超市销售一种衬衫,平均每天可售出20件,每件盈利40元.为了扩大销售,加盈利,该超市准备适当降价,经过一段时间测算,发现每件衬衫每降低1元,平均每天可多售出2件.(1)、若每件衬衫降价4元时,平均每天可售出多少件衬衫?此时每天销售获利多少元?(2)、在每件盈利不少于25元的前提下,要使该衬衫每天销售获利为1200元,同每件衬衫应降价多少元?(3)、该衬衫每天的销售获利能达到1300元吗?如果能,请写出降价方案,如果不能,请说明理由.22. 如图所示,在矩形ABCD中,AB=12cm,BC=6cm.点P沿AB边从点A开始向点B以2cm/秒的速度移动,点Q沿DA边从点D开始向点A以1cm/秒的速度移动,如果P、Q同时出发,用t(秒)表示移动的时间(0≤t≤6),那么:
(1)、求证:四边形ADEF为平行四边形;(2)、从下列条件①∠BAC=90°;②AE平分∠BAC;③AB=AC中选择一个添加到题干中,使得四边形ADEF为菱形.我选的是(写序号),并证明.21. 某超市销售一种衬衫,平均每天可售出20件,每件盈利40元.为了扩大销售,加盈利,该超市准备适当降价,经过一段时间测算,发现每件衬衫每降低1元,平均每天可多售出2件.(1)、若每件衬衫降价4元时,平均每天可售出多少件衬衫?此时每天销售获利多少元?(2)、在每件盈利不少于25元的前提下,要使该衬衫每天销售获利为1200元,同每件衬衫应降价多少元?(3)、该衬衫每天的销售获利能达到1300元吗?如果能,请写出降价方案,如果不能,请说明理由.22. 如图所示,在矩形ABCD中,AB=12cm,BC=6cm.点P沿AB边从点A开始向点B以2cm/秒的速度移动,点Q沿DA边从点D开始向点A以1cm/秒的速度移动,如果P、Q同时出发,用t(秒)表示移动的时间(0≤t≤6),那么: (1)、点Q运动多少秒时,△APQ的面积为5cm2;(2)、当t为何值时,△QAP与△ABC相似?
(1)、点Q运动多少秒时,△APQ的面积为5cm2;(2)、当t为何值时,△QAP与△ABC相似?