山东省济南市章丘区2021-2022学年八年级下学期期末数学试题
试卷更新日期:2022-09-02 类型:期末考试
一、单选题
-
1. 第24届冬季奥林匹克运动会于2022年2月4日至2月20日在中国北京市和张家口市联合举办,以下是参选的冬奥会会徽设计的部分图形,其中既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 若 , 则下列不等式正确的是( )A、 B、 C、 D、3. 下列由左到右变形,属于因式分解的是( )A、 B、 C、 D、4. 若分式 的值为0,则x的值为( )A、2 B、0 C、﹣2 D、 25. 下列多项式中,在实数范围内不能进行因式分解的是( )A、a2+4 B、a2+2a+1 C、a2-1 D、9a2-6a+16. 一个多边形的每一个内角都是135°,则这个多边形是( )A、七边形 B、八边形 C、九边形 D、十边形7. 下面关于平行四边形的说法中,错误的是( )A、对角线互相平分的四边形是平行四边形 B、有一组对边平行,另一组对边相等的四边形是平行四边形 C、两组对边分别相等的四边形是平行四边形 D、有两组对角相等的四边形是平行四边形8. 如果 是一个完全平方式,那么k是( )
2. 若 , 则下列不等式正确的是( )A、 B、 C、 D、3. 下列由左到右变形,属于因式分解的是( )A、 B、 C、 D、4. 若分式 的值为0,则x的值为( )A、2 B、0 C、﹣2 D、 25. 下列多项式中,在实数范围内不能进行因式分解的是( )A、a2+4 B、a2+2a+1 C、a2-1 D、9a2-6a+16. 一个多边形的每一个内角都是135°,则这个多边形是( )A、七边形 B、八边形 C、九边形 D、十边形7. 下面关于平行四边形的说法中,错误的是( )A、对角线互相平分的四边形是平行四边形 B、有一组对边平行,另一组对边相等的四边形是平行四边形 C、两组对边分别相等的四边形是平行四边形 D、有两组对角相等的四边形是平行四边形8. 如果 是一个完全平方式,那么k是( )
A、6 B、-6 C、 6 D、189. 如图,在 中, , ,AB的垂直平分线交AB于点E,交BC于点F,连接AF,则 的度数( )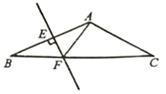 A、 B、 C、 D、10. 已知关于x的分式方程有增根,则k的值是( )A、 B、1 C、2 D、311. 如图,中,平分 , E是中点, , 则的值为( )
A、 B、 C、 D、10. 已知关于x的分式方程有增根,则k的值是( )A、 B、1 C、2 D、311. 如图,中,平分 , E是中点, , 则的值为( )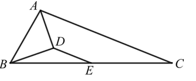 A、 B、 C、 D、12. 已知:四边形ABCD中,AB=2,CD=3,M、N分别是AD,BC的中点,则线段MN的取值范围是( )
A、 B、 C、 D、12. 已知:四边形ABCD中,AB=2,CD=3,M、N分别是AD,BC的中点,则线段MN的取值范围是( ) A、1<MN<5 B、1<MN≤5 C、<MN< D、<MN≤
A、1<MN<5 B、1<MN≤5 C、<MN< D、<MN≤二、填空题
-
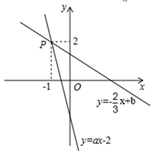
13. 4x2y和6xy2的公因式是 .14. 关于x的不等式组的解集为1<x<3,则a的值为 .15. 如图,已知一次函数y=− x+b和y=ax−2的图象交于点P(−1,2),则根据图象可得不等式− x+b>ax−2的解集是.
 16. 如图,将旋转得到 , DE经过点C,若AD⊥BC,∠B=40°,则∠ACB的度数为 .
16. 如图,将旋转得到 , DE经过点C,若AD⊥BC,∠B=40°,则∠ACB的度数为 .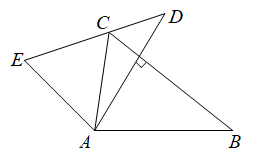 17. 如图,△ABC是边长为1的等边三角形,分别取AC,BC边的中点D,E,连接DE,作得到四边形EDAF,它的周长记作;分别取EF,BE的中点 , , 连接 , 作 , 得到四边形 , 它的周长记作 , 照此规律作下去,则等于 .
17. 如图,△ABC是边长为1的等边三角形,分别取AC,BC边的中点D,E,连接DE,作得到四边形EDAF,它的周长记作;分别取EF,BE的中点 , , 连接 , 作 , 得到四边形 , 它的周长记作 , 照此规律作下去,则等于 .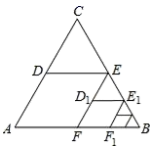
三、解答题
-
18. 分解因式:(1)、4a2-16;(2)、2mx2- 4mxy+2my2 .19. 先化简,再求值:( +1)÷ ,其中a=﹣4.20. 如图,在平面直角坐标系中,ABC三个顶点的坐标分别为A(1,-4),B(5,-4),C(4,-1).
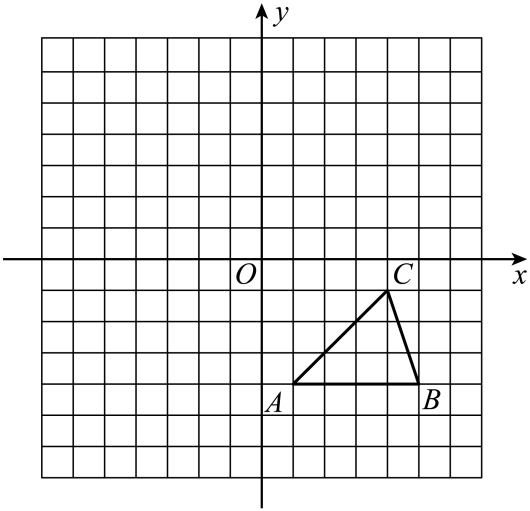 (1)、画出ABC关于原点O成中心对称的A1B1C1;(2)、面出ABC绕点O逆时针旋转90°所得到的A2B2C2;(3)、将ABC先向右平移2个单位长度,再向上平移6个单位长度,画出第二次平移后的A3B3C3 . 若A3B3C3看成是由ABC经过一次平移得到的,则这一平移的距离等于个单位长度.21. 如图,在△ABC中,∠C=90°,点P在AC上运动,点D在AB上运动,PD始终保持与PA相等,BD的垂直平分线交BC于点E,交BD于点F,连接DE.
(1)、画出ABC关于原点O成中心对称的A1B1C1;(2)、面出ABC绕点O逆时针旋转90°所得到的A2B2C2;(3)、将ABC先向右平移2个单位长度,再向上平移6个单位长度,画出第二次平移后的A3B3C3 . 若A3B3C3看成是由ABC经过一次平移得到的,则这一平移的距离等于个单位长度.21. 如图,在△ABC中,∠C=90°,点P在AC上运动,点D在AB上运动,PD始终保持与PA相等,BD的垂直平分线交BC于点E,交BD于点F,连接DE. (1)、判断DE与PD的位置关系,并说明理由;(2)、若AC=3,BC=4,PA=1,则线段DE的长为 .22. 端午节吃粽子是中华民族的传统习俗.某超市节前购进了甲、乙两种畅销口味的粽子.已知购进甲种粽子的金额是1200元,购进乙种粽子的金额是800元,购进甲种粽子的数量比乙种粽子的数量少50个,甲种粽子的单价是乙种粽子单价的2倍.(1)、求甲、乙两种粽子的单价分别是多少元?(2)、为满足消费者需求,该超市准备再次购进甲、乙两种粽子共200个,若总金额不超过1150元,问最多购进多少个甲种粽子?23. 如图,在平行四边形ABCD中,E、F分别是AD、BC边上的点,且 .
(1)、判断DE与PD的位置关系,并说明理由;(2)、若AC=3,BC=4,PA=1,则线段DE的长为 .22. 端午节吃粽子是中华民族的传统习俗.某超市节前购进了甲、乙两种畅销口味的粽子.已知购进甲种粽子的金额是1200元,购进乙种粽子的金额是800元,购进甲种粽子的数量比乙种粽子的数量少50个,甲种粽子的单价是乙种粽子单价的2倍.(1)、求甲、乙两种粽子的单价分别是多少元?(2)、为满足消费者需求,该超市准备再次购进甲、乙两种粽子共200个,若总金额不超过1150元,问最多购进多少个甲种粽子?23. 如图,在平行四边形ABCD中,E、F分别是AD、BC边上的点,且 .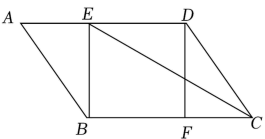 (1)、求证:四边形BEDF是平行四边形;(2)、连接CE,若CE平分∠DCB, , , 求平行四边形ABCD的周长.24. 【阅读材料】
(1)、求证:四边形BEDF是平行四边形;(2)、连接CE,若CE平分∠DCB, , , 求平行四边形ABCD的周长.24. 【阅读材料】把代数式通过配凑等手段,得到局部完全平方式,再进行有关运算和解题,这种解题方法叫做配方法.
如:对于 . (1)用配方法分解因式;(2)当取何值,代数式有最小值?最小值是多少?
解:⑴原式
;
⑵对于 ,
∵ ,
∴当时,代数式有最小值,最小值是 .
【问题解决】利用配方法解决下列问题:
(1)、配方法因式分解:;(2)、当取何值,代数式有最小值?最小值是多少?(3)、对于代数式 , 有最大值还是最小值?请直接写出的最大值或最小值.25. 如图,△ABC是等腰直角三角形,∠ACB=90°,AC=BC=6,D在线段BC上,E是线段AD的一点.现以CE为直角边,C为直角顶点,在CE的下方作等腰直角△ECF , 连接BF .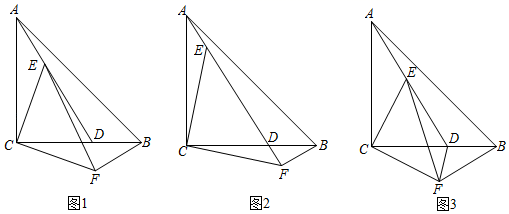 (1)、如图1,求证:AE=BF;(2)、当A、E、F三点共线时,如图2,若BF=2,求AF的长;(3)、如图3,若∠BAD=15°,连接DF , 当E运动到使得∠ACE=30°时,求△DEF的面积.
(1)、如图1,求证:AE=BF;(2)、当A、E、F三点共线时,如图2,若BF=2,求AF的长;(3)、如图3,若∠BAD=15°,连接DF , 当E运动到使得∠ACE=30°时,求△DEF的面积.