山东省济南市天桥区2021-2022学年八年级下学期期末数学试题

试卷更新日期：2022-09-02 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图案中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下面式子从左边到右边的变形是因式分解的是（）

A、x²－x－2＝x(x－1)－2 B、(a＋b)(a－b)＝a²－b² C、x²+3x+2＝(x＋1)(x+2) D、x－2＝x(1－ $\frac{2}{x}$ )

查看试题解析
3. 如图，在平行四边形ABCD中，∠B＝70°，延长CD到点E，则∠1的度数为（）

A、70° B、110° C、80° D、100°

查看试题解析
4. 下列各式是最简分式的是（）

A、 $\frac{12}{6 x}$ B、 $\frac{x - y}{x^{2} - y^{2}}$ C、 $\frac{2 x}{x + 2}$ D、 $\frac{x y}{x^{2}}$

查看试题解析
5. 在平面直角坐标系中，将点（－1，－3）向右平移3个单位长度得到的点的坐标是（）

A、（－4，－3） B、（－1，－6） C、（－1，0） D、（2，－3）

查看试题解析
6. 平行四边形的对角线一定具有的性质是（　　）

A、相等 B、互相平分 C、互相垂直 D、互相垂直且相等

查看试题解析
7. 不等式x－2＞0的解集在数轴上的表示正确的是（）

A、 B、 C、 D、

查看试题解析
8. 正多边形的每一个内角都是120°，那么这个正多边形是（）

A、正五边形 B、正六边形 C、正七边形 D、正八边形

查看试题解析
9. 关于x的一元二次方程x²＋4x＋k＝0有实数根，则k的取值范围是（）

A、k≥4 B、k＜－4 C、k≤4 D、k≤－4

查看试题解析
10. 如图，△AOB中，∠AOB=90°，现在将△AOB绕点O逆时针旋转44°，得到△A'OB'，则∠A'OB的度数为（）

A、44° B、66° C、56° D、46°

查看试题解析
11. 如图，菱形ABCD中，AC＝6，DB＝8，AH⊥BC，则AH等于（）

A、 $\frac{24}{5}$ B、 $\frac{12}{5}$ C、5 D、4

查看试题解析
12. 关于x的一元二次方程方程ax²＋bx＋c＝0（a、b、c均为常数，a≠0）的解是x₁=m-3，x₂=1-m，那么方程a（x-m）²+bx+c=mb的解是（）

A、x₁=3，x₂=1 B、x₁=2m－3，x₂=1 C、x₁=2m－3，x₂=1－2m D、x₁=－3，x₂=1－2m

查看试题解析

二、填空题

13. 分解因式： $x^{2}$ －9= ．

查看试题解析
14. 如图，吴伯伯家有一块等边三角形的空地ABC，已知E，F分别是边AB，AC的中点，量得EF=5米，他想把四边形BCFE用篱笆围成一圈放养小鸡，则需要篱笆的长是米.

查看试题解析
15. 由于受疫情影响，某市高铁站客流量已连续两周下降，由每周50万人次下降至每周32万人次，设平均下降率为x，则根据题意列方程为．

查看试题解析
16. 解关于x的方程 $\frac{x - 3}{x - 1} = \frac{m}{x - 1}$ 产生增根，则常数m的值等于．

查看试题解析
17. 如图， ▱ ABCD中，BE、CF分别平分∠ABC、∠BCD交AD点E、F，已知AB＝3，AD＝5，则EF的长为；

查看试题解析
18. 如图，矩形ABCD中，AB＝4，AD＝3，点E是边BC的中点，连接AE，把△ABE沿AE对折得到△AFE，延长AF与CD交于点G，则DG的长为．

查看试题解析

三、解答题

19. 解不等式组 ${\begin{array}{l} 2 (x + 1) ⩾ x - 1 \\ x + 2 > 3 x - 2 \end{array}$

查看试题解析
20. 先化简，再求值： $(\frac{x}{x - 3} - \frac{1}{3 - x}) \div \frac{x + 1}{x^{2} - 9}$ ，其中 $x = \sqrt{2} - 3$ .

查看试题解析
21. 已知：如图，▱ABCD中，BD是对角线，AE⊥BD于E，CF⊥BD于F．求证：BE＝DF．

查看试题解析
22. 计算

(1)、因式分解：a²b－8ab＋16b

(2)、解方程：x²＋2x－6＝0

查看试题解析
23. 如图，方格纸中每个小正方形的边长都是1个单位长度，在方格纸中建立如图所示的平面直角坐标系．△ABC的顶点都在格点上．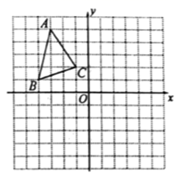

(1)、将△ABC 向右平移 6个单位长度得到△A₁B₁C₁ ，请画出△A₁B₁C₁；

(2)、画出△A₁B₁C₁关于点O的中心对称图形△A₂B₂C₂：

(3)、若将△ABC 绕某一点旋转可得到△A₂B₂C₂ ，请直接写出旋转中心的坐标.

查看试题解析
24. 第二十四届各奥会在我因成功举办，吉祥物“冰墩墩“以其呆萌可爱、英姿队爽形象，深受大家喜爱．某商店购进了甲、乙两种“冰墩墩”玩具，甲种玩具比乙种玩具每件进价低10元；用3000元进价购进的甲种玩具与用3600元购进的乙种玩具数量相同．

(1)、求购进的甲、乙两种玩具，每件的进价各是多少元？

(2)、若计划两种玩具共购进80件，且总价不超过4500元，那么至少购进多少件甲种玩具？

查看试题解析
25. 【阅读理解，自主探究】把代数式通过配凑等手段，得到完全平方式，再运用完全平方式是非负数这一性质增加问题的条件，这种解题方法叫做配方法，配方法在代数式求值，解方程，最值问题等都有着广泛的应用．
例1 用配方法因式分解：a²＋6a＋8．
原式＝ a²＋6a＋9－1＝（a＋3）²－1＝（a＋3－1）（a＋3＋1）＝（a＋2）（a＋4）．
例2若M＝a²－2ab＋2b²－2b＋2，利用配方法求M的最小值；
a²－2ab＋2b²－2b＋2＝a²－2ab＋b²＋b²－2b＋1＋1＝（a－b）²＋（b－1）²＋1；
∵（a－b）²≥0，（b－1）²≥0，
∴当a＝b＝1时，M有最小值1．
请根据上述自主学习材料解决下列问题：

(1)、在横线上添上一个常数项使之成为完全平方式：a²＋10a＋；

(2)、用配方法因式分解：a²－12a＋35．

(3)、若M＝a²－3a+1，则M的最小值为；

(4)、已知a²＋2b²＋c²－2ab＋4b－6c＋13＝0，则a＋b＋c的值为；

查看试题解析
26. 如图，在平面直角坐标系中，AD∥BC，E是BC的中点，BC=12，点A坐标是（0，4），CD所在的直线的函数关系式为y=-x+9，点P是BC上的一个动点．

(1)、点D的坐标为，点E的坐标为；

(2)、当点P在BC边上运动过程中，以点P、A、D、E为顶点的四边形是平行四边形时，求出BP的长；

(3)、在（2）的条件下，请你判断以点P、A、D、E为顶点的四边形能否构成菱形，并说明理由．

查看试题解析
27. 已知四边形ABCD和四边形AEFG均为正方形，连接BE、DG，直线BE与DG交于点H．

(1)、如图1，当E点在AD上时，线段BE与DG的数量关系是；∠BHD的度数为；

(2)、如图2，将正方形AEFG绕点A旋转任意角度，
①请你判断（1）中的结论是否仍然成立，并说明理由；
②当点H在直线AD左侧时，连接AH，则存在实数m、n满足等式：mAH＋DH＝nBH．猜想m、m的值、并证明；

(3)、若AB＝6、AE＝1，则正方形AEFG绕点A旋转的过程中，点F、H是否能重合？若能，请直接写出此时线段BG的长；若不能，请说明理由．

查看试题解析