山东省菏泽市鄄城县2021-2022学年八年级下学期期末数学试题
试卷更新日期:2022-09-02 类型:期末考试
一、单选题
-
1. 下列各式中,属于分式的为( )A、 B、 C、 D、2. 不等式x>2的解集在数轴上表示正确的是( )A、
 B、
B、 C、
C、 D、
D、 3. 如图,在ABCD中,对角线AC,BD交于点O,则下列结论正确的是( )
3. 如图,在ABCD中,对角线AC,BD交于点O,则下列结论正确的是( ) A、AB=CD B、OA=OD C、AD=CD D、AC⊥BD4. 下列各式由左到右的变形中,属于分解因式的是( )A、 B、 C、 D、5. 下列说法错误的是( )A、有一个角是的等腰三角形是等边三角形 B、等腰三角形的角平分线,中线,高相互重合 C、如果一个三角形有两个角相等,那么这两个角所对的边也相等 D、与线段两个端点距离相等的点在这条线段的垂直平分线上6. 若分式 的值等于0,则 的值为( )A、2 B、0 C、 D、7. 如图,在方格纸中,将 绕点 按顺时针方向旋转90°后得到 ,则下列四个图形中正确的是( )
A、AB=CD B、OA=OD C、AD=CD D、AC⊥BD4. 下列各式由左到右的变形中,属于分解因式的是( )A、 B、 C、 D、5. 下列说法错误的是( )A、有一个角是的等腰三角形是等边三角形 B、等腰三角形的角平分线,中线,高相互重合 C、如果一个三角形有两个角相等,那么这两个角所对的边也相等 D、与线段两个端点距离相等的点在这条线段的垂直平分线上6. 若分式 的值等于0,则 的值为( )A、2 B、0 C、 D、7. 如图,在方格纸中,将 绕点 按顺时针方向旋转90°后得到 ,则下列四个图形中正确的是( )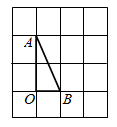 A、
A、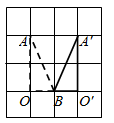 B、
B、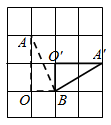 C、
C、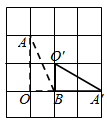 D、
D、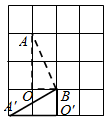 8. 将正六边形与正五边形按如图所示方式摆放,公共顶点为O,且正六边形的边AB与正五边形的边DE在同一条直线上,则∠COF的度数是( )
8. 将正六边形与正五边形按如图所示方式摆放,公共顶点为O,且正六边形的边AB与正五边形的边DE在同一条直线上,则∠COF的度数是( ) A、74° B、76° C、84° D、86°
A、74° B、76° C、84° D、86°二、填空题
-
9. 若一条长为24cm的细线能围成一边长等于9cm的等腰三角形,则该等腰三角形的腰长为cm.10. 若分式有意义,则实数x的取值范围是 .11. 如图,长与宽分别为a、b的长方形,它的周长为16,面积为12,则的值为 .
 12. 如果一个多边形的每个内角都相等,且内角和为1800°,那么该多边形的一个外角是 .13. 如图,一次函数的图象经过点(0,1)和(2,0),则不等式的解集是 .
12. 如果一个多边形的每个内角都相等,且内角和为1800°,那么该多边形的一个外角是 .13. 如图,一次函数的图象经过点(0,1)和(2,0),则不等式的解集是 . 14. 如图,在三角形ABC中,BC=8cm,将三角形ABC以每秒2cm的速度沿BC所在直线向右平移,所得图形对应为三角形DEF,设平移的时间为t秒,当t=时,AD=2CE.
14. 如图,在三角形ABC中,BC=8cm,将三角形ABC以每秒2cm的速度沿BC所在直线向右平移,所得图形对应为三角形DEF,设平移的时间为t秒,当t=时,AD=2CE.
三、解答题
-
15. 因式分解:(1)、;(2)、 .16. 先化简,再求值. , 其中 .17. 如图,已知AB=DC,DE⊥AC,BF⊥AC,垂足分别为 , ,且DE=BF.
求证:四边形 是平行四边形.
 18. 已知在△ABC中,三边长a,b,c满足 a2+2b2+c2−2ab-2bc=0,请判断△ABC的形状,并证明你的结论.19. 如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(﹣3,2),B(﹣4,1),C(﹣2,0).
18. 已知在△ABC中,三边长a,b,c满足 a2+2b2+c2−2ab-2bc=0,请判断△ABC的形状,并证明你的结论.19. 如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(﹣3,2),B(﹣4,1),C(﹣2,0). (1)、若将△ABC向右平移3个单位长度,再向上平移1个单位长度,请画出平移后的△A1B1C1;(2)、若△A2B2C2与△ABC是中心对称图形,则对称中心的坐标为 .20. 若不等式组的解集为-1<x<1,求(a+1)(b-1)的值.21. 为了做好防疫工作,保障员工安全健康,某公司用4000元购进一批某种型号的口罩.由于质量较好,公司又用6400元购进第二批同一型号的口罩,已知第二批口罩的数量是第一批的2倍,且每包便宜5元.问第一批口罩每包的价格是多少元?公司前后两批一共购进多少包口罩?22. 求证:三角形的一条中位线与第三边上的中线互相平分.(要求:先画出图形并写出已知、求证,再写出证明过程)23. 某中学计划暑假期间安排4名老师带领部分学生参加红色旅游.甲、乙两家旅行社的服务质量相同,且报价都是每人元.经协商,甲旅行社的优惠条件是:老师、学生都按八折收费;乙旅行社的优惠条件是:四位老师全额收费,学生都按七折收费.(1)、设参加这次红色旅游的老师和学生共有x名,、单位:元分别表示选择甲、乙两家旅行社所需的费用,求、关于x的关系式.(2)、他们选择哪家旅行社支付的旅游费用较少?24. 如图,已知△ABC是等边三角形,在△ABC外有一点D,连接AD,BD,CD,将△ACD绕点A按顺时针方向旋转得到△ABE,AD与BE交于点F, .
(1)、若将△ABC向右平移3个单位长度,再向上平移1个单位长度,请画出平移后的△A1B1C1;(2)、若△A2B2C2与△ABC是中心对称图形,则对称中心的坐标为 .20. 若不等式组的解集为-1<x<1,求(a+1)(b-1)的值.21. 为了做好防疫工作,保障员工安全健康,某公司用4000元购进一批某种型号的口罩.由于质量较好,公司又用6400元购进第二批同一型号的口罩,已知第二批口罩的数量是第一批的2倍,且每包便宜5元.问第一批口罩每包的价格是多少元?公司前后两批一共购进多少包口罩?22. 求证:三角形的一条中位线与第三边上的中线互相平分.(要求:先画出图形并写出已知、求证,再写出证明过程)23. 某中学计划暑假期间安排4名老师带领部分学生参加红色旅游.甲、乙两家旅行社的服务质量相同,且报价都是每人元.经协商,甲旅行社的优惠条件是:老师、学生都按八折收费;乙旅行社的优惠条件是:四位老师全额收费,学生都按七折收费.(1)、设参加这次红色旅游的老师和学生共有x名,、单位:元分别表示选择甲、乙两家旅行社所需的费用,求、关于x的关系式.(2)、他们选择哪家旅行社支付的旅游费用较少?24. 如图,已知△ABC是等边三角形,在△ABC外有一点D,连接AD,BD,CD,将△ACD绕点A按顺时针方向旋转得到△ABE,AD与BE交于点F, .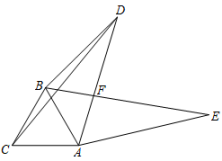 (1)、求的大小;(2)、连接DE,若BD=3,CD=5,求AD的长.
(1)、求的大小;(2)、连接DE,若BD=3,CD=5,求AD的长.