山东省菏泽市单县2021-2022学年八年级下学期期末数学试题
试卷更新日期:2022-09-02 类型:期末考试
一、单选题
-
1. 下列说法中,正确的是( )A、16的平方根是4 B、0.4的算术平方根是0.2 C、64的立方根是 D、-64的立方根是-42. 式子有意义,则的取值范围是( )A、 B、且 C、 D、且3. 已知平行四边形ABCD,下列条件中,不能判定这个平行四边形为矩形的是( )A、∠A=∠B B、∠A=∠C C、AC=BD D、AB⊥BC4. 若 , , ,则a , b , c的大小关系为( )A、 B、 C、 D、5. 已知A、B两地相距600米,甲、乙两人同时从地出发前往B地,所走路程(米)与行驶时间(分)之间的函数关系如图所示,则下列说法中:
①甲每分钟走100米;
②两分钟后乙每分钟走50米;
③甲比乙提前3分钟到达B地,
正确的有( )个.
 A、0 B、1 C、2 D、36. 已知点A(x1 , y1)、B(x2 , y2)在直线y=kx+b(k≠0)上,当x1<x2时,y2>y1 , 且kb>0,则在平面直角坐标系内,它的图象大致是( )A、
A、0 B、1 C、2 D、36. 已知点A(x1 , y1)、B(x2 , y2)在直线y=kx+b(k≠0)上,当x1<x2时,y2>y1 , 且kb>0,则在平面直角坐标系内,它的图象大致是( )A、 B、
B、 C、
C、 D、
D、 7. 不等式的最小整数解为( )A、-5 B、4 C、-2 D、-18. 已知一次函数过点 , 则下列结论正确的是( )A、y随x的增大而增大 B、直线经过二、三、四象限 C、直线过点 D、与坐标轴围成的三角形面积为19. 计算 的结果正确的是( ).A、1 B、 C、5 D、910. 如图,直线与相交于点 , 则关于x的方程的解是( )
7. 不等式的最小整数解为( )A、-5 B、4 C、-2 D、-18. 已知一次函数过点 , 则下列结论正确的是( )A、y随x的增大而增大 B、直线经过二、三、四象限 C、直线过点 D、与坐标轴围成的三角形面积为19. 计算 的结果正确的是( ).A、1 B、 C、5 D、910. 如图,直线与相交于点 , 则关于x的方程的解是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
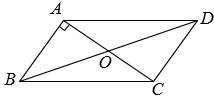
11. 计算: .12. 若点与点关于原点成中心对称,则的值为 .13. 如图,中,对角线AC,BD交于点O, , 若 , , 则BD的长为.
 14. 已知线段AB的A点坐标是(3,2),B点坐标是(-2,-5),将线段AB平移后得到点A的对应点A′的坐标是(5,-1),则点B的对应点B′的坐标是 .15. 已知,实数x满足 , 则x的取值范围是 .16. 如图,在直角坐标系中,菱形的顶点A,B,C在坐标轴上,若点B的坐标为 , , 则点D的坐标为 .
14. 已知线段AB的A点坐标是(3,2),B点坐标是(-2,-5),将线段AB平移后得到点A的对应点A′的坐标是(5,-1),则点B的对应点B′的坐标是 .15. 已知,实数x满足 , 则x的取值范围是 .16. 如图,在直角坐标系中,菱形的顶点A,B,C在坐标轴上,若点B的坐标为 , , 则点D的坐标为 . 17. 若关于x的不等式组无解,则m的取值范围是 .18. 如果a,b都是有理数,且满足 , 则的值为 .19. 如图,已知直线l1:y=﹣2x+4与坐标轴分别交于A、B两点,那么过原点O且将 AOB的面积平分的直线l2的表达式为.
17. 若关于x的不等式组无解,则m的取值范围是 .18. 如果a,b都是有理数,且满足 , 则的值为 .19. 如图,已知直线l1:y=﹣2x+4与坐标轴分别交于A、B两点,那么过原点O且将 AOB的面积平分的直线l2的表达式为. 20. 如图,在 中, , .将 绕点A按顺时针方向旋转至 的位置,点 恰好落在边 的中点处,则 的长为 .
20. 如图,在 中, , .将 绕点A按顺时针方向旋转至 的位置,点 恰好落在边 的中点处,则 的长为 .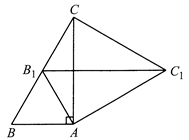
三、解答题
-
21. 计算: .22. 已知方程组中x为非正数,y为负数.(1)、求a的取值范围;(2)、在a的取值范围中,当a为何整数时,不等式的解集为?23. 如图,在四边形ABCD中,AC与BD相交于点O,且AO=CO,点E在BD上,满足∠EAO=∠DCO.
 (1)、求证:四边形AECD是平行四边形;(2)、若AB=BC,CD=5,AC=8,求四边形AECD的面积.24. 如图,在平面直角坐标系中,点O为坐标原点,直线经过 , 两点,点C在直线上,点C的纵坐标为4.
(1)、求证:四边形AECD是平行四边形;(2)、若AB=BC,CD=5,AC=8,求四边形AECD的面积.24. 如图,在平面直角坐标系中,点O为坐标原点,直线经过 , 两点,点C在直线上,点C的纵坐标为4. (1)、求直线的函数表达式及点C的坐标;(2)、若直线的函数表达式为 , 直线的函数表达式为 , 请直接写出满足的的取值范围;(3)、若点D为直线上一动点,且与的面积相等,试求点D的坐标.25. 已知和都是等腰直角三角形, .
(1)、求直线的函数表达式及点C的坐标;(2)、若直线的函数表达式为 , 直线的函数表达式为 , 请直接写出满足的的取值范围;(3)、若点D为直线上一动点,且与的面积相等,试求点D的坐标.25. 已知和都是等腰直角三角形, .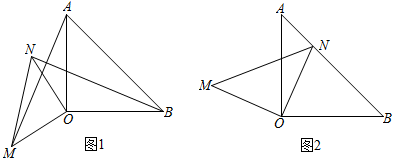 (1)、如图1,连接 , , 求证:和全等:(2)、如图2,将绕点O顺时针旋转,当点N恰好在边上时,求证: .26. 某超市经销甲、乙两种品牌的洗衣液,进货时发现,甲品牌洗衣液每瓶的进价比乙品牌高6元,用1800元购进甲品牌洗衣液的数量是用1800元购进乙品牌洗衣液数量的 . 销售时,甲品牌洗衣液的售价为36元/瓶,乙品牌洗衣液的售价为28元/瓶.(1)、求两种品牌洗衣液的进价;(2)、若超市需要购进甲、乙两种品牌的洗衣液共120瓶,且购进两种洗衣液的总成本不超过3120元,超市应购进甲、乙两种品牌洗衣液各多少瓶,才能在两种洗衣液完全售出后所获利润最大?最大利润是多少元?
(1)、如图1,连接 , , 求证:和全等:(2)、如图2,将绕点O顺时针旋转,当点N恰好在边上时,求证: .26. 某超市经销甲、乙两种品牌的洗衣液,进货时发现,甲品牌洗衣液每瓶的进价比乙品牌高6元,用1800元购进甲品牌洗衣液的数量是用1800元购进乙品牌洗衣液数量的 . 销售时,甲品牌洗衣液的售价为36元/瓶,乙品牌洗衣液的售价为28元/瓶.(1)、求两种品牌洗衣液的进价;(2)、若超市需要购进甲、乙两种品牌的洗衣液共120瓶,且购进两种洗衣液的总成本不超过3120元,超市应购进甲、乙两种品牌洗衣液各多少瓶,才能在两种洗衣液完全售出后所获利润最大?最大利润是多少元?