山东省滨州市博兴县2021-2022学年八年级下学期期末数学试题

试卷更新日期：2022-09-02 类型：期末考试

进入出卷网下载

一、单选题

1. 要使代数式 $\frac{1}{\sqrt{2 x - 1}}$ 在实数范围内有意义，则x的取值范围是（）

A、 $x > \frac{1}{2}$ B、 $x < \frac{1}{2}$ C、 $x \geq \frac{1}{2}$ D、 $x \leq \frac{1}{2}$

查看试题解析
2. 下列运算正确的是（）

A、 $\sqrt{4} + \sqrt{3} = \sqrt{7}$ B、 $\sqrt{4} - \sqrt{3} = 1$ C、 $\sqrt{- 4} \times \sqrt{- 3} = \sqrt{12}$ D、 $\sqrt{9} \div \sqrt{3} = \sqrt{3}$

查看试题解析
3. 以长度分别为下列各组数的线段为边，其中能构成直角三角形的是（）

A、1，2，3 B、2， $\sqrt{2}$ ， $\sqrt{3}$ C、2，1.5，2.5 D、40，50，90

查看试题解析
4. 一元二次方程 $x^{2} = 2 x$ 的解为（）

A、－2 B、2 C、0或－2 D、0或2

查看试题解析
5. 下列说法中，错误的是（）

A、菱形的对角线互相垂直 B、矩形的四个内角都相等 C、对角线互相垂直的四边形是菱形 D、四个内角都相等的四边形是矩形

查看试题解析
6. 下列变量之间关系中，一个变量是另一个变量的正比例函数的是（）

A、正方形的周长C随着边长x的变化而变化 B、正方形的面积S随着边长x的变化而变化 C、面积为20的三角形的一边a随着这边上的高h的变化而变化 D、水箱以0.5L/min的流量往外放水，水箱中的剩水量VL随着放水时间tmin的变化而变化

查看试题解析
7. 关于一次函数 $y = 2 x - 6$ ，下列说法正确的是（）

A、y随x的增大而减小 B、图象交x轴于点 $(0 ， - 6)$ C、点（1，2）在此函数的图象上 D、图象经过第一、三、四象限

查看试题解析
8. 在学校优秀班集体评选中，八年级一班的“学习”、“卫生”、“纪律”、“德育”这四项成绩（百分制）依次为80、84、86、90．若按“学习”成绩占30%、“卫生”成绩占25%、“纪律”成绩占25%、“德育”成绩占20%进行考核打分（百分制），则该班得分为（）

A、81.5 B、84 C、84.5 D、85

查看试题解析
9. 某农科所对甲、乙两种小麦各选用10块面积相同的试验田进行种植试验，它们亩产量的平均数分别是 ${\bar{x}}_{甲} = 621$ 千克， ${\bar{x}}_{乙} = 622$ 千克，方差分别是 $s_{甲}^{2} = 2.6$ ， $s_{乙}^{2} = 28.7$ ．则关于这两种小麦推广种植的合理决策是（）

A、乙的平均亩产量较高，应推广乙 B、甲、乙的平均亩产量相差不多，均可推广 C、甲、乙的平均亩产量相差不多，但甲的亩产量比较稳定，应推广甲 D、乙的平均亩产量较高，且亩产量比较稳定，应推广乙

查看试题解析
10. 如图，图中折线表示张师傅在某天上班途中的情景：骑车离家行了一段路，由于车子出现故障，于是停下修车，修好车子后继续骑行，按时赶到单位．下列关于图中信息的说法中，错误的是（）

A、张师傅修车用了15分钟 B、张师傅的单位距他家2000米 C、张师傅从家到单位共用了20分钟 D、修车后的骑行速度是修车前的2倍

查看试题解析
11. “赵爽弦图”巧妙利用面积关系证明勾股定理，是我国古代数学的骄傲．如图所示的“赵爽弦图”是由四个全等直角三角形和一个小正方形拼成的一个大正方形，若直角三角形较长直角边长为a，较短直角边长为b，且 ${(a + b)}^{2} = 11$ ，小正方形的面积为3，则大正方形的边长为（）

A、10 B、7 C、 $\sqrt{10}$ D、 $\sqrt{7}$

查看试题解析
12. 如图，菱形ABCD的对角线AC、BD相交于点O， $D E ⊥ A B$ 于点E，若 $A B = 5$ ， $D E = 4$ ，则在下列结论中正确的是（）

A、 $D B = 5$ B、 $A E = 4$ C、 $B E = 2$ D、 $O A = 3 \sqrt{2}$

查看试题解析

二、填空题

13. 将 $\sqrt{\frac{1}{3} - \frac{1}{4}}$ 化简成最简二次根式为．

查看试题解析
14. 一元二次方程 $x^{2} - 4 x - 5 = 0$ 的解是：．

查看试题解析
15. “黄金1号”玉米种子的价格为5元/kg．如果一次购买2kg以上的种子，超过2kg部分的种子价格打8折．若王大叔一次付款90元，则能购买到kg的种子．

查看试题解析
16. 如果 $P (- 2 ， m)$ ， $A (3 ， 5)$ ， $B (- 4 ， - 9)$ 三点在同一条直线上，则m的值为．

查看试题解析
17. 已知 $▱ A B C D$ 中， $A B = 6$ ，且AB的长是 $▱ A B C D$ 周长的 $\frac{3}{16}$ ，那么 $B C =$ ．

查看试题解析
18. 如图，在矩形ABCD中，EF为对角线BD的垂直平分线，分别交AD、BC于点E、F，连接AO，若 $A O = 4$ ， $E F = 6$ ，则 $A B =$ ．

查看试题解析

三、解答题

19. 计算：

(1)、 $2 \sqrt{0.5} - (\sqrt{18} - 4 \sqrt{\frac{1}{8}})$ ；

(2)、 $(- \sqrt{2} + 1) (- \sqrt{2} - 1) - {(2 \sqrt{3} - 1)}^{2}$ ．

查看试题解析
20. 省射击队为从甲、乙两名运动员中选拔一人参加全国比赛，对他们进行了六次测试，成绩（单位：环）如下表：
队员
第一次
第二次
第三次
第四次
第五次
第六次
甲
9
10
8
9
8
10
乙
9
9
10
10
7
9

(1)、求甲、乙这六次测试成绩的平均数和方差；

(2)、你认为推荐谁参加全国比赛更合适？请说明理由．

查看试题解析
21. 在一条东西走向河的一侧有一村庄C，河边原有两个取水点A，B，其中AB＝AC，由于种种原因，由C到A的路现在已经不通了，某村为方便村民取水决定在河边新建一个取水点H（A，H，B在一条直线上），并新修一条路CH，测得CB＝3千米，CH＝2.4千米，HB＝1.8千米．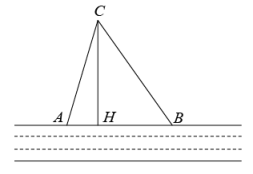

(1)、问CH是不是从村庄C到河边的最近路，请通过计算加以说明；

(2)、求原来的路线AC的长．

查看试题解析
22. 如图，直线 $y = k x + b$ 与x轴交于点 $A (- 5 ， 0)$ ，与y轴交于点B，与直线 $y = \frac{4}{5} x$ 交于点 $C (5 ， m)$ ．若要在y轴找到一个点P使得 $△ B P C$ 的面积为15，求这个点P的坐标．

查看试题解析
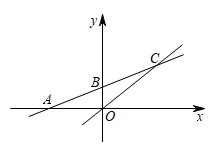23. “冰墩墩”和“雪容融”分别是北京2022年冬奥会和冬残奥会的吉祥物，该吉祥物深受全世界人民的喜爱．经授权，某厂家每天生产两种吉祥物挂件共600件，且当天全部售出，其生产成本及销售单价如下表所示：
吉祥物挂件
生产成本（元/件）
销售单价（元/件）
“冰墩墩”
40
50
“雪容融”
35
43
设该厂每天制作“冰墩墩”挂件x件，每天销售两种吉祥物挂件共获利润为y元．

(1)、求出y与x之间的函数关系式；

(2)、若该厂计划每天投入的总成本不超过22900元，要使得每天所获利润最大，求每天应各生产多少件“冰墩墩”和“雪容融”挂件？并求出最大利润．

查看试题解析
24. 如图，四边形ABCD是正方形，E是边BC上的任意一点， $B F ⊥ A E$ 于点F， $D G ∥ B F$ 交直线AE于点G．

(1)、求证： $D G - B F = G F$ ；

(2)、若 $A B = 4$ ， $B E = 3$ ，求线段GF的长；

(3)、如果将题目改为“E是直线BC上的任意一点”，其它条件均不变，那么（1）所证结论是否仍然成立？若认为仍成立，则简述理由；若认为不一定成立，请直接写出关于DG、BF、GF之间数量关系的正确结论，不必写演推过程．

查看试题解析

队员	第一次	第二次	第三次	第四次	第五次	第六次
甲	9	10	8	9	8	10
乙	9	9	10	10	7	9

吉祥物挂件	生产成本（元/件）	销售单价（元/件）
“冰墩墩”	40	50
“雪容融”	35	43