辽宁省沈阳市浑南区2021-2022学年八年级下学期期末数学试题
试卷更新日期:2022-09-02 类型:期末考试
一、单选题
-
1. 下列分式中,是最简分式的是( ).A、 B、 C、 D、2. 剪纸是中国最古老的民间艺术之一,其在视觉上给人以透空的感觉和艺术享受.下列剪纸作品中既是中心对称图形又是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 已知: , 下列不等式中正确的是( )A、 B、 C、 D、4. 当分式
3. 已知: , 下列不等式中正确的是( )A、 B、 C、 D、4. 当分式 有意义时,x的取值范围是( ) A、x<2 B、x>2 C、x≠2 D、x≥25. 若关于x的分式方程 =1的解为x=2,则m的值为( )A、5 B、4 C、3 D、26. 不等式的解为( )A、 B、 C、 D、7. 下列由左边到右边的变形,是因式分解的是( )A、 B、 C、 D、8. 已知一个n边形的内角和等于外角和的5倍,则n的值为( )A、6 B、8 C、10 D、129. 如图,有A、B、C三个居民点,现要选址建一个新冠疫苗接种点方便居民接种疫苗,要求接种点到三个居民点的距离相等,接种点应建在( )
有意义时,x的取值范围是( ) A、x<2 B、x>2 C、x≠2 D、x≥25. 若关于x的分式方程 =1的解为x=2,则m的值为( )A、5 B、4 C、3 D、26. 不等式的解为( )A、 B、 C、 D、7. 下列由左边到右边的变形,是因式分解的是( )A、 B、 C、 D、8. 已知一个n边形的内角和等于外角和的5倍,则n的值为( )A、6 B、8 C、10 D、129. 如图,有A、B、C三个居民点,现要选址建一个新冠疫苗接种点方便居民接种疫苗,要求接种点到三个居民点的距离相等,接种点应建在( ) A、的三条中线的交点处 B、三边的垂直平分线的交点处 C、三条角平分线的交点处 D、三条高所在直线的交点处10. 已知四边形ABCD中,AB∥CD,添加下列条件仍不能判断四边形ABCD是平行四边形的是( )A、AB=CD B、AD=BC C、AD∥BC D、∠A+∠B=180°
A、的三条中线的交点处 B、三边的垂直平分线的交点处 C、三条角平分线的交点处 D、三条高所在直线的交点处10. 已知四边形ABCD中,AB∥CD,添加下列条件仍不能判断四边形ABCD是平行四边形的是( )A、AB=CD B、AD=BC C、AD∥BC D、∠A+∠B=180°二、填空题
-
11. 在上填上适当的整式: .12. 将点P(2,1)沿x轴方向向左平移3个单位,再沿y轴方向向上平移2个单位,所得的点的坐标是.13. 如图,在中, , , 按以下步骤作图:①以点A为圆心,以任意长为半径作弧,分别交 , 于点M,N;②分别以M,N为圆心,以大于的长为半径作弧,两弧在内交于点O;③作射线 , 交于点D.若 , 则的长为 .
 14. 如图,设k= (a>b>0),则k=.
14. 如图,设k= (a>b>0),则k=.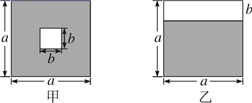 15. 如图,平行四边形的对角线 , 交于点O,平分交于点E, , , 连接 . 下列结论:①;②平分;③;④ , 其中正确的有(写序号即可).
15. 如图,平行四边形的对角线 , 交于点O,平分交于点E, , , 连接 . 下列结论:①;②平分;③;④ , 其中正确的有(写序号即可). 16. 如图,在△ABC中,AD平分∠BAC,交BC于点D,BE⊥AD于E,AB=6,AC=14,∠ABC=3∠C,则BE=.
16. 如图,在△ABC中,AD平分∠BAC,交BC于点D,BE⊥AD于E,AB=6,AC=14,∠ABC=3∠C,则BE=.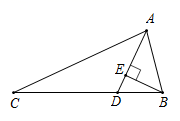
三、解答题
-
17. 把下列各式因式分解:(1)、;(2)、 .18. 解不等式组 ,并写出它的所有整数解.19. 解分式方程: .20. 已知 在平面直角坐标系 内,顶点坐标分别为 , , ,正方形网格中每个小正方形的边长是一个单位长度.

( 1 )画出 向下平移 个单位长度后得到的 ;
( 2 )画出 绕点 顺时针旋转 后得到的 ,并写出点 的坐标;
( 3 )求在(2)中变换过程中,点 绕点 旋转到 点所经过的路径长.
21. 课后,老师在黑板上留了一道练习题,其中部分条件被遮盖已知:如图,E,F是平行四边形对角线上两点,____
求证:四边形是平行四边形.
 (1)、请你从① , ② , , ③中选择一个条件补全命题并证明此命题成立.
(1)、请你从① , ② , , ③中选择一个条件补全命题并证明此命题成立.已知:如图,E,F是平行四边形对角线上两点,( )(填写条件内容)
求证:四边形是平行四边形.
(2)、在(1)中备用的条件中,是否还有可选的条件使命题成立?若有,请直接写出条件,若没有,请说明理由.22. 为保障新冠病毒疫苗接种需求,某生物科技公司开启“加速”模式,生产效率比原先提高了20%,现在生产240万剂疫苗所用的时间比原先生产220万剂疫苗所用的时间少0.5天,问原先每天生产多少万剂疫苗?23. 已知:同一个坐标系中分别作出了一次函数和的图象,分别与x轴交于点A,B,两直线交于点C.已知点 , , 请你观察图象并结合一元一次方程、一元一次不等式和一次函数的相关知识回答下列问题: (1)、关于x的方程的解是;关于x的方程的解是;(2)、关于x的不等式的解集是;(3)、若点 , 请直接写出关于x的不等式的解集;(4)、请直接写出关于x的不等式组的解集.24. 已知:绕点B顺时针旋转得到 , 点A对应点E,点C对应点F,以为边作等边(A,C,D按顺时针排列),连接 , , 设 .
(1)、关于x的方程的解是;关于x的方程的解是;(2)、关于x的不等式的解集是;(3)、若点 , 请直接写出关于x的不等式的解集;(4)、请直接写出关于x的不等式组的解集.24. 已知:绕点B顺时针旋转得到 , 点A对应点E,点C对应点F,以为边作等边(A,C,D按顺时针排列),连接 , , 设 . (1)、如图1所示,若点D,点A在两侧,当时,
(1)、如图1所示,若点D,点A在两侧,当时,①请直接写出的度数;
②用适当的方式表述:线段与之间的关系;所在直线与之间的关系;
(2)、如图2所示,若点D在内部,请判断四边形是否为平行四边形,并证明你的结论.25. 已知:如图1:在中, , , , 在下方作于点D, , 动点E从点A开始沿边以的速度运动,动点F从点C开始沿边以的速度运动.点E和点F同时出发,当点E到达点C时,点F也随之停止运动.设动点E的运动时间为 , 解答下列问题: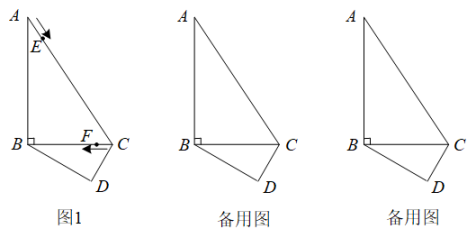 (1)、连接 , 当t为何值时,点C在线段的垂直平分线上;(2)、在运动过程中,是否存在某一时刻t,使是直角三角形?若存在,求出t的值;若不存在,请说明理由;(3)、在(2)的条件下,请直接写出的面积.
(1)、连接 , 当t为何值时,点C在线段的垂直平分线上;(2)、在运动过程中,是否存在某一时刻t,使是直角三角形?若存在,求出t的值;若不存在,请说明理由;(3)、在(2)的条件下,请直接写出的面积.