辽宁省锦州市太和区2019-2020学年八年级下学期期末数学试题

试卷更新日期：2022-09-02 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 使分式 $\frac{x}{x - 3}$ 有意义的条件是（　　）

A、x＝±3 B、x≠±3 C、x≠﹣3 D、x≠3

查看试题解析
3. 下列从左边到右边的变形，属于因式分解的是（）

A、（x+1）（x-1）＝x²-1 B、x²-2x+1＝x（x-2）+1 C、a（x-y）=ax-ay D、x²+2x+1＝（x+1）²

查看试题解析
4. 在▱ABCD中，∠A：∠B=7：2，则∠C的度数是（）.

A、70° B、280° C、140° D、105°

查看试题解析
5. 已知等边三角形的边长为6，则此三角形的面积为（）

A、 $18 \sqrt{3}$ B、 $9 \sqrt{3}$ C、 $6 \sqrt{3}$ D、18

查看试题解析
6. 分式方程 $\frac{x}{x - 2} - 1 = \frac{1}{x^{2} - 4}$ 去分母后的结果正确的是（　　）

A、x²﹣4﹣1＝1 B、x²+2x﹣（x²﹣4）＝1 C、x+2﹣x²﹣4＝1 D、x+2﹣1＝1

查看试题解析
7. 如图，直线 $y = k x + b (k \neq 0)$ 经过点 $(- 2 ， 0)$ ，则不等式 $k x + b > 0$ 的解集为（）

A、 $x > - 2$ B、 $x < - 2$ C、 $x > 0$ D、 $x < 0$

查看试题解析
8. 如图△BAC中，∠C=90°，AD是角平分线，DE⊥AB于E，且BC＝5cm，BD＝3cm，则DE等于（）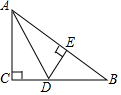

A、2cm B、3cm C、4cm D、5cm

查看试题解析

二、填空题

9. 因式分解：a²b²﹣1＝．

查看试题解析
10. 若分式 $\frac{x}{x - 2}$ 值为0，则实数x的值是．

查看试题解析
11. 将点P（﹣2，﹣3）向右平移5个单位长度得点P′．则点P′的坐标为．

查看试题解析
12. 若一个n边形的外角和与它的内角和之和为1800°，则边数n＝.

查看试题解析
13. 如图，△ABC中，AB＝AC，∠C＝30°，AD⊥AB交BC于点D，若AD＝4，则BC的长为．

查看试题解析
14. 如图，平行四边形ABCD中，EF过对角线的交点O，如果AB＝4 cm，AD＝3 cm，OF＝1 cm，则四边形BCEF的周长为．

查看试题解析
15. 若关于x的分式方程 $\frac{a}{3 - x} + \frac{x}{x - 3} = 2$ 有增根，则a的值．

查看试题解析
16. 若关于x的不等式组 ${\begin{array}{l} x - m \leq 0 \\ 7 - 2 x < 1 \end{array}$ 的整数解共有4个，则m的取值范围是．

查看试题解析

三、解答题

17. 解不等式组 ${\begin{array}{l} x - 3 (x - 2) \geq 4 \\ \frac{1 + 2 x}{3} > x - 1 \end{array}$ ，并把解集在数轴上表示出．

查看试题解析
18. 因式分解：

(1)、3x y²﹣12x；

(2)、x²y﹣2xy²+y³.

查看试题解析
19. 解方程： $\frac{5}{2 x - 1} = \frac{3}{x + 2}$ ．

查看试题解析
20. 先化简，再求值：(x + $\frac{2 x + 1}{x}$ )÷(x+1)，其中x=3.

查看试题解析
21. 如图，已知在直角坐标系中，△ABC的顶点A（﹣1，2），B（﹣3，1），C（0，﹣1）．
( 1 )将△ABC向右平移3个单位得到△DEF，请在图中画出平移后的图形；
( 2 )将△ABC绕点C按逆时针方向旋转90°后得到△MNC，请在图中画出旋转后的图形.

查看试题解析
22. 某单位在疫情期间用3 000元购进A，B两种口罩1 100个，购买A种口罩与购买B种口罩的费用相同，且A种口罩的单价是B种口罩单价的1.2倍；

(1)、求A，B两种口罩的单价各是多少元？

(2)、若计划用不超过7 000元的资金再次购进A，B两种口罩共2 600个，已知A，B两种口罩的进价不变，求A种口罩最多能购进多少个？

查看试题解析
23. 如图，在△ABC中，AB＜AC＜BC，以点A为圆心，线段AB的长为半径画弧，与BC边交于点D，连接AD过点D作DE⊥AD，交AC于点E．

(1)、若∠B＝50°，∠C＝28°，求∠AED度数；

(2)、若点F是BD的中点，连接AF，求证：∠BAF＝∠EDC．

查看试题解析
24. 如图，在等边△ABC中，D，E分别为AB，AC的中点，延长BC至点F，使CF＝ $\frac{1}{2}$ BC，连接CD和EF．

(1)、求证：CD＝EF；

(2)、猜想：△ABC的面积与四边形BDEF的面积的关系，并说明理由．

查看试题解析