江西省宜春市2021-2022学年八年级下学期期末数学试题
试卷更新日期:2022-09-02 类型:期末考试
一、单选题
-
1. 下列二次根式中,是最简二次根式的是( )A、 B、 C、 D、2. 如图,在四边形ABCD中,对角线AC,BD相交于点O,下列条件不能判定这个四边形是平行四边形的是( )
 A、 B、 C、 D、3. 根据疫情防控的要求,学校对所有进入校园的师生进行体温检测,其中7名学生的体温(单位)如下:36.6,36.7,36.6,36.4,36.6,36.5,36.7,这组数据的众数和中位数分别是( )A、36.6,36.4 B、36.6,36.6 C、36.7,36.4 D、36.7,36.64. 在平面直角坐标系中,已知函数y=ax+a(a≠0)的图象过点P(1,2),则该函数的图象可能是( )A、
A、 B、 C、 D、3. 根据疫情防控的要求,学校对所有进入校园的师生进行体温检测,其中7名学生的体温(单位)如下:36.6,36.7,36.6,36.4,36.6,36.5,36.7,这组数据的众数和中位数分别是( )A、36.6,36.4 B、36.6,36.6 C、36.7,36.4 D、36.7,36.64. 在平面直角坐标系中,已知函数y=ax+a(a≠0)的图象过点P(1,2),则该函数的图象可能是( )A、 B、
B、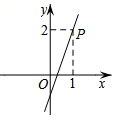 C、
C、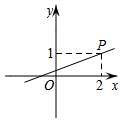 D、
D、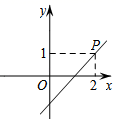 5. 如图,在Rt△ABC中,∠ACB=90°,CD为中线,延长CB至点E,使BE=BC,连结DE,F为DE中点,连结BF.若AC=8,BC=6,则BF的长为( )
5. 如图,在Rt△ABC中,∠ACB=90°,CD为中线,延长CB至点E,使BE=BC,连结DE,F为DE中点,连结BF.若AC=8,BC=6,则BF的长为( )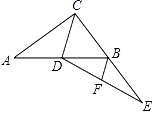 A、2 B、2.5 C、3 D、46. 如图,平行四边形ABCD的对角线AC、BD相交于点O,AE平分∠BAD,分别交BC, BD于点E,P,连接OE, , 则下列结论:①;②;③;④;⑤ . 正确的个数有( )
A、2 B、2.5 C、3 D、46. 如图,平行四边形ABCD的对角线AC、BD相交于点O,AE平分∠BAD,分别交BC, BD于点E,P,连接OE, , 则下列结论:①;②;③;④;⑤ . 正确的个数有( ) A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个二、填空题
-
7. 若二次根式 有意义,则x的取值范围是 .8. 若一次函数的图象经过点 , 则m= .9. 观察分析下列数据,寻找规律:0, , , 3, , …,那么第9个数据是 .10. 如图,一次函数与图象的交点的横坐标为-2,则的解集是 .
 11. 程大位所著《算法统宗》是一部中国传统数学重要的著作.在《算法统宗》中记载:“平地秋千未起,踏板离地一尺.送行二步与人齐,五尺人高曾记.仕女佳人争蹴,终朝笑语欢嬉.良工高士素好奇,算出索长有几?”(1步=5尺).译文:“当秋千静止时,秋干上的踏板离地有1尺高,如将秋千的踏板往前推动两步(10尺)时,踏板就和人一样高,美丽的姑娘和才子们,每天都来争荡秋千,欢声笑语终日不断.好奇的能工巧匠,能算出这秋千的绳索长是多少吗?”如图,假设秋千的绳索长始终保持直线状态,OA是秋千的静止状态,A是踏板,CD是地面,点B是推动两步后踏板的位置,弧AB是踏板移动的轨迹.已知尺,尺,人的身高尺,则尺.
11. 程大位所著《算法统宗》是一部中国传统数学重要的著作.在《算法统宗》中记载:“平地秋千未起,踏板离地一尺.送行二步与人齐,五尺人高曾记.仕女佳人争蹴,终朝笑语欢嬉.良工高士素好奇,算出索长有几?”(1步=5尺).译文:“当秋千静止时,秋干上的踏板离地有1尺高,如将秋千的踏板往前推动两步(10尺)时,踏板就和人一样高,美丽的姑娘和才子们,每天都来争荡秋千,欢声笑语终日不断.好奇的能工巧匠,能算出这秋千的绳索长是多少吗?”如图,假设秋千的绳索长始终保持直线状态,OA是秋千的静止状态,A是踏板,CD是地面,点B是推动两步后踏板的位置,弧AB是踏板移动的轨迹.已知尺,尺,人的身高尺,则尺. 12. 如图,在矩形ABCD中, , 点P在BC上,且 , 以AP为腰作等腰三角形APM,使得点M落在矩形ABCD边上,则 .
12. 如图,在矩形ABCD中, , 点P在BC上,且 , 以AP为腰作等腰三角形APM,使得点M落在矩形ABCD边上,则 .
三、解答题
-
13.(1)、计算:;(2)、如图,在菱形ABCD中,点E,F分别在AB,AD上,且 , 求证: .
 14. 如图,已知 , 求的度数.
14. 如图,已知 , 求的度数. 15. 如图,直线l的解析式为 , 直线l与x轴交于点A,与y轴交于点 , 且 .
15. 如图,直线l的解析式为 , 直线l与x轴交于点A,与y轴交于点 , 且 . (1)、求直线l的解析式:(2)、若点P是直线l上一点, , 求点P的坐标.16. 每年4月23日为世界读书日,某市就初中学生“每天课外阅读”的时间进行随机调查,将调查出现的情况分类:【A类】;【B类】;【C类】;【D类】 . 通过调查,得到下面两幅不完整的统计图,请根据图中的信息解决下面的问题.
(1)、求直线l的解析式:(2)、若点P是直线l上一点, , 求点P的坐标.16. 每年4月23日为世界读书日,某市就初中学生“每天课外阅读”的时间进行随机调查,将调查出现的情况分类:【A类】;【B类】;【C类】;【D类】 . 通过调查,得到下面两幅不完整的统计图,请根据图中的信息解决下面的问题. (1)、在这次随机抽样调查中,共抽查了多少名初中学生?(2)、补全条形统计图,本次调查数据的中位数落在类内;(3)、请你估计该市20000名初中生每天阅读不少于1h的人数.17. 已知四边形ABCD是正方形,是等边三角形,请用无刻度直尺按下列要求画图(保留画图痕迹,不写画法).
(1)、在这次随机抽样调查中,共抽查了多少名初中学生?(2)、补全条形统计图,本次调查数据的中位数落在类内;(3)、请你估计该市20000名初中生每天阅读不少于1h的人数.17. 已知四边形ABCD是正方形,是等边三角形,请用无刻度直尺按下列要求画图(保留画图痕迹,不写画法). (1)、在图1中,画的角平分线;(2)、在图2中,画线段AD的中点.18. 如图,在中,点E是BC边的中点,连接AE并延长与DC的延长线交于点F.
(1)、在图1中,画的角平分线;(2)、在图2中,画线段AD的中点.18. 如图,在中,点E是BC边的中点,连接AE并延长与DC的延长线交于点F. (1)、求证:;(2)、若 , , , 连接DE,求DE的长.19. 第二十四届冬季奥林匹克运动会于2022年2月20日在北京圆满闭幕,目前冰墩墩和雪容融两种奥运吉祥物在市场热销.某特许商店准备购进冰墩墩和雪容融吉祥物若干,其进价和售价如下表所示.已知用3000元购进冰墩墩吉祥物的数量与用2400元购进雪容融吉祥物的数量相同.
(1)、求证:;(2)、若 , , , 连接DE,求DE的长.19. 第二十四届冬季奥林匹克运动会于2022年2月20日在北京圆满闭幕,目前冰墩墩和雪容融两种奥运吉祥物在市场热销.某特许商店准备购进冰墩墩和雪容融吉祥物若干,其进价和售价如下表所示.已知用3000元购进冰墩墩吉祥物的数量与用2400元购进雪容融吉祥物的数量相同.冰墩墩吉祥物
雪容融吉祥物
进价(元/个)
m
售价(元/个)
240
160
(1)、求m的值;(2)、要使购进的两种吉祥物共200个的总利润(利润=售价-进价)不少于21700元,且冰墩墩的个数不超过两种吉祥物总个数的一半,该商店有几种进货方案?(3)、在(2)的条件下,该商店准备对冰墩墩吉祥物每个优惠50元进行出售,雪容融吉祥物的售价不变,该商店怎样进货才能获得最大利润?20. 如图,在平面直角坐标系中,点A,B分别是x轴,y轴上的点,且 , 其中a,b满足 , 将B向右平移18个单位得到点C,动点P从点O出发,沿x轴正方向以每秒2个单位的速度运动,动点Q同时从点B出发,在线段BC上以每秒1个单位的速度向点C运动,当P运动到点A时,点Q也随之停止运动,在运动的过程中PQ与OC的交点是点M,设运动的时间为t秒(). (1)、点A的坐标为;点C的坐标为 .(2)、当四边形CAPQ是平行四边形时,求点M的坐标;(3)、①当时,t=秒;
(1)、点A的坐标为;点C的坐标为 .(2)、当四边形CAPQ是平行四边形时,求点M的坐标;(3)、①当时,t=秒;②当时,t=秒.
21. 如图,点P是正方形ABCD的内部一点,点B关于直线AP的对称点E落在正方形外部,连接BE,DE,AE,其中BE与AP交于点O,延长ED交直线AP于点F,连接BF. (1)、AE和AD的数量关系为;(2)、①若 , 则 ▲ ;
(1)、AE和AD的数量关系为;(2)、①若 , 则 ▲ ;②若 , 求AF;
(3)、若 , 猜想线段AB,FE,FD之间的数量关系,并证明.