江西省上饶市余干县八校联考2021-2022学年八年级下学期期末数学试题

试卷更新日期：2022-09-02 类型：期末考试

进入出卷网下载

一、单选题

1. 下列二次根式中，是最简二次根式的是（）

A、 $\sqrt{15}$ B、 $\sqrt{12}$ C、 $\sqrt{\frac{1}{5}}$ D、 $\sqrt{9}$

查看试题解析
2. 如图，平行四边形ABCD中，若 $∠ A = 60 °$ ，则 $∠ C$ 的度数为（）

A、120° B、60° C、30° D、150°

查看试题解析
3. 我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题：“问有沙田一块，有三斜，其中小斜五里，中斜十二里，大斜十三里，欲知为田几何？”这道题讲的是：有一块三角形沙田，三条边长分别为5里，12里，13里，问这块沙田面积有多大？题中“里”是我国市制长度单位，1里=500米，则该沙田的面积为（）

A、7.5平方千米 B、15平方千米 C、75平方千米 D、750平方千米

查看试题解析
4. 甲、乙、丙、丁四名同学在一次投掷实心球训练中，在相同条件下各投掷10次，他们成绩的平均数 $\bar{x}$ 与方差 $s^{2}$ 如下表：

甲
乙
丙
丁
平均数 $\bar{x}$ （米）
11.1
11.1
10.9
10.9
方差 $s^{2}$
1.1
1.2
1.3
1.4
若要选一名成绩好且发挥稳定的同学参加比赛，则应该选择（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
5. 矩形的边长为 $10 c m$ 和 $15 c m$ ，其中一内角平分线分长边为两部分，这两部分的长为（）

A、 $6 c m$ 和 $9 c m$ B、 $5 c m$ 和 $10 c m$ C、 $4 c m$ 和 $11 c m$ D、 $7 c m$ 和 $8 c m$

查看试题解析
6.
在20km越野赛中，甲乙两选手的行程y（单位：km）随时间x（单位：h）变化的图象如图所示，根据图中提供的信息，有下列说法：①两人相遇前，甲的速度小于乙的速度；②出发后1小时，两人行程均为10km；③出发后1.5小时，甲的行程比乙多3km；④甲比乙先到达终点．其中正确的有（　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

7. 计算 $(\sqrt{6} + \sqrt{3}) (\sqrt{6} - \sqrt{3})$ 的结果等于．

查看试题解析
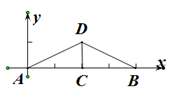
8. 已知y﹣1与x成正比例，当x＝2时，y＝9．那么当y＝﹣15时，x的值为．

查看试题解析
9. 如图，长为8 cm的橡皮筋放置在x轴上，固定两端A和B，然后把中点C向上拉升3 cm到点D，则橡皮筋被拉长了 cm.

查看试题解析
10. 如图，在菱形ABCD中，点A在x轴上，点B的坐标为（4，1），点D的坐标为（0，1），则点C的坐标为．

查看试题解析
11. 某校开展了“书香校园”的活动，小腾班长统计了本学期全班40名同学课外图书的阅读数量（单位：本），绘制了折线统计图（如图所示），在这40名学生的图书阅读数量中，中位数是．

查看试题解析
12. 在矩形ABCD中，AD=5，AB=4，点E，F在直线AD上，且四边形BCFE为菱形．若线段EF的中点为点M，则线段AM的长为 .

查看试题解析

三、解答题

13. 计算：

(1)、 $\sqrt{18} - \sqrt{8} + (\sqrt{3} + 1) (\sqrt{3} - 1)$

(2)、 $\sqrt{12} \times \frac{\sqrt{32}}{3} \div \frac{\sqrt{3}}{3}$

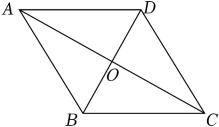
查看试题解析
14. 已知y是x的一次函数，当x=3时，y=1；当x=−2时，y=−4，求这个一次函数的解析式．

查看试题解析
15. 如图，在▱ABCD中，对角线AC与BD交于点O，AC平分∠BAD，AC＝8，BD＝6，求△ABC的周长．

查看试题解析
16. 如图，直线AB与x轴交于点A（1，0），与y轴交于点B（0，﹣2）．

(1)、求直线AB的解析式；

(2)、若直线AB上的点C在第一象限，且S_△_BOC=2，求点C的坐标．

查看试题解析
17. 如图，在正方形 $A B C D$ 中，点 $M$ 是 $B C$ 边上任意一点，请你仅用无刻度的直尺，用连线的方法，分别在图（1）、图（2）中按要求作图（保留作图痕迹，不写作法）.

(1)、在如图（1）的 $A B$ 边上求作一点 $N$ ，连接 $C N$ ，使 $C N = A M$ ；

(2)、在如图（2）的 $A D$ 边上求作一点 $Q$ ，连接 $C Q$ ，使 $C Q ∥ A M$ .

查看试题解析
18. 随着移动互联网的快速发展，基于互联网的共享单车应运而生，为了解某小区居民使用共享单车的情况，某研究小组随机采访该小区的10位居民，得到这10位居民一周内使用共享单车的次数分别为：17，12，15，20，17，0，7，26，17，9．

(1)、这组数据的中位数是，众数是．

(2)、计算这10位居民一周内使用共享单车的平均次数；

(3)、若该小区有200名居民，试估计该小区居民一周内使用共享单车的总次数。

查看试题解析
19. 如图，▱ABCD的对角线AC、BD相交于点O，AE＝CF．

(1)、求证：△BOE≌△DOF；

(2)、连接DE、BF，若BD⊥EF，试探究四边形EBFD的形状，并对结论给予证明．

查看试题解析
20. 同学：你去过黄山吗？在黄山的上山路上，有一些断断续续的台阶，如图8是其中的甲、乙段台阶路的示意图，图8中的数字表示每一级台阶的高度(单位：cm)．并且数d，e，e，c，c，d的方差p，数据b，d，g，f，a，h的方差q，(10cm $<$ a $<$ b $<$ c $<$ d $<$ e $<$ f $<$ g $<$ h $<$ 20cm，且 p $<$ q），请你用所学过的有关统计知识（平均数、中位数、方差和极差）回答下列问题：

(1)、两段台阶路有哪些相同点和不同点？

(2)、哪段台阶路走起来更舒服？为什么？

(3)、为方便游客行走，需要重新整修上山的小路．对于这两段台阶路，在台阶数不变的情况下，请你提出合理的整修建议．

查看试题解析
21. 如图，△ABC中，∠BCA＝90°，CD是边AB上的中线，分别过点C，D作BA和BC的平行线，两线交于点E，且DE交AC于点O，连接AE．

(1)、求证：AD＝CD；

(2)、若∠B＝60°，BC＝3，求四边形ADCE的面积．

查看试题解析
22. 甲、乙两组工人同时加工某种零件，乙组工作中有一次停产更换设备，更换设备后，乙组的工作效率是原来的2倍．两组各自加工零件的数量y(件)与时间x (时)的函数图象如图所示．

(1)、求甲组加工零件的数量y与时间x之间的函数关系式．

(2)、求乙组加工零件总量a的值．

(3)、甲、乙两组加工出的零件合在一起装箱，每够300件装一箱，零件装箱的时间忽略不计，求经过多长时间恰好装满第1箱？再经过多长时间恰好装满第2箱？

查看试题解析
23. 如图1，已知四边形ABCD是正方形，对角线AC、BD相交于点E，以点E为顶点作正方形EFGH．

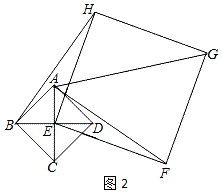
(1)、如图1，点A、D分别在EH和EF上，连接BH、AF，直接写出BH和AF的数量关系；

(2)、将正方形EFGH绕点E顺时针方向旋转．
①如图2，判断BH和AF的数量关系，并说明理由；
②如果四边形ABDH是平行四边形，请在备用图中补全图形；如果四方形ABCD的边长为 $\sqrt{2}$ ，求正方形EFGH的边长．

查看试题解析

	甲	乙	丙	丁
平均数 $\bar{x}$ （米）	11.1	11.1	10.9	10.9
方差 $s^{2}$	1.1	1.2	1.3	1.4