江西省赣州市兴国县2021-2022学年八年级下学期期末检测数学试卷

试卷更新日期：2022-09-02 类型：期末考试

进入出卷网下载

一、单选题

1. 下列式子中，属于最简二次根式的是（）

A、 $\sqrt{9}$ B、 $\sqrt{5}$ C、 $\sqrt{\frac{1}{3}}$ D、 $\sqrt{12}$

查看试题解析
2. 以下列线段a，b，c的长为三边的三角形中，不是直角三角形的是（）

A、 $a = 7$ ， $b = 24$ ， $c = 25$ B、 $a = 1.5$ ， $b = 2$ ， $c = 3$ C、 $a = 1$ ， $b = \sqrt{2}$ ， $c = 1$ D、 $a = 9$ ， $b = 12$ ， $c = 15$

查看试题解析
3. 把直线 $y = - 2 x + 1$ 向下平移3个单位长度后，所得直线的解析式是（）

A、 $y = - 2 x - 2$ B、 $y = - 2 x + 4$ C、 $y = - 2 x - 3$ D、 $y = - 2 x + 3$

查看试题解析
4. 如图，点O是矩形 $A B C D$ 的对角线 $A C$ 的中点，点M是 $A D$ 的中点．若 $A B = 3 ， B C = 4$ ，则四边形 $A B O M$ 的周长是（）

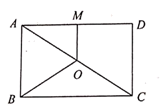A、7 B、8 C、9 D、10

查看试题解析
5. 如图，菱形ABCD的对角线AC、BD的长分别是6cm、8cm，AE⊥BC于点E，则AE的长是（）

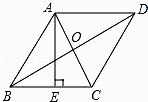A、 $\frac{48}{5}$ cm B、 $\frac{24}{5}$ cm C、 $\frac{12}{5}$ cm D、5 $\sqrt{3}$ cm

查看试题解析
6. 如图，把Rt△ABC放在直角坐标系内，其中∠CAB＝90°，BC＝5，点A，B的坐标分别为（1，0）、（4，0），将△ABC沿x轴向右平移，当点C落在直线y＝2x﹣6上时，线段BC 扫过的面积为（）

A、4 B、5 C、16 D、20

查看试题解析

二、填空题

7. 若二次根式 $\sqrt{x - 2}$ 有意义，则x的取值范围是．

查看试题解析
8. 已知一次函数的函数值 $y$ 随自变量 $x$ 的增大而减小，请写出符合条件的一次函数解析式．（答案不唯一，写出一个即可）

查看试题解析
9. 如图的阴影部分是一个半圆，它的面积是．（结果保留π）

查看试题解析
10. 如图，长为8 cm的橡皮筋放置在x轴上，固定两端A和B，然后把中点C向上拉升3 cm到点D，则橡皮筋被拉长了 cm.

查看试题解析
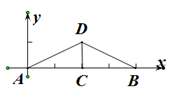11. 如图，将一个边长分别为 8，16 的长方形纸片ABCD折叠，使C点与A点重合，则折痕EF的长是．

查看试题解析
12. 甲、乙两车沿同一平直公路由A地匀速行驶（中途不停留）前往终点B地，甲、乙两车之间的距离y（千米）与甲车行驶时间t（小时）之间的函数关系如图所示，小红通过图像得出以下5个信息：
①甲车速度为45千米/小时；
②A，B两地相距240千米；
③乙车行驶2小时追上甲车；
④乙车由A地到B地共用 $\frac{8}{3}$ 小时；
⑤甲车的速度是乙车速度的 $\frac{3}{4}$ ．
上述信息正确的有．

查看试题解析

三、解答题

13.

(1)、计算： $\sqrt{\frac{1}{3}} \times \sqrt{12} - \sqrt{32} \div \sqrt{2}$

(2)、已知，如图，在四边形ABCD中，∠A=∠C，AB//DC．求证：四边形ABCD是平行四边形．

查看试题解析
14. 如图，甲乙两船从港口A同时出发，甲船沿北偏东38°方向航行，乙船以12海里/时速度沿南偏东52°方向航行，2小时后，甲船到达C岛，乙船到达B岛．若C，B两岛相距40海里，问：甲船的航速是多少？

查看试题解析
15. 已知直线y＝kx+b（k≠0）经过点A（4，0），与直线y＝x﹣2交于点B（3，m）．

(1)、求直线y＝kx+b的函数表达式；

(2)、直接写出不等式kx+b＞x﹣2的解集．

查看试题解析
16. 如图所示，在正方形ABCD中，对角线BD所在的直线上有两点E，F满足BE=DF，连接AE，AF，CE，CF．

(1)、求证：△CBE≌△CDF；

(2)、试判断四边形AECF的形状，并说明理由．

查看试题解析
17. 在图1，图2中，点E是矩形ABCD边AB上的一点，且AE=AD，请仅用无刻度的直尺按下列要求画图（保留画图痕迹，不写画法）．

(1)、在图1中，作∠ADC的角平分线．

(2)、在图2中，作∠ABC的角平分线．

查看试题解析
18. 为缅怀革命先烈，弘扬民族精神，培养学生积极向上的学习情趣，把红色文化引进校园、走进课堂、走入学生的心灵，积极营造红色氛围．某校七年级组织学生参加“红色文化知识竞赛”，从中随机抽取了20份答卷，并统计成绩，（成绩得分用x表示，单位：分）．
收集数据如下：
90，84，86，98，95，95，90，100，89，84，87，89，83，90，93，99，99，97， 92，100
整理数据：
分数范围
$80 \leq x < 85$
$85 \leq x < 90$
$90 \leq x < 95$
$95 \leq x \leq 100$
人数
3
a
b
8
分析数据：
平均分
中位数
众数
92
c
d
根据以上信息，解答下列问题：

(1)、直接写出上述表格中的值：a= ， b= ， c= ， d= ，

(2)、该校七年级有900名学生参加了此次“红色文化知识竞赛”，请估计成绩不低于90分的人数有多少名?

(3)、如果想宣传“红色文化知识”相关知识，你有什么建议？请写出一条即可．

查看试题解析
19. 兴国大乌山成了新的“网红打卡地”，露营看日出日落的绝佳地，大乌胜境，人文铭刻民族风骨．某学校九（1）、九（2）班打算去大乌山研学旅行，负责人准备租用两种型号的帐篷．经市场调查，租用10顶A型帐篷和12顶B型帐篷需要800元，租用25顶A型帐篷和6顶B型帐篷需要1400元．

(1)、求租用每顶A型帐篷和B型帐篷分别需要多少钱；

(2)、根据需要，负责人准备租用两种型号的帐篷共100顶．若租用A型帐篷的顶数不少于B型帐篷顶数的2倍，请设计出最省钱的租用方案，并求出此方案的总费用．

查看试题解析
20. 阅读下列材料，然后回答问题．
在进行二次根式运算时，我们有时会碰上 $\frac{2}{\sqrt{3} + 1}$ 这样的式子，其实我们还可以将其进一步化简：
（Ⅰ） $\frac{2}{\sqrt{3} + 1} = \frac{2 \times (\sqrt{3} - 1)}{(\sqrt{3} + 1) \times (\sqrt{3} - 1)} = \frac{2 \times (\sqrt{3} - 1)}{{(\sqrt{3})}^{2} - 1^{2}} = \sqrt{3} - 1$ ．
以上这种化简的步骤叫作分母有理化．
（Ⅱ） $\frac{2}{\sqrt{3} + 1}$ 还可以用以下方法化简
$\frac{2}{\sqrt{3} + 1} = \frac{3 - 1}{\sqrt{3} + 1} = \frac{（ \sqrt{3} ）^{2} - 1^{2}}{\sqrt{3} + 1} = \frac{（ \sqrt{3} + 1 ） \times （ \sqrt{3} - 1 ）}{\sqrt{3} + 1} = \sqrt{3} - 1$ ．

(1)、请用不同的方法化简 $\frac{2}{\sqrt{5} + \sqrt{3}}$ ．
①参照（Ⅰ）式，化简 $\frac{2}{\sqrt{5} + \sqrt{3}}$ ；
②参照（Ⅱ）式，化简 $\frac{2}{\sqrt{5} + \sqrt{3}}$ ；

(2)、化简： $\frac{1}{\sqrt{3} + \sqrt{1}} + \frac{1}{\sqrt{5} + \sqrt{3}} + \frac{1}{\sqrt{7} + \sqrt{5}} + \dots \dots + \frac{1}{\sqrt{2021} + \sqrt{2019}} + \frac{1}{\sqrt{2023} + \sqrt{2021}}$

查看试题解析
21. 如图所示，在菱形ABCD中，AB=6，∠BAD=120°，点E，F分别在菱形的边BC，CD上滑动，满足∠EAF=60°，连接EF，且E，F不与B，C，D重合．

(1)、求证：不论E，F在BC，CD上如何滑动，总有BE=CF；

(2)、当点E，F在BC，CD上滑动时，分别探讨四边形AECF的面积和△CEF的周长是否发生变化？如果不变，求出这个定值；如果变化，求出最小值．

查看试题解析
22. 已知点A（6，0），点P（x，y）在第一象限内，且满足x+2y=4，设△OPA的面积为S．

(1)、当点P的横坐标为3时，求△OPA的面积．

(2)、用含x的式子表示S，写出x的取值范围，画出函数S的图象．

(3)、若点P的横坐标是纵坐标的2倍，点Q在坐标平面内，请直接写出以O，A，P，Q为顶点的四边形是平行四边形时点Q的坐标．

查看试题解析
23. 如图1，我们把对角线互相垂直的四边形叫做垂美四边形．

(1)、概念理解：在下列四边形中，①正方形；②矩形；③菱形；④平行四边形．是垂美四边形的是：（填写序号）；

(2)、性质探究：如图1，垂美四边形ABCD中，AC⊥BD，垂足为O，试猜想：两组对边AB，CD与BC，AD之间的数量关系，并说明理由；

(3)、问题解决：如图2，分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE，连接CE，BG，GE，且CE与BG相交于点H，已知BC=3，AB=5，求GE长．

查看试题解析

分数范围	$80 \leq x < 85$	$85 \leq x < 90$	$90 \leq x < 95$	$95 \leq x \leq 100$
人数	3	a	b	8

平均分	中位数	众数
92	c	d