江西省赣州市上犹县2021-2022学年八年级下学期期末质量检测数学试题
试卷更新日期:2022-09-02 类型:期末考试
一、单选题
-
1. 计算 的结果是( )A、 B、3 C、 D、92. 下列各组数据中,由线段a,b,c组成的三角形不是直角三角形的一组是( )A、a=6,b=8,c=10 B、a=40,b=50,c=60 C、a= ,b=1,c= D、a= ,b=4,c=53. 某体育用品商店对某一型号运动服9月份的销售情况的统计如图所示,店长决定下个月进该型号运动服时多进一些蓝色的,店长的这一决定主要参考销售数据中的( )
 A、平均数 B、方差 C、中位数 D、众数4. 下列函数中,y随x的增大而减小的函数是( )A、 B、 C、 D、5. 如图,正方形ABCD的对角线AC,BD交于点O,M是边AD上一点,连接OM,过点O作ON⊥OM,交CD于点N.若四边形MOND的面积是1,则AB的长为( )
A、平均数 B、方差 C、中位数 D、众数4. 下列函数中,y随x的增大而减小的函数是( )A、 B、 C、 D、5. 如图,正方形ABCD的对角线AC,BD交于点O,M是边AD上一点,连接OM,过点O作ON⊥OM,交CD于点N.若四边形MOND的面积是1,则AB的长为( ) A、1 B、 C、2 D、6.
A、1 B、 C、2 D、6.小明家、公交车站、学校在一条笔直的公路旁(小明家、学校到这条公路的距离忽略不计),一天,小明从家出发去上学,沿这条公路步行到公交车站恰好乘上一辆公交车,公交车沿这条公路匀速行驶,小明下车时发现还有4分钟上课,于是他沿这条公路跑步赶到学校(上、下车时间忽略不计),小明与家的距离s(单位:米)与他所用时间t(单位:分钟)之间的函数关系如图所示,已知小明从家出发7分钟时与家的距离为1200米,从上公交车到他到达学校共用10分钟,下列说法:
①小明从家出发5分钟时乘上公交车 ②公交车的速度为400米/分钟
③小明下公交车后跑向学校的速度为100米/分钟 ④小明上课没有迟到
其中正确的个数是( )
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
7. 如图,在平行四边形ABCD中,AE平分∠BAD且交BC于点E,∠D=58°,则∠AEC的大小是 .
 8. 要使式子 有意义,则x可取的一个数是 .9. 直线y=3x-6与x轴的交点坐标为 .10. 如图,菱形 的对角线 、 相交于点O, ,垂足为E, , ,则 的长为.
8. 要使式子 有意义,则x可取的一个数是 .9. 直线y=3x-6与x轴的交点坐标为 .10. 如图,菱形 的对角线 、 相交于点O, ,垂足为E, , ,则 的长为. 11. 某人购进一批苹果到集贸市场零售,已知卖出的苹果数量与售价之间的关系如图所示,成本为5元/千克,现以8元/千克卖出,赚元.
11. 某人购进一批苹果到集贸市场零售,已知卖出的苹果数量与售价之间的关系如图所示,成本为5元/千克,现以8元/千克卖出,赚元.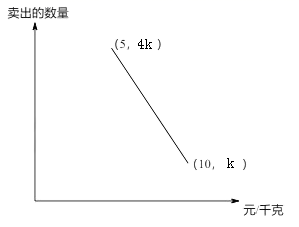 12. 如图,矩形ABCD中,已知:AB=3,AD=5,点P是BC上一点,且△PAD是等腰三角形,则BP= .
12. 如图,矩形ABCD中,已知:AB=3,AD=5,点P是BC上一点,且△PAD是等腰三角形,则BP= .
三、解答题
-
13. 计算:(1)、(2)、14. 如图,在平行四边形ABCD中,对角线AC与BD相交于点O,过点O的直线EF与BA、DC的延长线分别交于点E、F,求证:AE=CF.
 15. 已知:某校有一块四边形空地 , 如图现计划在该空地上种草皮,经测量 , , 若每平方米草皮需元,问需投入多少元?
15. 已知:某校有一块四边形空地 , 如图现计划在该空地上种草皮,经测量 , , 若每平方米草皮需元,问需投入多少元? 16. 如图,在正方形ABCD中,点M是BC边上任意一点,请你仅用无刻度直尺,分别在图1、图2中按要求作图(保留作图痕迹,不这写作法)
16. 如图,在正方形ABCD中,点M是BC边上任意一点,请你仅用无刻度直尺,分别在图1、图2中按要求作图(保留作图痕迹,不这写作法)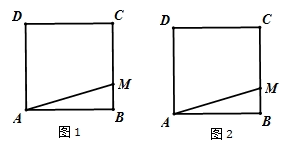 (1)、在图1中,在AB边上求作一点N,连接CN,使得CN=AM;(2)、在图2 中,在AD边上求作一点Q,连接CQ,使得CQ=AM.17. 如图,直线l是一次函数的图象.
(1)、在图1中,在AB边上求作一点N,连接CN,使得CN=AM;(2)、在图2 中,在AD边上求作一点Q,连接CQ,使得CQ=AM.17. 如图,直线l是一次函数的图象.
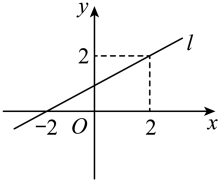 (1)、求出这个一次函数的解析式.(2)、根据函数图象,直接写出时x的取值范围.18. “惜餐为荣,殄物为耻”,为了解落实“光盘行动”的情况,某校数学兴趣小组的同学调研了七、八年级部分班级某一天的餐厨垃圾质量.从七、八年级中各随机抽取10个班的餐厨垃圾质量的数据(单位:kg),进行整理和分析(餐厨垃圾质量用x表示,共分为四个等级:A. , B. , C. , D. ),下面给出了部分信息.
(1)、求出这个一次函数的解析式.(2)、根据函数图象,直接写出时x的取值范围.18. “惜餐为荣,殄物为耻”,为了解落实“光盘行动”的情况,某校数学兴趣小组的同学调研了七、八年级部分班级某一天的餐厨垃圾质量.从七、八年级中各随机抽取10个班的餐厨垃圾质量的数据(单位:kg),进行整理和分析(餐厨垃圾质量用x表示,共分为四个等级:A. , B. , C. , D. ),下面给出了部分信息.七年级10个班的餐厨垃圾质量:0.8,0.8,0.8,0.9,1.1,1.1,1.6,1.7,1.9,2.3.
八年级10个班的餐厨垃圾质量中B等级包含的所有数据为:1.0,1.0,1.0,1.0,1.2.
七八年级抽取的班级餐厨垃圾质量统计表
年级
平均数
中位数
众数
方差
A等级所占百分比
七年级
1.3
1.1
a
0.26
40%
八年级
1.3
b
1.0
0.23
m%
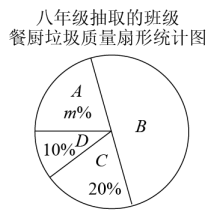
根据以上信息,解答下列问题:
(1)、直接写出上述表中a,b,m的值;(2)、该校八年级共30个班,估计八年级这一天餐厨垃圾质量符合A等级的班级数;(3)、根据以上数据,你认为该校七、八年级的“光盘行动”,哪个年级落实得更好?请说明理由(写出一条理由即可).19. 如图,点C是 的中点,四边形 是平行四边形.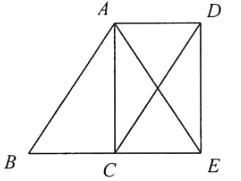 (1)、求证:四边形 是平行四边形;(2)、如果 ,求证:四边形 是矩形.20. 如图,函数 与 的图象交于 .
(1)、求证:四边形 是平行四边形;(2)、如果 ,求证:四边形 是矩形.20. 如图,函数 与 的图象交于 . (1)、求出m,n的值.(2)、直接写出不等式 的解集;(3)、求出 的面积21. 甲、乙两家体育用品商店出售相同的乒乓球和乒乓球拍,乒乓球每盒定价5元,乒乓球拍每副定价40元.现两家商店都搞促销活动,甲店每买一副球拍赠两盒乒乓球;乙店按九折优惠.某班级需购球拍4副,乒乓球x盒.(x≥8)(1)、若在甲店购买付款y甲(元),在乙店购买付款y乙(元),分别写出y与x的函数关系式;(2)、试讨论在哪家商店购买合算?22. 在一次函数学习中,我们经历了“确定函数的表达式——利用函数图象研究其性质——运用函数解决问题的学习过程.在画函数图象时,我们通过描点或平移的方法画出了所学的函数图象.以下是我们研究函数性质及其应用的部分过程,请按要求完成下列各小题.(1)、根据下表信息,求这个函数的解析式,并求出m、n的值;
(1)、求出m,n的值.(2)、直接写出不等式 的解集;(3)、求出 的面积21. 甲、乙两家体育用品商店出售相同的乒乓球和乒乓球拍,乒乓球每盒定价5元,乒乓球拍每副定价40元.现两家商店都搞促销活动,甲店每买一副球拍赠两盒乒乓球;乙店按九折优惠.某班级需购球拍4副,乒乓球x盒.(x≥8)(1)、若在甲店购买付款y甲(元),在乙店购买付款y乙(元),分别写出y与x的函数关系式;(2)、试讨论在哪家商店购买合算?22. 在一次函数学习中,我们经历了“确定函数的表达式——利用函数图象研究其性质——运用函数解决问题的学习过程.在画函数图象时,我们通过描点或平移的方法画出了所学的函数图象.以下是我们研究函数性质及其应用的部分过程,请按要求完成下列各小题.(1)、根据下表信息,求这个函数的解析式,并求出m、n的值;x
…
-4
-3
-2
-1
0
1
2
3
4
…
Y
…
-6
-4
m
0
2
n
-2
-4
-6
…
(2)、在给定的平面直角坐标系中画出该函数图象,判断下列关于该函数性质的说法是否符合题意,正确的在答题卡上相应的括号内打“√”,错误的在答题卡上相应的括号内打“×”;
①该函数图象是轴对称图形,它的对称轴为y轴.( )
②当时,y随x的增大而减小;当时,y随x的增大而增大.( )
(3)、请在同一平面直角坐标系中再画出函数的图象,结合你所画的函数的图象,直接写出不等式的解集.23. 问题解决:如图1,在矩形 中,点 分别在 边上, 于点 .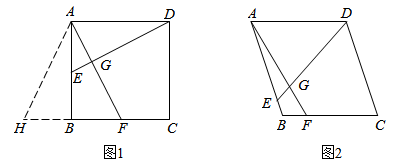 (1)、求证:四边形 是正方形;(2)、延长 到点 ,使得 ,判断 的形状,并说明理由.
(1)、求证:四边形 是正方形;(2)、延长 到点 ,使得 ,判断 的形状,并说明理由.类比迁移:如图2,在菱形 中,点 分别在 边上, 与 相交于点 , ,求 的长.