吉林省四平市铁东区2021-2022学年八年级下学期期末数学试题

试卷更新日期：2022-09-02 类型：期末考试

进入出卷网下载

一、单选题

1. 已知n是正整数， $\sqrt{3 n}$ 是整数，则n的最小值是（）

A、0 B、1 C、3 D、－3

查看试题解析
2. 如图，菱形ABCD的对角线AC、BD相交于点O，BD＝6，AC＝8，E是CD的中点，则OE的长是（）

A、2.5 B、3 C、4 D、5

查看试题解析
3. 下面四个直角坐标系中的直线或曲线，不能表示y是x的函数的是（）

A、 B、 C、 D、

查看试题解析
4. 在同一平面直角坐标系中，函数y＝kx与 $y = \frac{1}{2} x - k$ 的图像大致是（）

A、 B、 C、 D、

查看试题解析
5. 有甲、乙两组数据，如下表所示：
甲
11
12
13
14
15
乙
12
12
13
14
14
两组数据的方差分别是 $s_{甲}^{2}$ 、 $s_{乙}^{2}$ ，则 $s_{甲}^{2}$ 与 $s_{乙}^{2}$ 的大小关系为（）

A、 $s_{甲}^{2} < s_{乙}^{2}$ B、 $s_{甲}^{2} > s_{乙}^{2}$ C、 $s_{甲}^{2} \leq s_{乙}^{2}$ D、 $s_{甲}^{2} \geq s_{乙}^{2}$

查看试题解析
6. 12位参加歌唱比赛的同学的成绩各不相同，按成绩取前6位进入决赛．如果小尹知道了自己的成绩后，要判断自己能否进入决赛，他还要知道这12位同学成绩的（）

A、平均数 B、众数 C、方差 D、中位数

查看试题解析

二、填空题

7. 若式子 $\sqrt{5 x}$ 在实数范围内有意义，则x的取值范围是.

查看试题解析
8. 如图，在△ABC中，D、E、F分别是AB、BC、CA的中点．若△ABC的面积为3，则 $△ D E F$ 的面积为．

查看试题解析
9. 一个木匠要制作矩形的踏板．他在一个对边平行的长木板上分别沿与长边垂直的方向锯两次，就能得到矩形踏板．理由是．

查看试题解析
10. 如图，甲、乙两艘客轮同时离开港口，航行的速度都是40m/min，甲客轮用15min到达点A，乙客轮用20min到达点B．若A，B两点的直线距离为1000m，甲客轮沿着北偏东30°的方向航行，则乙客轮的航行方向是．

查看试题解析
11. 函数 $y = {\begin{array}{l} 3 - x (0 \leq x \leq 2) \\ x - 1 (2 \leq x \leq 4) \end{array}$ 的图像如图所示，则这个函数的最小值是．

查看试题解析
12. 在校园歌手大奖赛上，比赛规则是：七位评委打分，去掉一个最高分和一个最低分后，所剩数据取平均数即为选手的最后得分．七位评委给某位歌手打出的分数如下：9.5，9.4，9.6，9.9，9.3，9.7，9.0，则这位歌手的最后得分是．

查看试题解析
13. 若函数y＝2x＋3与y＝3x－2b的图象交x轴于同一点，则b的值为．

查看试题解析
14. 如图，已知直线 $y = k_{1} x + b_{1}$ 和直线 $y = k_{2} x + b_{2} (k_{1} > 0 ， k_{2} > 0 ， b_{1} < b_{2} ）$ 的交点坐标是（m，n），则关于x的不等式 $k_{1} x + b_{1} < k_{2} x + b_{2}$ 的解集是．

查看试题解析

三、解答题

15. 计算： $(\sqrt{8} - \sqrt{18}) \times \sqrt{6} \div 2 \sqrt{2}$

查看试题解析
16. 如图，在 $▱$ ABCD中，点E，F分别在BC，AD上，且BE=FD，求证：四边形AECF是平行四边形．

查看试题解析
17.

(1)、在直角坐标系中画出直线 $L_{1} ： y = x - 1$ ；

(2)、将直线 $L_{1}$ 向上平移1个单位得到直线 $L_{2}$ ，请直接写出直线 $L_{2}$ 的函数解析式为．

查看试题解析
18. 如图，四边形ABCO是平行四边形，A、B两点的坐标分别为（6，0），（2，4）．

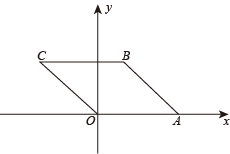(1)、点C的坐标为；

(2)、求直线OC的函数解析式．

查看试题解析
19. 如图， $▱ A B C D$ 的对角线相较于点O，△OAB是等边三角形，AB＝4．

(1)、求证： $▱ A B C D$ 是矩形；

(2)、求AD的长．

查看试题解析
20. 如图，在△ABC中，∠BAC＝90°，AD是BC边上的中线，点E是AD的中点，过点A作 $A F ∥ B C$ ，交BE的延长线于点F，连接CF．

(1)、求证：四边形ADCF是菱形；

(2)、若AB＝AC，试判定四边形ADCF的形状．

查看试题解析
21. 如图，已知过点 $B (1 ， 0)$ 的直线 $l_{1}$ 与直线 $l_{2}$ ： $y = 2 x + 4$ 相交于点 $P (- 1 ， a)$ .

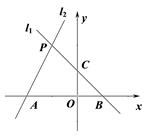(1)、求直线 $l_{1}$ 的解析式；

(2)、求四边形 $P A O C$ 的面积.

查看试题解析
22. 某实验中学八年级甲、乙两班分别选5名同学参加“学雷锋读书活动”演讲比赛，其预赛成绩如图所示：

(1)、根据上图填写下表：

平均数
众数
中位数
方差
甲班
8.5
8.5
0.7
乙班
8.5
8
1.6

(2)、请你分别从平均数、众数、中位数和方差四个方面评价甲、乙两班的预赛成绩，并说明你的理由；

(3)、乙班小明说：“我的成绩是中等水平”，你知道他是几号选手？

查看试题解析
23. 甲、乙两人在一条笔直的道路上相向而行，甲骑自行车从A地到B地，乙驾车从B地到A地，他们分别以不同的速度匀速行驶．已知甲先出发6分钟后，乙再出发，在整个过程中，甲、乙两人的距离y（千米）与甲出发的时间x（分）之间的关系如图所示．

(1)、A、B两地的距离是千米，乙的速度是千米/分；

(2)、乙到达终点后，甲还需分钟到达终点B地；

(3)、求整个过程中y与x的函数解析式，并指出自变量x的取值范围．

查看试题解析
24. 某家具商场计划购进某种餐桌、餐椅进行销售，有关信息如下表：

原进价（元/张）
零售价（元/张）
成套售价（元/套）
餐桌
a
270
500
餐椅
a－110
70
已知用600元购进的餐桌数量与用160元购进的餐椅数量相同．

(1)、上表中a的值为；

(2)、若该商场购进餐椅的数量是餐桌数量的5倍还多20张，且餐桌和餐椅的总数量不超过200张．该商场计划将一半的餐桌成套（一张餐桌和四张餐椅配成一套）销售，其余餐桌、餐椅以零售方式销售．请问怎样进货，才能获得最大利润？最大利润是多少？

查看试题解析
25. 如图，在平面直角坐标系中，直线y＝－x＋8分别交两坐标轴于点A、B，直线CD与直线AB交于点C，与x轴交于点D．点C的横坐标为4，点D在线段OA上，且AD＝7．

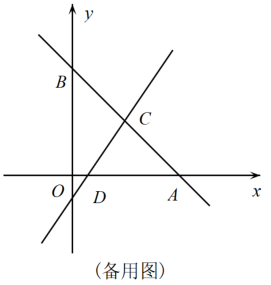
(1)、C、D两点的坐标分别为；

(2)、求直线CD的函数解析式；

(3)、在坐标平面内是否存在这样的点F，使以A、C、D、F为顶点的四边形为平行四边形？若存在，请求出点F的坐标；若不存在，请说明理由．

查看试题解析
26. 如图，在矩形ABCD中，AB＝4，AD＝3，连接BD．点P从点A出发，沿折线AB－BD－DC以每秒1个单位长度的速度向终点C运动．以AP为对角线作正方形AEPF（点F在直线AP的右侧）．设正方形AEPF的面积为S（平方单位），点P的运动时间为t（秒）．

(1)、当点P在线段AB上时，求出S与t之间的函数关系式，并写出t的取值范围；

(2)、当点P在线段DC上时，求出S与t之间的函数关系式，并写出t的取值范围；

(3)、当直线BF将正方形AEPF分成的两部分图形面积相等时，求出t的值．

查看试题解析

	原进价（元/张）	零售价（元/张）	成套售价（元/套）
餐桌	a	270	500
餐椅	a－110	70	500

甲	11	12	13	14	15
乙	12	12	13	14	14

	平均数	众数	中位数	方差
甲班	8.5	8.5		0.7
乙班	8.5		8	1.6