黑龙江省佳木斯市同江市2021-2022学年八年级下学期期末数学试题
试卷更新日期:2022-09-02 类型:期末考试
一、单选题
-
1. 下列各式中计算正确的是( )A、 B、 C、 D、2. 下列曲线中,不表示是的函数图象的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列各组数是勾股数的是( )A、5,12,14 B、6,8,12 C、4,5,6 D、7,24,254. 在一次“爱心互助”捐款活动中,某班第一小组8名同学捐款的金额(单位:元)如下表:
3. 下列各组数是勾股数的是( )A、5,12,14 B、6,8,12 C、4,5,6 D、7,24,254. 在一次“爱心互助”捐款活动中,某班第一小组8名同学捐款的金额(单位:元)如下表:金额/元
10
12
14
20
人数
2
3
2
1
这8名同学捐款的平均金额为( )
A、15元 B、14元 C、13.5元 D、13元5. 如图在▱ABCD中,已知AC=4cm,若△ACD的周长为13cm,则▱ABCD的周长为( )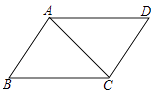 A、26cm B、24cm C、20cm D、18cm6. 小明从家出发步行至学校,停留一段时间后乘车返回,则下列函数图象最能体现他离家的距离(s)与出发时间(t)之间的对应关系的是( )A、
A、26cm B、24cm C、20cm D、18cm6. 小明从家出发步行至学校,停留一段时间后乘车返回,则下列函数图象最能体现他离家的距离(s)与出发时间(t)之间的对应关系的是( )A、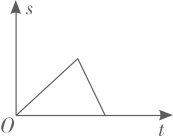 B、
B、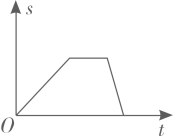 C、
C、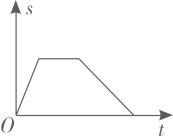 D、
D、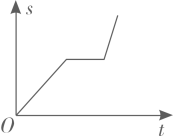 7. 如图所示,是矩形的对角线的中点,为的中点.若 , , 则的周长为( )
7. 如图所示,是矩形的对角线的中点,为的中点.若 , , 则的周长为( )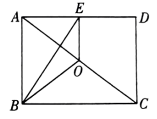 A、10 B、 C、 D、148. 若点 , , 在一次函数(是常数)的图象上,则 , , 的大小关系是( )A、 B、 C、 D、9. 如图,正方形的边长为1, , 是对角线,将绕点顺时针旋转45°得到 , 交于点 , 连接交于点 , 连接 , 则下列结论:①四边形是菱形;②;③;④ . 其中结论正确的是( )
A、10 B、 C、 D、148. 若点 , , 在一次函数(是常数)的图象上,则 , , 的大小关系是( )A、 B、 C、 D、9. 如图,正方形的边长为1, , 是对角线,将绕点顺时针旋转45°得到 , 交于点 , 连接交于点 , 连接 , 则下列结论:①四边形是菱形;②;③;④ . 其中结论正确的是( )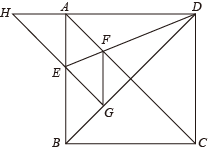 A、①②③ B、①②④ C、②③④ D、①③④
A、①②③ B、①②④ C、②③④ D、①③④二、填空题
-
10. 如果式子有意义,那么x的取值范围是 .11. 若直角三角形的两边长分别为3,4,则该直角三角形的斜边长为 .12. 如图,已知四边形是平行四边形,对角线 , 相交于点 , 添加一个条件 , 使平行四边形是矩形(填一个即可).
 13. “最美鄂州,从我做起”.“五四”青年节当天,马桥村青年志愿小组到胡林社区参加美化社区活动.6名志愿者参加劳动的时间(单位:小时)分别为:3,2,2,3,1,2,这组数据的中位数是.14. 如图,在菱形中,是上一点,连接交对角线于点 , 连接 , 若 , 则°.
13. “最美鄂州,从我做起”.“五四”青年节当天,马桥村青年志愿小组到胡林社区参加美化社区活动.6名志愿者参加劳动的时间(单位:小时)分别为:3,2,2,3,1,2,这组数据的中位数是.14. 如图,在菱形中,是上一点,连接交对角线于点 , 连接 , 若 , 则°. 15. 如图,在中, , 点在上,且 , 以 , 为邻边作平行四边形 , 若 , , 则四边形的面积为 .
15. 如图,在中, , 点在上,且 , 以 , 为邻边作平行四边形 , 若 , , 则四边形的面积为 . 16. 将直线向左平移1个单位长度后,经过点 , 则a的值为 .17. 如图,菱形中,对角线 , , , 分别是 , 的中点,是线段上的一个动点,则的最小值是 .
16. 将直线向左平移1个单位长度后,经过点 , 则a的值为 .17. 如图,菱形中,对角线 , , , 分别是 , 的中点,是线段上的一个动点,则的最小值是 .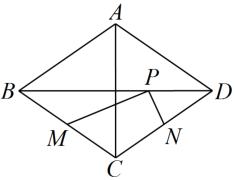 18. 已知正方形ABCD的边长为6,如果P是正方形内一点,且 , 那么AP的长为 .19. 如图,是边长为1的等边三角形,取边中点 , 作 , , , 分别交 , 于点 , , 得到四边形 , 它的面积记作;取中点 , 作 , , , 分别交 , 于点 , , 得到四边形 , 它的面积记作……照此规律作下去,则 .
18. 已知正方形ABCD的边长为6,如果P是正方形内一点,且 , 那么AP的长为 .19. 如图,是边长为1的等边三角形,取边中点 , 作 , , , 分别交 , 于点 , , 得到四边形 , 它的面积记作;取中点 , 作 , , , 分别交 , 于点 , , 得到四边形 , 它的面积记作……照此规律作下去,则 .
三、解答题
-
20. 先化简,再求值: , 其中 .21. 如图,在中,已知 , , 平分 , 于点 , 为中点.求的长.
 22. 如图,已知直线与x轴交于点A,直线与x轴交于点B,且这两条直线交于点C.
22. 如图,已知直线与x轴交于点A,直线与x轴交于点B,且这两条直线交于点C.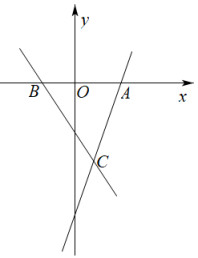 (1)、点A的坐标为 , 点B的坐标为;(2)、这两条直线交点C的坐标为;(3)、求出的面积.23. 某校为了解初中生每天在校体育活动的时间(单位:),随机调查了该校的部分初中生,据随机调查结果,绘制出的统计图①和图②如图.请根据相关信息,解答下列问题:
(1)、点A的坐标为 , 点B的坐标为;(2)、这两条直线交点C的坐标为;(3)、求出的面积.23. 某校为了解初中生每天在校体育活动的时间(单位:),随机调查了该校的部分初中生,据随机调查结果,绘制出的统计图①和图②如图.请根据相关信息,解答下列问题: (1)、本次接受调查的初中生有名,图①中的值为;(2)、直接写出统计的这组每天在校体育活动时间数据的平均数、众数和中位数;(3)、若该校共有800名初中生,估计该校每天在校体育活动时间大于的有多少名.24. 快、慢两车分别从相距的佳市、哈市两地出发,匀速行驶,先相向而行,慢车在快车出发后出发,到达佳市后停止行驶;快车到达哈市后,立即按原路原速返回佳市(快车掉头的时间忽略不计).快、慢两车距哈市的路程(单位:),(单位:)与快车出发时间(单位:)之间的函数图象如图所示,请结合图象信息解答下列问题:
(1)、本次接受调查的初中生有名,图①中的值为;(2)、直接写出统计的这组每天在校体育活动时间数据的平均数、众数和中位数;(3)、若该校共有800名初中生,估计该校每天在校体育活动时间大于的有多少名.24. 快、慢两车分别从相距的佳市、哈市两地出发,匀速行驶,先相向而行,慢车在快车出发后出发,到达佳市后停止行驶;快车到达哈市后,立即按原路原速返回佳市(快车掉头的时间忽略不计).快、慢两车距哈市的路程(单位:),(单位:)与快车出发时间(单位:)之间的函数图象如图所示,请结合图象信息解答下列问题: (1)、直接写出慢车的行驶速度和a的值;(2)、快车与慢车第一次相遇时,距离佳市的路程是多少千米?(3)、快车出发多少小时两车相距?请直接写出答案.25. 在菱形中, , 是射线上一动点,以为边向右侧作等边三角形 , 点的位置随点位置的变化而变化,连接 .
(1)、直接写出慢车的行驶速度和a的值;(2)、快车与慢车第一次相遇时,距离佳市的路程是多少千米?(3)、快车出发多少小时两车相距?请直接写出答案.25. 在菱形中, , 是射线上一动点,以为边向右侧作等边三角形 , 点的位置随点位置的变化而变化,连接 . (1)、如图①,当点在菱形内部或边上时,求证:;(2)、如图②、图③,请分别写出线段 , , 之间的数量关系,不需证明.26. 某公司有A型产品40件,B型产品60件,分配给下属甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完,两商店销售这两种产品每件的利润(元)如下表:
(1)、如图①,当点在菱形内部或边上时,求证:;(2)、如图②、图③,请分别写出线段 , , 之间的数量关系,不需证明.26. 某公司有A型产品40件,B型产品60件,分配给下属甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完,两商店销售这两种产品每件的利润(元)如下表:A型利润
B型利润
甲店
200
170
乙店
160
150
(1)、设分配给甲店A型产品x件,这家公司卖出这100件产品的总利润为W(元),求W关于x的函数关系式,并求出x的取值范围;(2)、若公司要求总利润不低于17560元,说明有多少种不同分配方案,并将各种方案设计出来27. 如图,平面直角坐标系中,把矩形沿对角线所在的直线折叠,点落在点处,与交于点 . , 的长满足式子 . (1)、求点 , 的坐标;(2)、直接写出点的坐标,并求出直线的函数解析式;(3)、是轴上一点,在坐标平面内是否存在点 , 使以 , , , 为顶点的四边形为菱形?若存在,请直接写出点的坐标;若不存在,请说明理由.
(1)、求点 , 的坐标;(2)、直接写出点的坐标,并求出直线的函数解析式;(3)、是轴上一点,在坐标平面内是否存在点 , 使以 , , , 为顶点的四边形为菱形?若存在,请直接写出点的坐标;若不存在,请说明理由.