黑龙江省鸡西市虎林市2021-2022学年八年级下学期期末数学试题
试卷更新日期:2022-09-02 类型:期末考试
一、单选题
-
1. 下列运算正确的是( )A、 B、 C、 D、2. 下列是我们一生活中常见的安全标识,其中是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 化简二次根式得( )A、 B、 C、 D、4. 如图,在中,BE⊥CD,BF⊥AD,∠EBF=45°,CE=3,DF=1,则AF=( )
3. 化简二次根式得( )A、 B、 C、 D、4. 如图,在中,BE⊥CD,BF⊥AD,∠EBF=45°,CE=3,DF=1,则AF=( ) A、 B、 C、 D、5. 已知直角的两边长分别为3和4,第三边为()A、5 B、 C、5或 D、无法确定6. 如图,动点P在边长为2的等边△ABC的边上.它从点A出发,沿A→C→B→A的方向以每秒1个单位长度的速度运动.如果点P的运动时间为t秒,点P与点C之间的距离记为y,那么y与t之间的函数关系用图像表示大致是( )
A、 B、 C、 D、5. 已知直角的两边长分别为3和4,第三边为()A、5 B、 C、5或 D、无法确定6. 如图,动点P在边长为2的等边△ABC的边上.它从点A出发,沿A→C→B→A的方向以每秒1个单位长度的速度运动.如果点P的运动时间为t秒,点P与点C之间的距离记为y,那么y与t之间的函数关系用图像表示大致是( ) A、
A、 B、
B、 C、
C、 D、
D、 7. 如图,矩形中把矩形沿直线折叠,点落在点处,交于点 . 若 , 则的长为( )
7. 如图,矩形中把矩形沿直线折叠,点落在点处,交于点 . 若 , 则的长为( ) A、4 B、5 C、6 D、78. 如图,菱形中, , 于 , 交对角线于 , 过作于 . 若的周长为 , 则菱形的面积为( )
A、4 B、5 C、6 D、78. 如图,菱形中, , 于 , 交对角线于 , 过作于 . 若的周长为 , 则菱形的面积为( )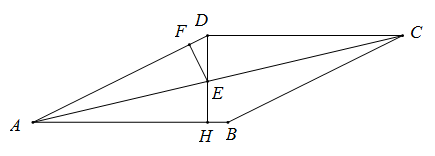 A、 B、 C、 D、9. 甲、乙两人在相同条件下各射击10次,两人的平均环数是8,方差分别是 , , 则成绩较为稳定的是()A、甲 B、乙 C、甲乙一样稳定 D、难以确定10. 如图,四边形ABCD是平行四边形,点E是边CD上一点,且BC=EC,CF⊥BE交AB于点F,P是EB延长线上一点,下列结论:①BE平分∠CBF;②CF平分∠DCB;③BC=FB;④PF=PC.其中正确结论的个数为( )
A、 B、 C、 D、9. 甲、乙两人在相同条件下各射击10次,两人的平均环数是8,方差分别是 , , 则成绩较为稳定的是()A、甲 B、乙 C、甲乙一样稳定 D、难以确定10. 如图,四边形ABCD是平行四边形,点E是边CD上一点,且BC=EC,CF⊥BE交AB于点F,P是EB延长线上一点,下列结论:①BE平分∠CBF;②CF平分∠DCB;③BC=FB;④PF=PC.其中正确结论的个数为( )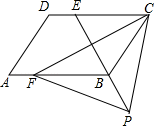 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
11. 如图,已知四边形ABCD,对角线AC和BD相交于O,已知AB∥CD,则添加一个条件可得出四边形ABCD是平行四边形.
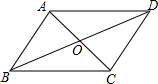 12. 若与最简二次根式是同类二次根式,则 .13. 一组数据4,4,x , 8,8有唯一的众数,则这组数据的平均数是.14. 点和是直线上的两点,且 , 则与的大小关系是 .15. 如图,在平行四边形中,对角线 , 相交于点O,在的延长线上取点E,使 , 连接交于点F,若 , 则 .
12. 若与最简二次根式是同类二次根式,则 .13. 一组数据4,4,x , 8,8有唯一的众数,则这组数据的平均数是.14. 点和是直线上的两点,且 , 则与的大小关系是 .15. 如图,在平行四边形中,对角线 , 相交于点O,在的延长线上取点E,使 , 连接交于点F,若 , 则 . 16. 正比例函数的图象经过二、四象限,那么的取值范围是 .17. 在平行四边形 中, 平分 交边 于 , 平分 交边 于 .若 , ,则 .18. 如图,在Rt△ABC中,∠BAC=90°,且BA=12,AC=16,点D是斜边BC上的一个动点,过点D分别作DE⊥AB于点E , DF⊥AC于点F , 点G为四边形DEAF对角线交点,则线段GF的最小值为 .
16. 正比例函数的图象经过二、四象限,那么的取值范围是 .17. 在平行四边形 中, 平分 交边 于 , 平分 交边 于 .若 , ,则 .18. 如图,在Rt△ABC中,∠BAC=90°,且BA=12,AC=16,点D是斜边BC上的一个动点,过点D分别作DE⊥AB于点E , DF⊥AC于点F , 点G为四边形DEAF对角线交点,则线段GF的最小值为 . 19. 已知:如图,线段AB=6cm,点P是线段AB上的动点,分别以AP、BP为边在AB作等边APC、等边BPD,连接CD,点M是CD的中点,当点P从点A运动到点B时,点M经过的路径的长是cm.
19. 已知:如图,线段AB=6cm,点P是线段AB上的动点,分别以AP、BP为边在AB作等边APC、等边BPD,连接CD,点M是CD的中点,当点P从点A运动到点B时,点M经过的路径的长是cm. 20. 如图,在平面直角坐标系中,函数和的图象分别为直线 , , 过点作轴的垂线交于点 , 过点作轴的垂线交于点 , 过点作轴的垂线交于点 , 过点作轴的垂线交于点 , …依次进行下去,则点的坐标为 .
20. 如图,在平面直角坐标系中,函数和的图象分别为直线 , , 过点作轴的垂线交于点 , 过点作轴的垂线交于点 , 过点作轴的垂线交于点 , 过点作轴的垂线交于点 , …依次进行下去,则点的坐标为 .
三、解答题
-
21. 先化简,再求值: 其中22. 如图,在平面直角坐标系中,已知的三个顶点的坐标分别为 , , .
 (1)、若经过平移后得到 , 已知点的对应点的坐标为 , 画出;(2)、若是关于原点对称的图形,写出各顶点的坐标;(3)、将绕着点按顺时针方向旋转得到 , 画出 .23. 如图,一次函数的图像与正比例函数(为常数,且)的图像都经过 .
(1)、若经过平移后得到 , 已知点的对应点的坐标为 , 画出;(2)、若是关于原点对称的图形,写出各顶点的坐标;(3)、将绕着点按顺时针方向旋转得到 , 画出 .23. 如图,一次函数的图像与正比例函数(为常数,且)的图像都经过 . (1)、求点的坐标及正比例函数的表达式;(2)、利用函数图象比较和的大小并直接写出对应的的取值范围.24. “抗击疫情,无人缺席”,为了打赢这场没有硝烟的战争,做到不聚集,我们所有同学也足不出户在家为抗击疫情而努力.为了了解同学们在家的生活情况,某校对九年级的部分同学做了一次内容为“宅家活动,我在行动”的调查活动,学校将活动方式分为五类,同学们可根据自己的情况必选且只选其中一类,学校收集整理数据后,绘制了如下两幅不完整的统计图,请根据统计图中的信息解答下列问题:
(1)、求点的坐标及正比例函数的表达式;(2)、利用函数图象比较和的大小并直接写出对应的的取值范围.24. “抗击疫情,无人缺席”,为了打赢这场没有硝烟的战争,做到不聚集,我们所有同学也足不出户在家为抗击疫情而努力.为了了解同学们在家的生活情况,某校对九年级的部分同学做了一次内容为“宅家活动,我在行动”的调查活动,学校将活动方式分为五类,同学们可根据自己的情况必选且只选其中一类,学校收集整理数据后,绘制了如下两幅不完整的统计图,请根据统计图中的信息解答下列问题: (1)、这次抽样调查中,一共抽查了名学生;(2)、请补全条形统计图;(3)、请计算扇形统计图中“享受美食”所对应扇形的圆心角的度数;(4)、根据调查结果,估计该校九年级500名学生中采用“听音乐”的减压方式的人数;请谈一下你对在家的同学有哪些建议.25. 快、慢两车分别从相距360千米路程的甲、乙两地同时出发,匀速行驶,先相向而行,快车到达乙地后,停留1小时,然后按原路原速返回,快车比慢车晚1小时到达甲地,快、慢两车距各自出发地的路程y(千米)与出发后所用的时间x(小时)的关系如图所示.
(1)、这次抽样调查中,一共抽查了名学生;(2)、请补全条形统计图;(3)、请计算扇形统计图中“享受美食”所对应扇形的圆心角的度数;(4)、根据调查结果,估计该校九年级500名学生中采用“听音乐”的减压方式的人数;请谈一下你对在家的同学有哪些建议.25. 快、慢两车分别从相距360千米路程的甲、乙两地同时出发,匀速行驶,先相向而行,快车到达乙地后,停留1小时,然后按原路原速返回,快车比慢车晚1小时到达甲地,快、慢两车距各自出发地的路程y(千米)与出发后所用的时间x(小时)的关系如图所示.请结合图象信息解答下列问题:
 (1)、快、慢两车的速度各是多少?(2)、出发多少小时,快、慢两车距各自出发地的路程相等?(3)、直接写出在慢车到达甲地前,快、慢两车相距的路程为150千米的次数.26. 如图,在中, , , D为AB的中点,点E在直线BC上移动,以DE为边向右作等边三角形DEF,连接CF.
(1)、快、慢两车的速度各是多少?(2)、出发多少小时,快、慢两车距各自出发地的路程相等?(3)、直接写出在慢车到达甲地前,快、慢两车相距的路程为150千米的次数.26. 如图,在中, , , D为AB的中点,点E在直线BC上移动,以DE为边向右作等边三角形DEF,连接CF. (1)、当点E在线段BC上移动时,如图①所示,求证:;(2)、当点E在直线BC上移动时,如图②、图③所示,线段EC、CF与AC之间有怎样的数量关系?请直接写出你的猜想.27. 薇菜蕨类植物中紫萁科紫萁类植物是中国目前出口创汇的重要蔬菜之一,具有杀菌消炎,抗病毒,防止脑神经老化等多重功效,珍宝岛地区在扶贫攻坚战中为了推动农民创收,特别研发出保鲜包装和干制两种新产品再将两种产品包装成A,B两种型号的礼盒,每个A型礼盒含2斤干薇菜和2袋鲜薇菜,每个B型礼盒含4斤干薇菜和2袋鲜薇菜.现有1000斤干薇菜和400袋鲜薇菜需要包装销售(包装费用暂时忽略不计)两种礼盒的成本和售价如下表所示(单位:元)
(1)、当点E在线段BC上移动时,如图①所示,求证:;(2)、当点E在直线BC上移动时,如图②、图③所示,线段EC、CF与AC之间有怎样的数量关系?请直接写出你的猜想.27. 薇菜蕨类植物中紫萁科紫萁类植物是中国目前出口创汇的重要蔬菜之一,具有杀菌消炎,抗病毒,防止脑神经老化等多重功效,珍宝岛地区在扶贫攻坚战中为了推动农民创收,特别研发出保鲜包装和干制两种新产品再将两种产品包装成A,B两种型号的礼盒,每个A型礼盒含2斤干薇菜和2袋鲜薇菜,每个B型礼盒含4斤干薇菜和2袋鲜薇菜.现有1000斤干薇菜和400袋鲜薇菜需要包装销售(包装费用暂时忽略不计)两种礼盒的成本和售价如下表所示(单位:元)A型礼盒
B型礼盒
成本
340
410
售价
400
500
根据以上信息,解答下列问题
(1)、将上述干薇菜和鲜薇菜全部包装成A型和B型礼盒,求包装成的两种礼盒的数量各是多少?(2)、若将上述干薇菜和鲜薇菜包装成280个礼盒后全部销售,包装后剩余的干薇菜和鲜薇菜不计入成本和利润,那么怎样包装可获得最大利润?最大利润是多少?(3)、在(2)的条件下,将包装后剩余的干薇菜和鲜薇菜以成本价在当地销售,销售所得用来购买薇菜根苗在养植基地进行无土栽培,若每株薇菜根苗价格为15元,那么可以购买多少株?28. 如图,在平面直角坐标系中,直线交x轴于点A,交y轴于点B,点B的坐标为 . 直线:与直线相交于点C,点C的横坐标为1.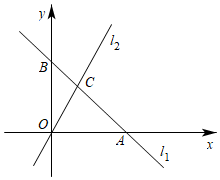 (1)、求直线的解析式;(2)、若点D是y轴上一点,且的面积是面积的 , 求点D的坐标;(3)、平面内是否存在一点E,使得以点O,A,C,E为顶点的四边形是平行四边形?若存在,直接写出符合条件的点E的坐标;若不存在,说明理由.
(1)、求直线的解析式;(2)、若点D是y轴上一点,且的面积是面积的 , 求点D的坐标;(3)、平面内是否存在一点E,使得以点O,A,C,E为顶点的四边形是平行四边形?若存在,直接写出符合条件的点E的坐标;若不存在,说明理由.