河南省濮阳市范县2021-2022学年八年级下学期期末数学试题
试卷更新日期:2022-09-02 类型:期末考试
一、单选题
-
1. 人体中成熟红细胞的平均直径为 , 用科学记数法表示为( )A、 B、 C、 D、2. 下列因式分解正确的是( )A、 B、 C、 D、3. 下列线段a,b,c能组成直角三角形的是( )A、 , , B、 , , C、 , , D、 , ,4. 使分式的值为0,这时x应为( )A、x=±1 B、x=1 C、x=1 且 x≠﹣1 D、x 的值不确定5. 若实数m、n满足 , 且m、n恰好是等腰的两条边的边长,则的周长是( )A、12 B、16 C、12或15 D、156. =成立的条件是( )A、m≥﹣1 B、m≤﹣5 C、﹣1<m≤5 D、﹣1≤m≤57. 矩形具有而一般平行四边形不具有的性质是( )A、两组对边分别相等 B、两组对角分别相等 C、两条对角线互相平分 D、两条对角线相等8. 若x1 , x2 , x3 , ⋯,xn的平均数为8,方差为2,则关于x1+2,x2+2,x3+2,……,xn+2,下列结论正确的是( )A、平均数为8,方差为2 B、平均数为8,方差为4 C、平均数为10,方差为2 D、平均数为10,方差为49. 如图,矩形ABCD中,E,F分别是线段BC,AD的中点,AB=2,AD=4,动点P沿EC,CD,DF的路线由点E运动到点F,则△PAB的面积s是动点P运动的路径总长x的函数,这个函数的大致图象可能是( )
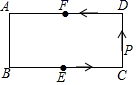 A、
A、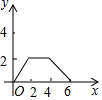 B、
B、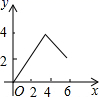 C、
C、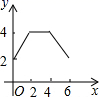 D、
D、 10. 如图,已知正方形的边长为4,点P是对角线上一点,于点E,于点F,连接 . 给出下列结论:
10. 如图,已知正方形的边长为4,点P是对角线上一点,于点E,于点F,连接 . 给出下列结论:①;②四边形的周长为8;
③;④;⑤的最小值为 .
其中正确结论的序号为( )
 A、①②③⑤ B、②③④ C、②③④⑤ D、②③⑤
A、①②③⑤ B、②③④ C、②③④⑤ D、②③⑤二、填空题
-
11. 一个多边形的内角和跟它的外角和相等,则这个多边形是边形.12. 已知点都在直线上,则mn.(填大小关系)13. 某组数据按从小到大的顺序如下:2、4、8、x、10、14,已知这组数据的中位数是9,则这组数据的众数是.14. 计算: .15. 如图,A1B1C1中,A1B1=4,A1C1=5,B1C1=7.点A2 , B2 , C2分别是边B1C1 , A1C1 , A1B1的中点;点A3 , B3 , C3分别是边B2C2 , A2C2 , A2B2的中点;…以此类推,则A2022B2022C2022的周长是 .

三、解答题
-
16. 先化简,再求值: , 其中 .17. 如图,在中,A、C分别在的延长线上,且 .
求证:
 (1)、;(2)、四边形是平行四边形.18. 在我国古代数学著作《九章算术》中记载了一个有趣的问题,这个问题的意思是:
(1)、;(2)、四边形是平行四边形.18. 在我国古代数学著作《九章算术》中记载了一个有趣的问题,这个问题的意思是:如图,有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇沿与一边垂直的方向拉向岸边,它的顶端恰好到达岸边的水面,求池水的深度.
 19. 某校举行了“珍爱生命,预防漏水”主题知识竞赛活动,八(1)、八(2)班各选取五名选手参赛.两班参赛选手成绩依次如下:(单位:分)
19. 某校举行了“珍爱生命,预防漏水”主题知识竞赛活动,八(1)、八(2)班各选取五名选手参赛.两班参赛选手成绩依次如下:(单位:分)八(1)班:8,8,7,8,9
八(2)班:5,9,7,10,9
学校根据两班的成绩绘制了如下不完整的统计图表:
班级
平均数
众数
中位数
方差
八(1)
8
b
c
0.4
八(2)
a
9
9
d
根据以上信息,请解答下面的问题:
(1)、 , , , .(2)、学校根据这些学生的成绩,确定八(1)班为获胜班级,请同学校评定的依据是.
(3)、若八(2)班又有一名学生参赛,考试成绩是8分,则八(2)班这6名选手成绩的平均数与5名选手成绩的平均数相比会.(“变大”“变小”或“不变”)20. 抗击疫情,我们在行动.某药店销售A型和B型两种型号的口罩,销售一箱A型口罩可获利100元,销售一箱B型口罩可获利120元.该药店计划一次购进两种型号的口罩共80箱,其中B型口罩的进货量不超过A型口罩的3倍.设购进A型口罩x箱,这80箱口罩的销售总利润为y元.(1)、求y与x的函数关系式;(2)、该商店购进A型、B型口罩各多少箱,才能使销售利润最大?最大利润是多少?21. 如图,在四边形中, , 对角线交于点O,平分 . (1)、求证:四边形是菱形;(2)、过点D作 , 交的延长线于点E,连接 , 若 , 求菱形的边长.
(1)、求证:四边形是菱形;(2)、过点D作 , 交的延长线于点E,连接 , 若 , 求菱形的边长.


