河北省邢台市威县2021-2022学年八年级下学期期末数学试题

试卷更新日期：2022-09-02 类型：期末考试

进入出卷网下载

一、单选题

1. 一本笔记本5元，买x本共付y元，则变量是（）

A、5 B、5和x C、x D、x和y

查看试题解析
2. 若 $\sqrt{1 - n}$ 是二次根式，则n的值可以是（）

A、 $- 1$ B、2 C、3 D、5

查看试题解析
3. 在平行四边形ABCD中，如果 $∠ A = 35 °$ ，那么 $∠ C$ 的度数是（）

A、 $145 °$ B、 $65 °$ C、 $55 °$ D、 $35 °$

查看试题解析
4. 下列根式是最简二次根式的是（）

A、 $\sqrt{0.5}$ B、 $\sqrt{8}$ C、 $\sqrt{\frac{1}{7}}$ D、 $- \sqrt{3}$

查看试题解析
5. 如图，直线 $A B / / C D$ ， P是直线AB上的动点，当点P的位置变化时，三角形PCD的面积将（）

A、变小 B、变大 C、不变 D、变大变小要看点P向左还是向右移动

查看试题解析
6. 若一次函数y=（k－3）x－1的图象经过第二、三、四象限，则k的取值范围是（）

A、k>0 B、k<0 C、k<3 D、k>3

查看试题解析
7. 在四边形ABCD中， $∠ A = ∠ B = ∠ C = 90 °$ ．如果再添加一个条件可证明四边形是正方形，那么这个条件可以是（）

A、 $A B = B C$ B、 $A B = C D$ C、 $A C = B D$ D、 $∠ D = 90 °$

查看试题解析
8. 甲、乙两人在相同条件下进行射击练习，每人10次射击成绩的平均数都是8环，方差分别是 $S_{甲}^{2} = 0.4 ， S_{乙}^{2} = 1.5$ ，则两人射击成绩波动情况是（）

A、甲波动大 B、乙波动大 C、甲、乙波动一样大 D、无法比较

查看试题解析
9. 下列正确的是（）

A、 $\sqrt{4 + 9} = 2 + 3$ B、 $\sqrt{4 \times 9} = 2 \times 3$ C、 $\sqrt{9^{4}} = \sqrt{3^{2}}$ D、 $\sqrt{4.9} = 0.7$

查看试题解析
10. 课堂上，王老师要求学生设计图形来证明勾股定理，同学们经过讨论，给出两种图形，能证明勾股定理的是（）

A、①行，②不行 B、①不行，②行 C、①，②都行 D、①，②都不行

查看试题解析
11. 已知点 $(- 2 ， m) ， (1 ， n)$ 都在直线 $y = 2 x + b$ 上，则m，n的大小关系是（）

A、 $m > n$ B、m=n C、m＜n D、不能确定

查看试题解析
12. 如图1，在菱形ABCD中，对角线AC、BD相交于O，要在对角线BD上找两点M、N，使得四边形AMCN是菱形，现有图2中的甲、乙两种方案，则正确的方案是（）

A、只有甲 B、只有乙 C、甲和乙 D、甲乙都不是

查看试题解析
13. 有一艘货船从甲港沿直线匀速航行到乙海港，航行途中，发现有一包货物落在水中，便掉头寻找，找到货物后，原地进行打捞，打捞起货物后，按原来的速度到达乙港．若水流的速度忽略不记，设货船出发时间为t，货船离乙港的距离为s，则s与t之的函数关系的大致图象是（）

A、 B、 C、 D、

查看试题解析
14. 五名同学捐款数分别是5，3，6，5，10（单位：元），捐10元的同学后来又追加了10元．追加后的5个数据与之前的5个数据相比，集中趋势相同的是（）

A、只有平均数 B、只有中位数 C、只有众数 D、中位数和众数

查看试题解析

二、填空题

15. 请写出命题“四条边相等的四边形是菱形”的逆命题：，逆命题是一个（填真命题或假命题）．

查看试题解析
16. 已知 $\sqrt{50} - \sqrt{2} = a \sqrt{2} - \sqrt{2} = b \sqrt{2}$ ，则 $a =$ ， $b =$ ．

查看试题解析
17. 在 $5 \times 7$ 正方形网格图中，每个小正方形的边长均为1：

(1)、线段AE是 $△ A B D$ 的；

(2)、点C到AB的距离是．

查看试题解析

三、解答题

18. 计算： $\sqrt{3} (\sqrt{3} - 2 \sqrt{2}) - (\sqrt{3} - \sqrt{2})^{2}$

查看试题解析
19. 如图，在一次地震中，一棵垂直于地面且高度为16米的大树被折断，树的顶部落在离树根8米处，即 $B C = 8$ ，求这棵树在离地面多高处被折断（即求AC的长度）？

查看试题解析
20. 如图，在矩形 $A B C D$ 中，对角线 $A C$ ， $B D$ 相交于点O，若 $∠ B O C = 120 °$ ， $A B = 3$ ，求 $B C$ 的长．

查看试题解析
21. 从甲、乙两个企业随机抽取部分职工，对某个月收入情况进行调查，并把调查结果分别制成扇形统计图和条形统计图．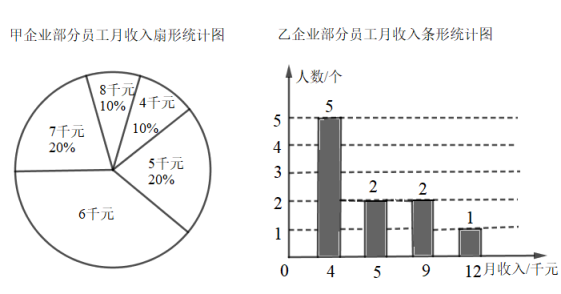

(1)、在扇形统计图中，“6千元”所在的扇形的圆心角是；

(2)、在调查人数中，比较甲企业的平均工资与乙企业的平均工资大小时，小明提出自己的看法：虽然不知道甲企业的调查人数，但是由加权平均数的定义，可以计算甲企业的平均工资，因此可以比较，小明的说法符合题意吗？若符合题意，请比较甲企业的平均工资与乙企业的平均工资大小．

查看试题解析
22. 某零售店销售甲、乙两种蔬菜，甲种蔬菜每千克获利1.1元，乙种蔬菜每千克获利1.5元，该店计划一次购进这两种蔬菜共56千克，并能全部售出．设该店购进甲种蔬菜x千克，销售这56千克蔬菜获得的总利润为y元．

(1)、求y与x的关系式；

(2)、若乙种蔬菜的进货量不超过甲种蔬菜的 $\frac{5}{2}$ ，则该店购进甲、乙两种蔬菜各多少千克时，获得的总利润最大？最大总利润是多少？

查看试题解析
23. 如图，在 $△ A B C$ 中，点D，点E分别是边AC，AB的中点，点F在线段DE上， $∠ A F B = 90 ° ， F G ∥ A B$ 交BC于点G．

(1)、证明：四边形EFGB是菱形；

(2)、若 $A F = 5 ， B F = 12 ， B C = 19$ ，求DF的长度．

查看试题解析
24. 如图，直线 $l_{1} ： y_{1} = \frac{1}{2} x + 2$ 交x轴于点A，交y轴于点B，过点 $C (0 ， 4)$ ，点 $D (2 ， 0)$ 的直线 $l_{2}$ 交直线 $l_{1}$ 于点E．

(1)、求点A与点B坐标；

(2)、求 $S_{△ A D E}$ ；

(3)、现把线段AB沿y轴平移a个单位长度，平移后的线段AB与线段CD组成新图像G，琪琪认为：平移的单位长度 $1 \leq a \leq 3$ 时，图像G的最高点、最低点的纵坐标之差是一个不大于5的固定数值，大家经过反复演算，发现琪琪的说法错误，请通过计算解释琪琪的说法为什么不符合题意．

查看试题解析