河北省唐山市迁安市2021-2022学年八年级下学期期末数学试题
试卷更新日期:2022-09-02 类型:期末考试
一、单选题
-
1. 下列描述物体位置的语句中不能确定物体位置的是( )A、电影院15排10座 B、甲船在乙船北偏东 C、第5节车厢12号座 D、东经 , 北纬2. 下列调查中,适宜采用全面调查(普查)方式的是( )A、了解某市九年级全体学生的体育达标情况 B、某质检部门调查某种罐头厂生产的一批罐头的质量 C、对某厂生产的摩托车头盔进行防撞击性能测试 D、上火车前,对旅客进行安全检查3. 一个圆形花坛,面积S与半径的函数关系式中关于常量和变量的表述正确的是( )A、常量是2,变量是、、 B、常量是2、 , 变量是、 C、常量是2,变量是、 D、常量是 , 变量是、4. 如图,在平面直角坐标系中,☆盖住的点的坐标可能是( )
 A、 B、 C、 D、5. 某鞋店在一周内同一款不同尺码品牌鞋的销量情况如图所示,若尺码不同的每双鞋的利润相同,则下一周该鞋店应多进鞋的尺码是( )
A、 B、 C、 D、5. 某鞋店在一周内同一款不同尺码品牌鞋的销量情况如图所示,若尺码不同的每双鞋的利润相同,则下一周该鞋店应多进鞋的尺码是( ) A、22.5 B、23 C、23.5 D、246. 一个多边形的内角和为 , 外角和为 , 则的多边形的是( )A、
A、22.5 B、23 C、23.5 D、246. 一个多边形的内角和为 , 外角和为 , 则的多边形的是( )A、 B、
B、 C、
C、 D、
D、 7. 一棵树现在的高度为 , 且未来10年内会每年长高 , 设年后树的高度为 , 则与的函数关系式( )A、 B、 C、 D、8. 根据下面的列表,函数表达式正确的是( )
7. 一棵树现在的高度为 , 且未来10年内会每年长高 , 设年后树的高度为 , 则与的函数关系式( )A、 B、 C、 D、8. 根据下面的列表,函数表达式正确的是( )……
0
1
2
……
……
1
3
5
……
A、 B、 C、 D、9. 根据《居民家庭亲子阅读消费调查报告》中的相关数据制成扇形统计图,由图可知,下列说法错误的是( ) A、扇形统计图能反映各部分在总体中所占的百分比 B、每天阅读30分钟以上的居民家庭孩子超过50% C、每天阅读1小时以上的居民家庭孩子占20% D、每天阅读30分钟至1小时的居民家庭孩子对应扇形的圆心角是108°10. 如图(1)是两圆柱形联通容器(联通外体积忽略不计).向甲容器匀速注水,甲容器的水面高度h(cm)随时间t(分)之间的函数关系如图(2)所示,根据提供的图象信息,若甲的底面半径为1cm,则乙容器底面半径为( )
A、扇形统计图能反映各部分在总体中所占的百分比 B、每天阅读30分钟以上的居民家庭孩子超过50% C、每天阅读1小时以上的居民家庭孩子占20% D、每天阅读30分钟至1小时的居民家庭孩子对应扇形的圆心角是108°10. 如图(1)是两圆柱形联通容器(联通外体积忽略不计).向甲容器匀速注水,甲容器的水面高度h(cm)随时间t(分)之间的函数关系如图(2)所示,根据提供的图象信息,若甲的底面半径为1cm,则乙容器底面半径为( ) A、5cm B、4cm C、3cm D、2cm11. 对于命题:一组对边平行且相等的四边形是平行四边形,小明的证明过程( )
A、5cm B、4cm C、3cm D、2cm11. 对于命题:一组对边平行且相等的四边形是平行四边形,小明的证明过程( )已知:如图,在四边形中,且
求证:四边形是平行四边形.
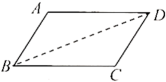
证明:连接 ,
在和中,
∵ , ∴
∵ ,
∴
∴
∴四边形是平行四边形
 A、已经严谨,不用补充 B、应补充“” C、应补充“” D、应补充“”12. 关于一次函数的表述正确的是( )A、若函数图象经过第一、二、四象限,的值可能是3 B、无论为何值,图像一定经过 C、图象与轴的交点坐标 D、若两点 , 在该函数图象上,且 , 则13. 如图,三个边长相同的正方形重叠在一起,、是其中两个正方形的中心,阴影部分的面积和是4,则正方形的边长为( )
A、已经严谨,不用补充 B、应补充“” C、应补充“” D、应补充“”12. 关于一次函数的表述正确的是( )A、若函数图象经过第一、二、四象限,的值可能是3 B、无论为何值,图像一定经过 C、图象与轴的交点坐标 D、若两点 , 在该函数图象上,且 , 则13. 如图,三个边长相同的正方形重叠在一起,、是其中两个正方形的中心,阴影部分的面积和是4,则正方形的边长为( ) A、2 B、4 C、8 D、14. 将40个数据,分为4组,其中第1、2组的频数分别是6、9,第3组的频率是0.3,则第4组的频率是( )A、0.25 B、0.35 C、0.4 D、0.32515. 如图,直线 与 相交于点P,点P的横坐标为 ,则关于x的不等式 的解集在数轴上表示正确的是( )
A、2 B、4 C、8 D、14. 将40个数据,分为4组,其中第1、2组的频数分别是6、9,第3组的频率是0.3,则第4组的频率是( )A、0.25 B、0.35 C、0.4 D、0.32515. 如图,直线 与 相交于点P,点P的横坐标为 ,则关于x的不等式 的解集在数轴上表示正确的是( ) A、
A、 B、
B、 C、
C、 D、
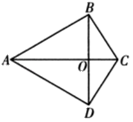
D、 16. 如图,在四边形ABCD中, , , AC,BD交于点O.关于四边形ABCD的形状,甲、乙、丙三人的说法如下:
16. 如图,在四边形ABCD中, , , AC,BD交于点O.关于四边形ABCD的形状,甲、乙、丙三人的说法如下:甲:若添加“”,则四边形ABCD是菱形;
乙:若添加“”,则四边形ABCD是矩形;
丙:若添加“”,则四边形ABCD是正方形.
则说法正确的是( )
 A、甲、乙 B、甲、丙 C、乙、丙 D、甲、乙、丙
A、甲、乙 B、甲、丙 C、乙、丙 D、甲、乙、丙二、填空题
-
17. 函数 中自变量x的取值范围是 .18. 如图,点、分别为的边、的中点,平分 , 交于点 , 连接 , , , 则 , 度.
 19. 如图,动点在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点 , 第2次接着运动到点 , 第3次接着运动到点 , ……按这样的规律第13次运动到点的坐标;经过第2022次运动后,动点的坐标 .
19. 如图,动点在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点 , 第2次接着运动到点 , 第3次接着运动到点 , ……按这样的规律第13次运动到点的坐标;经过第2022次运动后,动点的坐标 .
三、解答题
-
20. 如图,在平面直角坐标系中,的三个顶点坐标分别为 , , .
 (1)、动手操作:画出先向右平移3个单位再向下平移1个单位后的图形;(2)、一只青蛙在线段上,测得位置为 . 请写出按(1)的方式运动后对应位置的坐标:( , );(3)、拓展延伸:把各顶点横、纵坐标都乘以2后,画出放大后的图形;(4)、拓展延伸:直接写出的面积与的面积比 .21. 为响应国家的“双减”政策,某中学对本校初中学生完成家庭作业的时间做了总量控制,规定每天完成家庭作业的时间不超过1.5小时,该校数学课外兴趣小组对本校初中学生回家完成作业的时间做了一次随机抽样调查,并绘制出频数分布表和频数分布直方图(如图)的一部分.
(1)、动手操作:画出先向右平移3个单位再向下平移1个单位后的图形;(2)、一只青蛙在线段上,测得位置为 . 请写出按(1)的方式运动后对应位置的坐标:( , );(3)、拓展延伸:把各顶点横、纵坐标都乘以2后,画出放大后的图形;(4)、拓展延伸:直接写出的面积与的面积比 .21. 为响应国家的“双减”政策,某中学对本校初中学生完成家庭作业的时间做了总量控制,规定每天完成家庭作业的时间不超过1.5小时,该校数学课外兴趣小组对本校初中学生回家完成作业的时间做了一次随机抽样调查,并绘制出频数分布表和频数分布直方图(如图)的一部分.时间(小时)
频数(人数)
频率
4
0.1
0.3
10
6
0.15
合计
1
 (1)、本次抽样调查的样本容量是;(2)、写出在绘制频数分布表和频数分布直方图中的组距是 , 数据总体的大致分布范围是;(3)、在频数分布表中 ▲ ;补全频数分布直方图;(4)、请估计该校1400名初中学生中,约有多少学生在1.5小时以内完成了家庭作业.22. 小明和妈妈决定明天一早爬上1000米高的山顶来欣赏美景.由于临时有事,妈妈没有与小明同时出发.图中的函数图象刻画了小明爬山的路程与出发时间的关系.请解决下列问题:
(1)、本次抽样调查的样本容量是;(2)、写出在绘制频数分布表和频数分布直方图中的组距是 , 数据总体的大致分布范围是;(3)、在频数分布表中 ▲ ;补全频数分布直方图;(4)、请估计该校1400名初中学生中,约有多少学生在1.5小时以内完成了家庭作业.22. 小明和妈妈决定明天一早爬上1000米高的山顶来欣赏美景.由于临时有事,妈妈没有与小明同时出发.图中的函数图象刻画了小明爬山的路程与出发时间的关系.请解决下列问题: (1)、小明在途中休息了分钟;爬到山顶用了分钟;(2)、妈妈坐观光车沿相同路线上山,比小明晚出发40分钟,早10分钟到达山顶,表示妈妈爬山的路程,请在图中画出与的函数图象;(3)、求妈妈与小明相遇时的值.23. 如图,四边形为菱形,已知 , .
(1)、小明在途中休息了分钟;爬到山顶用了分钟;(2)、妈妈坐观光车沿相同路线上山,比小明晚出发40分钟,早10分钟到达山顶,表示妈妈爬山的路程,请在图中画出与的函数图象;(3)、求妈妈与小明相遇时的值.23. 如图,四边形为菱形,已知 , . (1)、直接写出、两点坐标;(2)、求经过、两点的直线解析式;(3)、画出菱形的中心 , 并写出点的坐标;(4)、把(2)的直线沿着轴上下平移 , 若直线与菱形始终有交点,则直接写出的取值范围.24. 某工厂开发生产一种新产品,设生产的产品数量为(件),总销售额为(元),且与之间满足正比例函数关系,当时,;总成本为(元),与之间关系满足表格:
(1)、直接写出、两点坐标;(2)、求经过、两点的直线解析式;(3)、画出菱形的中心 , 并写出点的坐标;(4)、把(2)的直线沿着轴上下平移 , 若直线与菱形始终有交点,则直接写出的取值范围.24. 某工厂开发生产一种新产品,设生产的产品数量为(件),总销售额为(元),且与之间满足正比例函数关系,当时,;总成本为(元),与之间关系满足表格:产品数量(件)
1
2
3
4
总成本(元)
15025
15050
15075
15100
(1)、分别求出、与之间的函数关系式;(2)、设工厂的总利润为(元),求与的函数关系式;(3)、至少生产并销售多少件产品后,工厂才不会亏损.25. 如图,在中, , , 的面积为40,点从出发沿以每秒1个单位长的速度向点匀速运动,到达点时停止运动;点从出发沿以相同速度向点匀速运动,两点同时出发,同时停止,连接、 . 设点、运动的时间是秒 .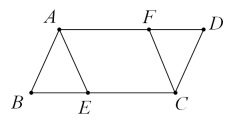 (1)、中边上的高=;(2)、求证:四边形是平行四边形;(3)、当时,是形;(4)、在点、运动的过程中,判断四边形能否成为菱形,如果能,求出的值;如果不能,说明理由.
(1)、中边上的高=;(2)、求证:四边形是平行四边形;(3)、当时,是形;(4)、在点、运动的过程中,判断四边形能否成为菱形,如果能,求出的值;如果不能,说明理由.