河北省唐山市曹妃甸区2021-2022学年八年级下学期期末数学试题
试卷更新日期:2022-09-02 类型:期末考试
一、单选题
-
1. 在平面直角坐标系中,点A(a,2)在第二象限内,则的取值可以是( )A、1 B、-3 C、4 D、4或-42. 下列调查中,不适合采用抽样调查方式的是( )A、调查我区疫情防控期间某封控小区做过4次核酸,2次抗原的人数 B、调查我区居民观看2022年冬奥会开幕式直播的人数 C、调查热播剧《人世间》的收视率 D、调查我区线上学习期间中小学生作业完成情况3. 如图,在菱形ABCD中,E,F分别是AB,AC的中点,如果EF=2,那么菱形ABCD周长是( )
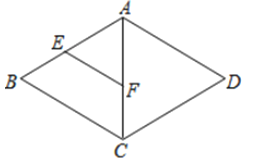 A、4 B、8 C、12 D、164. 函数中自变量的取值范围是( )A、 B、 C、 D、5. 平行四边形相邻两角中,其中一个角的度数与另一个角的度数之间的关系是( )A、 B、 C、 D、6. 下列命题中真命题是( )A、对角线互相垂直的四边形是菱形 B、矩形的四条边相等 C、对角线相等的四边形是矩形 D、菱形的对角线互相垂直7. 点P的坐标是(2-a,3a+6),且点P到两坐标轴的距离相等,则点P坐标是( )A、(3, 3) B、(3,-3) C、(6,-6) D、(3,3)或8. 2022年4月15日是第七个全民国家安全教育日,为了了解某校八年级500名学生对今年国家安全教育日活动主题的知晓情况,从中随机抽取了50名学生进行调查,在这次调查中,样本是( )A、500名学生 B、所抽取的50名学生对国家安全教育日活动主题的知晓情况 C、50名学生 D、每一名学生对国家安全教育日活动主题的知晓情况9. 一次函数的图象经过第一、二、四象限,则m可能的取值为( )A、-1 B、 C、0 D、10. 有三个角是直角的四边形是矩形.
A、4 B、8 C、12 D、164. 函数中自变量的取值范围是( )A、 B、 C、 D、5. 平行四边形相邻两角中,其中一个角的度数与另一个角的度数之间的关系是( )A、 B、 C、 D、6. 下列命题中真命题是( )A、对角线互相垂直的四边形是菱形 B、矩形的四条边相等 C、对角线相等的四边形是矩形 D、菱形的对角线互相垂直7. 点P的坐标是(2-a,3a+6),且点P到两坐标轴的距离相等,则点P坐标是( )A、(3, 3) B、(3,-3) C、(6,-6) D、(3,3)或8. 2022年4月15日是第七个全民国家安全教育日,为了了解某校八年级500名学生对今年国家安全教育日活动主题的知晓情况,从中随机抽取了50名学生进行调查,在这次调查中,样本是( )A、500名学生 B、所抽取的50名学生对国家安全教育日活动主题的知晓情况 C、50名学生 D、每一名学生对国家安全教育日活动主题的知晓情况9. 一次函数的图象经过第一、二、四象限,则m可能的取值为( )A、-1 B、 C、0 D、10. 有三个角是直角的四边形是矩形.已知:如图, .
求证:四边形是矩形.

证明:∵ ,
∴ , ,
∴ , (①),
∵ ,
∴四边形是矩形(②),
在证明过程中,依据①、②分别表示( )
A、①表示同旁内角互补,两直线平行;②表示对角线相等的平行四边形是矩形 B、①表示同旁内角互补,两直线平行;②表示有一个角是直角的平行四边形是矩形 C、①表示两直线平行,同旁内角互补;②表示有一个角是直角的平行四边形是矩形 D、①表示两直线平行,同旁内角互补;②表示对角线相等的平行四边形是矩形11. 如图,在平面直角坐标系中,四边形为正方形,点的坐标为(0,2),点的坐标为(4,0),则点的坐标为( ) A、 B、 C、 D、12. 若顺次连接四边形ABCD各边中点所得四边形是矩形,则四边形ABCD必然是( )A、菱形 B、对角线相互垂直的四边形 C、正方形 D、对角线相等的四边形13. 已知直线与交点的坐标为 , 则方程组的解是( )A、 B、 C、 D、14. 在平面直角坐标系中,将点P (−x,1−x)先向右平移3个单位得点P1 , 再将P1向下平移3个单位得点P2 , 若点P2落在第四象限,则x的取值范围是( )A、 B、 C、 D、或15. 如图表示的是嘉淇父母外出散步时,离家的距离与时间的函数关系.(图代表嘉淇的母亲,图代表嘉淇的父亲)
A、 B、 C、 D、12. 若顺次连接四边形ABCD各边中点所得四边形是矩形,则四边形ABCD必然是( )A、菱形 B、对角线相互垂直的四边形 C、正方形 D、对角线相等的四边形13. 已知直线与交点的坐标为 , 则方程组的解是( )A、 B、 C、 D、14. 在平面直角坐标系中,将点P (−x,1−x)先向右平移3个单位得点P1 , 再将P1向下平移3个单位得点P2 , 若点P2落在第四象限,则x的取值范围是( )A、 B、 C、 D、或15. 如图表示的是嘉淇父母外出散步时,离家的距离与时间的函数关系.(图代表嘉淇的母亲,图代表嘉淇的父亲)①嘉淇的父母出去散步,从家走了20分钟到一个离家900米的报亭;②母亲随即按原来的速度返回;③父亲在报亭看报10分钟;④然后父亲用15分钟返回家.
以上描述,符合函数图象的是( )
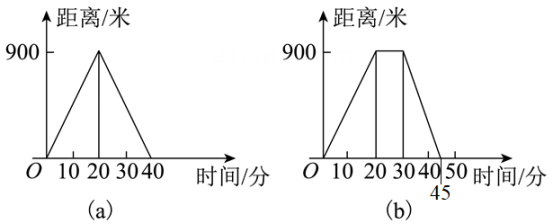 A、①③ B、②④ C、①②③ D、①②③④16. 如图,在一单位为1的方格纸上,△A1A2A3 , △A3A4A5 , △A5A6A7…,都是斜边在x轴上,斜边长分别为2,4,6,…的等腰直角三角形,若A1A2A3的顶点坐标分别为A1(2,0),A2(1,−1),A3(0,0),则依图中所示规律,A2022的坐标为( )
A、①③ B、②④ C、①②③ D、①②③④16. 如图,在一单位为1的方格纸上,△A1A2A3 , △A3A4A5 , △A5A6A7…,都是斜边在x轴上,斜边长分别为2,4,6,…的等腰直角三角形,若A1A2A3的顶点坐标分别为A1(2,0),A2(1,−1),A3(0,0),则依图中所示规律,A2022的坐标为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
17. 为了解我区某一天的气温变化情况,宜用统计图表示;为了解空气中各种气体的占比情况,宜用统计图表示.18. 如图,是嘉淇在体育课上投掷铅球的曲线图,其中表示铅球与投掷点的水平距离,表示铅球在投掷过程中的高度.在铅球出手时,铅球的高度为 , 嘉淇投掷铅球的成绩为 .
 19. 如图,等腰直角三角形的直角边长与正方形的边长均为 , 边与边在同一条直线上,点与点重合,让沿方向运动,当点与点重合时停止运动.运动中两个图形重叠部分的面积与的长度之间的函数关系式为 , 自变量的取值范围是 .
19. 如图,等腰直角三角形的直角边长与正方形的边长均为 , 边与边在同一条直线上,点与点重合,让沿方向运动,当点与点重合时停止运动.运动中两个图形重叠部分的面积与的长度之间的函数关系式为 , 自变量的取值范围是 .
三、解答题
-
20. 如图,在直角坐标系中:
 (1)、描出、、、四点;(2)、顺次连接、、、后得到的图形是;(3)、计算(2)中得到图形的面积.21. 如图,在中,点、在对角线上,且 , 连接、 . 求证: , .
(1)、描出、、、四点;(2)、顺次连接、、、后得到的图形是;(3)、计算(2)中得到图形的面积.21. 如图,在中,点、在对角线上,且 , 连接、 . 求证: , . 22. 某校为了解学生第一个“双减”后的暑假最期待什么活动,校学生会随机对该校八年级部分学生进行了问卷调查,调查结果分为四个类别:表示“广泛阅读”,表示“劳动实践”,表示“户外运动”,表示“其他”.每个同学只能选择其中的一项,根据调查统计结果,绘制成两种不完整的统计图.结合统计图,回答下列问题.
22. 某校为了解学生第一个“双减”后的暑假最期待什么活动,校学生会随机对该校八年级部分学生进行了问卷调查,调查结果分为四个类别:表示“广泛阅读”,表示“劳动实践”,表示“户外运动”,表示“其他”.每个同学只能选择其中的一项,根据调查统计结果,绘制成两种不完整的统计图.结合统计图,回答下列问题. (1)、这次调查的学生总人数为人;(2)、将条形统计图补充完整.扇形统计图中,“户外运动”选项的圆心角为;(3)、该校八年级有800名学生,估计全校八年级学生中最期待“劳动实践”的约有多少名.23. 先阅读下列材料,再解答问题.
(1)、这次调查的学生总人数为人;(2)、将条形统计图补充完整.扇形统计图中,“户外运动”选项的圆心角为;(3)、该校八年级有800名学生,估计全校八年级学生中最期待“劳动实践”的约有多少名.23. 先阅读下列材料,再解答问题.尺规作图:
已知: , D是边上一点,如图1.
求作:四边形 , 使得四边形是平行四边形.
小明的做法如下:

⑴设计方案
先一个正确的草图,如图2,
再分析实现目标的具体方法.

⑵设计作图步骤,完成作图
作法:如图3,
①以点C为圆心、为半径画弧;
②再以点D为圆心、为半径画弧,两弧交于点F;
③连接与 .
∴四边形即为所求.
请在图3中完成尺规作图,保留作图痕迹

⑶推理论证
证明:∵ ,
∴四边形DBCF是平行四边形.( )(填推理依据)
24. 已知商家购进一批产品,成本为10元/件,拟采取线上和线下两种方式进行销售.调查发现,线下的月销售量(单位:件)与线下售价(单位:元/件,)满足一次函数关系,部分数据如下表:(元/件)
13
14
15
16
(件)
1100
1000
900
800
(1)、求与的函数关系式;(2)、当线下售价为多少时,线下月销售量最大,最大是多少件?(3)、若线上售价始终比线下每件便宜2元,且线上的月销售量固定为400件.①求出总利润(单位:元)与线下售价(单位:元/件,)的函数关系式;
②回忆一次函数的概念,请你给上一问求出的函数命名,并用字母表示出它的一般形式.
25. 如图,在平面直角坐标系中,直线经过点和点 , 直线经过原点和点 .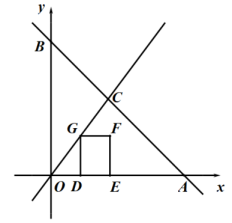 (1)、求直线和直线的表达式;(2)、点是射线上一动点,点关于点的对称点为点 , 过点作轴,交直线于点 . 以、为邻边作矩形 .
(1)、求直线和直线的表达式;(2)、点是射线上一动点,点关于点的对称点为点 , 过点作轴,交直线于点 . 以、为邻边作矩形 .①当点落在直线上时,直接写出长;
②当为等腰三角形时,直接写出点的坐标.(写出一种情况即可)
26. 如图,在矩形中, , , 点从点出发,每秒个单位长度的速度沿方向运动,点从点出发,以每秒2个单位长度的速度沿对角线方向运动.已知点、两点同时出发,当点到达点时,、两点同时停止运动,连接 , 设运动时间为秒. (1)、 , ;(2)、当为何值时,;(3)、在运动过程中,是否存在一个时刻 , 使所得沿它的一边翻折,翻折前后两个三角形组成的四边形为菱形?若存在,求出的值;若不存在,请说明理由.(4)、当点关于点的对称点落在的内部(不包括边上)时,请直接写出的取值范围.
(1)、 , ;(2)、当为何值时,;(3)、在运动过程中,是否存在一个时刻 , 使所得沿它的一边翻折,翻折前后两个三角形组成的四边形为菱形?若存在,求出的值;若不存在,请说明理由.(4)、当点关于点的对称点落在的内部(不包括边上)时,请直接写出的取值范围.