河北省保定市顺平县2021-2022学年八年级下学期期末数学试题

试卷更新日期：2022-09-02 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各式是二次根式的是（）

A、 $\sqrt{- 2}$ B、 $- \sqrt{2}$ C、 $\sqrt[3]{2}$ D、 $\sqrt{x}$

查看试题解析
2. 如图，在平行四边形 $A B C D$ 中，若 $∠ A + ∠ C = 140 °$ ，则 $∠ D$ 的度数为（）

A、 $100 °$ B、 $110 °$ C、 $120 °$ D、 $140 °$

查看试题解析
3. 正比例函数 $y = \frac{1}{3} x$ 的图像大致是（）

A、 B、 C、 D、

查看试题解析
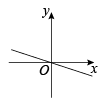4. 下列二次根式中，不是最简二次根式的为（）

A、 $\sqrt{6}$ B、 $\sqrt{7}$ C、 $\sqrt{8}$ D、 $\sqrt{10}$

查看试题解析
5. 直角 $△ A B C$ 的斜边为5，一条直角边为4，则此三角形的面积是（）

A、10 B、20 C、12 D、6

查看试题解析
6. 若 $\sqrt{2}$ 取1.414，则与 $\sqrt{50}$ 最接近的整数是（）

A、6 B、7 C、8 D、10

查看试题解析
7. 平行四边形不一定具有的特征是（）

A、两组对边分别平行 B、两组对角分别相等 C、对角线相等 D、内角和为360°

查看试题解析
8. 下列运算正确的是（）

A、 $\sqrt{5} - \sqrt{3} = \sqrt{2}$ B、 $1 + \sqrt{3} = \sqrt{3}$ C、 $\sqrt{18} \div \sqrt{6} = 3$ D、 $\sqrt{2} \times \sqrt{6} = 2 \sqrt{3}$

查看试题解析
9. 在矩形 $A B C D$ 中， $A B = 6 ， B C = 8$ ，对角线交于点O，则 $B O =$ （）

A、3 B、4 C、5 D、10

查看试题解析
10. 下列曲线中，不能表示y是x的函数的是（）

A、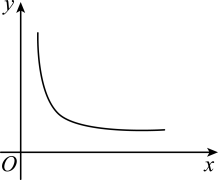 B、 C、 D、

查看试题解析
11. 为落实“五项管理”要求，学校随机抽查了部分学生每天的睡眠时间，统计表如下所示．所抽查学生每天睡眠时间的平均数和中位数分别是（）
睡眠时间/h
6
7
8
9
人数
10
20
15
5

A、7.5，7.5 B、7.5，7 C、7.3，7.5 D、7.3，7

查看试题解析
12. 已知正比例函数 $y = k x$ 的图象经过点 $(- 2 ， 4)$ ，如果 $A (1 ， a)$ 和 $B (- 1 ， b)$ 在该函数的图象上，那么a和b的大小关系是（）

A、 $a \geq b$ B、 $a > b$ C、 $a \leq b$ D、 $a < b$

查看试题解析
13. 在同一平面内，设a、b、c是三条互相平行的直线，已知a与b间的距离为 $5 c m$ ， b与c间的距离为 $2 c m$ ，则a与c间的距离为（）cm．

A、3 B、7 C、3或7 D、2或3

查看试题解析
14. 如图，四边形 $A B C D$ 是平行四边形，下列结论中错误的是（）

A、当 $∠ B A C = 90 °$ 时， $▱ A B C D$ 是菱形 B、当 $∠ A B C = 90 °$ 时， $▱ A B C D$ 是矩形 C、当 $A C ⊥ B D$ 时， $▱ A B C D$ 是菱形 D、当 $A B = B C$ 且 $A C ⊥ B D$ 时， $▱ A B C D$ 是正方形

查看试题解析
15. 如图，在平面直角坐标系中，若菱形 $A B C D$ 的顶点A、B的坐标分别为 $(- 3 ， 0) ， (2 ， 0)$ ，点D在y轴上，则点C的坐标是（）

A、 $(4 ， 4)$ B、 $(4 ， 5)$ C、 $(5 ， 3)$ D、 $(5 ， 4)$

查看试题解析
16. 意大利著名画家达·芬奇用一张纸片剪拼出不一样的空洞，而两个空洞的面积是相等的，如图所示，证明了勾股定理．若设左边图中空白部分的面积为 $S_{1}$ ，右边图中空白部分的面积为 $S_{2}$ ，则下列对 $S_{1} ， S_{2}$ 所列等式错误的是（）

A、 $S_{1} = a^{2} + b^{2} + 2 a b$ B、 $S_{2} = c^{2} + a b$ C、 $S_{1} = S_{2}$ D、 $a^{2} + b^{2} = c^{2}$

查看试题解析

二、填空题

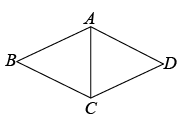
17. 函数 $y = \sqrt{\frac{16}{1 - x}}$ 中，自变量x的取值范围为．当 $x = - 1$ 时，此函数值为．

查看试题解析
18. 如图，在菱形 $A B C D$ 中， $∠ B = 60 °$ ，对角线 $A C = 10$ ，则菱形的周长是，面积是．

查看试题解析
19. 函数 $y = k x + b$ （k，b为常数）的图象如图所示，

(1)、 $k =$ ．

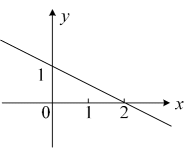(2)、当 $0 < x < 2$ 时，y的取值范围是．

查看试题解析

三、解答题

20. 计算

(1)、 $\sqrt{27} - \sqrt{75} + \sqrt{3}$

(2)、 $2 \sqrt{3} \times \sqrt{8} - \sqrt{12} \times \sqrt{2}$

查看试题解析
21. 如图， $△ A B C$ 中， $A B = A C$ ， $B C$ 长为5，点D是 $A C$ 上的一点， $B D = 4 ， C D = 3$ ．

(1)、 $△ B C D$ 是哪种类型的三角形，请给出证明；

(2)、求出线段 $A C$ 的长．

查看试题解析
22. 2022年5月25、26日国家实施义务教育质量监测．监测部门从某校八年级全体学生中任意抽取40名学生，平均分成甲、乙两个小组参加艺术测试．根据测试成绩绘制出如下的统计表和统计图（成绩均为整数，满分为10分）．
甲组成绩统计表
成绩
7
8
9
10
人数
3
9
3
5
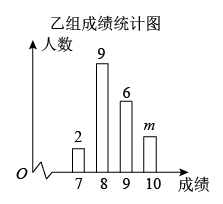
请根据上面的信息，解答下列问题：

(1)、 $m =$ ，甲组成绩的众数是；乙组成绩的中位数是．

(2)、请你计算出甲组的平均成绩．

(3)、已知甲组成绩的方差 $S_{甲}^{2} = 1.05$ ，乙组的平均成绩是8.5，请计算出乙组成绩的方差，并判断哪个小组的成绩更均衡？

查看试题解析
23. 如图，在 $△ A B C $ 中，点D，E，F分别是 $A B ， A C ， B C$ 的中点，连接 $D E ， D F$ ．

(1)、试猜想四边形 $D F C E$ 的形状，并说明理由．

(2)、若 $A C = B C ， ∠ C = 90 °$ ，试判断线段 $C D$ 与 $E F$ 的关系，并说明理由．

查看试题解析
24. 在平面直角坐标系中，一个正比例函数的图象经过点 $(1 ， 2)$ ，把此正比函数的图象向上平移5个单位，得到一次函数： $y = k x + b$ ．

(1)、求一次函数的解析式．

(2)、直线 $y = k x + b (k \neq 0)$ 与x轴交于点A，求A点的坐标．

(3)、点 $B (- 1 ， n)$ 是该直线上一点，点C在x轴上，当 $△ A B C$ 的面积为 $\frac{15}{4}$ 时，请直接写出C点的坐标．

查看试题解析
25. 如图，正方形 $A B C D$ 的周长是40．点P是正方形 $A B C D$ 对角线 $A C$ 上一动点，过P点分别作 $A B$ 、 $B C$ 的垂线，垂足分别为E，F．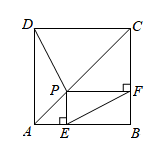

(1)、求证：四边形 $P E B F$ 是矩形．

(2)、请你猜想 $E F$ 与 $D P$ 的数量关系，并给出证明．

(3)、在P点运动过程中， $E F$ 的长也随之变化，求 $E F$ 的最小值．

查看试题解析
26. 在一条笔直的公路上依次有A、C、B三地，A、B两地之间相距 $120 k m$ ，甲车从A地出发到B地停止，乙车从C地出发到B地停止，两车同时出发，甲、乙两车离A地的距离y（单位： $k m$ ）与两车行驶的时间x（单位：h）之间的关系如图所示，

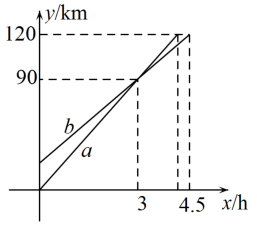(1)、图中线段a表示 ▲ （“甲”或“乙”）车行驶中离A地的距离与时间的关系，求此车到达B地所用的时间．

(2)、求乙车行驶过程中，离A地的距离y与行驶时间x之间的函数关系式．

(3)、求A、C两地之间的距离．

查看试题解析

睡眠时间/h	6	7	8	9
人数	10	20	15	5

成绩	7	8	9	10
人数	3	9	3	5