河北省保定市曲阳县2021-2022学年八年级下学期期末考试数学试题

试卷更新日期：2022-09-02 类型：期末考试

进入出卷网下载

一、单选题

1. 如图，在平行四边形ABCD中，如果∠A＝55°，那么∠B的度数是（）

A、55° B、45° C、125° D、145°

查看试题解析
2. 如图，在△ABC中，D、E分别是AB、AC边上的中点，若DE＝4，则BC等于（）

A、2 B、4 C、8 D、12

查看试题解析
3. 若一个多边形的内角和为 $900 °$ ，则从该多边形的一个顶点出发的对角线条数是（）

A、3 B、4 C、5 D、6

查看试题解析
4. 下列函数：① $y = - 0.1 x$ ；② $y = - 2 x - 1$ ；③ $y = \frac{x}{2}$ ；④ $y = 2 x^{2}$ ；⑤ $y^{2} = 4 x$ .其中，是一次函数的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 一次函数y＝kx－（2－b）的图像如图所示，则k和b的取值范围是（）

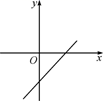A、k>0，b>2 B、k>0，b<2 C、k<0，b>2 D、k<0，b<2

查看试题解析
6. 将一次函数y＝2x－3的图象沿y轴向上平移8个单位长度，所得直线的解析式为（）

A、y＝2x－5 B、y＝2x＋5 C、y＝2x＋8 D、y＝2x－8

查看试题解析
7. 中学生骑电动车上学给交通安全带来隐患，为了解中学2 000名学生家长对“中学生骑电动车上学”的态度，从中随机调查400名家长，结果有360名家长持反对态度，则下列说法正确的是（）

A、调查方式是普查 B、该校只有360名家长持反对态度 C、样本是360名家长 D、该校约有90%的家长持反对态度

查看试题解析
8. 如图，在平面直角坐标系中，等边△OAB的顶点B的坐标为（2，0），点A在第一象限内，将△OAB沿直线OA的方向平移至△O′A′B′的位置，此时点A′的横坐标为3，则点B′的坐标为（）

A、（4，2 $\sqrt{3}$ ） B、（3，3） C、（4，3） D、（3，2）

查看试题解析
9. 某航空公司规定，旅客乘机所携带行李的质量x（kg）与其运费y（元）由如图所示的一次函数图象确定，那么旅客可携带的免费行李的最大质量为（）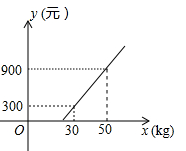

A、20kg B、25kg C、28kg D、30kg

查看试题解析
10. 将图1中两个三角形按图2所示的方式摆放，其中四边形 $A B C D$ 为矩形，连接 $P Q$ ， $M N$ ，甲、乙两人有如下结论：
甲：若四边形 $A B C D$ 为正方形，则四边形 $P Q M N$ 必是正方形；
乙：若四边形 $P Q M N$ 为正方形，则四边形 $A B C D$ 必是正方形．
下列判断正确的是（）

A、甲正确，乙错误 B、甲错误，乙正确 C、甲、乙都错误 D、甲、乙都正确

查看试题解析

二、填空题

11. 某学校初、高六个年级共有2000名学生，为了了解其视力情况，现采用抽样调查，如果按10 %的比例抽样，则样本容量是．

查看试题解析
12. 正比例函数 $y = k x (k \neq 0)$ 的函数值 $y$ 随着 $x$ 增大而减小，则一次函数 $y = x + k$ 的图象大致是（画出草图）．

查看试题解析
13.
如图，正比例函数y=kx，y=mx，y=nx在同一平面直角坐标系中的图象如图所示．则比例系数k，m，n的大小关系是．

查看试题解析
14. 等腰三角形的周长是 $40 c m$ ，腰长 $y (c m)$ 是底边长 $x (c m)$ 的函数．此函数的表达式和自变量取值范围为．

查看试题解析
15. 如图，长方形 $A B C D$ 中， $A B = 3 cm$ ， $A D = 9 cm$ ，将此长方形折叠，使点B与点D重合，折痕为 $E F$ ，则 $△ A B E$ 的面积是．

查看试题解析
16. 已知菱形 $A B C D$ 的周长为 $20 cm$ ，且相邻两内角之比是 $1 ： 2$ ，则菱形的面积是．

查看试题解析
17. 如图，在▱ABCD中，E，F是对角线BD上的两点，要使四边形AFCE是平行四边形，则需添加的一个条件可以是．（只添加一个条件）

查看试题解析
18. 直线 $y = - x + 2$ 和直线 $y = x - 2$ 的交点 $P$ 的坐标是．

查看试题解析
19. 已知在 $△ A B C$ 中， $A C = 6 c m$ ，点D、E分别是AC、BC的中点，连接DE，在DE上有一点F， $E F = 1 c m$ ，连接AF，CF，若 $A F ⊥ C F$ ，则AB＝．

查看试题解析
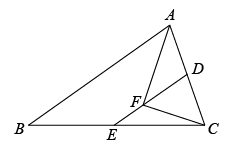20. 如图1，在 $△ A B C$ 中， $A B = A C$ ．动点P从 $△ A B C$ 的顶点A出发，以 $2$ cm／s的速度沿 $A \to B \to C \to A$ 匀速运动回到点A．图2是点P运动过程中，线段 $A P$ 的长度y（cm）随时间t（s）变化的图象．其中点Q为曲线部分的最低点．

(1)、 $A B =$ ；

(2)、图2中，m= ．

查看试题解析

三、解答题

21. 如图，在 $▱ A B C D$ 中， $A E = C F$ ， $M$ 、 $N$ 分别是 $B E$ 、 $D F$ 的中点，试判断四边形 $M F N E$ 的形状，并证明之．

查看试题解析
22. 已知一次函数 $y = (3 m - 7) x + m - 1$ 的图像与 $y$ 轴的交点在 $x$ 轴的上方，且 $y$ 随 $x$ 的增大而减小.

(1)、求整数 $m$ 的值；

(2)、在（1）的结论下，在下面的平面直角坐标系中画出函数的图象，并根据图像回答：当 $x$ 取何值时， $y > 0$ ? $y = 0$ ? $y < 0$ ?

查看试题解析
23. 为了响应市政府创建文明城市的号召，某校调查学生对市“文明公约十二条”的内容了解情况，随机抽取部分学生进行问卷调查，问卷共设置“非常了解”、“比较了解”、“一般了解”、“不了解”四个选项，分别记为A、B、C、D，根据调查结果绘制了如下尚不完整的统计图.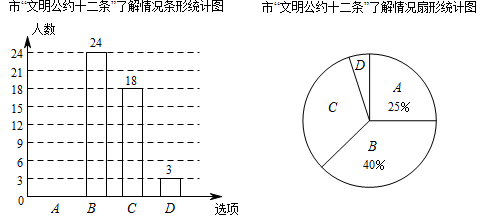

请解答下列问题：

(1)、本次问卷共随机调查了名学生，扇形统计图中C选项对应的圆心角为度；

(2)、请补全条形统计图；

(3)、若该校有1200名学生，试估计该校选择“不了解”的学生有多少人？

查看试题解析
24. 如图，直线 $y_{1} = 2 x - 2$ 与 $y$ 轴交于点 $A$ ，直线 $y_{2} = - 2 x + 6$ 与 $y$ 轴交于点 $B$ ，两条直线交于点 $C$ ．

(1)、求方程组 ${\begin{array}{l} 2 x - y = 2 \\ 2 x + y = 6 \end{array}$ 的解；

(2)、当 $2 x - 2 > 0$ 与 $- 2 x + 6 > 0$ 同时成立时，求 $x$ 的取值范围；

(3)、求 $△ A B C$ 的面积．

查看试题解析
25. 如图，在平面直角坐标系中，已知点 $A (a ， 0)$ ， $B (b ， 0)$ ， $C (2 ， 7)$ ，连接 $A C$ ，交 $y$ 轴于点 $D$ ，且 $a = \sqrt[3]{- 125}$ ， $(\sqrt{b})^{2} = 5$ ．

(1)、求 $△ A O C$ 的面积；

(2)、求点 $D$ 的坐标．

查看试题解析
26. 如图， $A B \begin{array}{l} \begin{array}{l} \begin{array}{l} ∥ \end{array} \end{array} \end{array} C D$ ，点 $E$ ， $F$ 分别在 $A B$ ， $C D$ 上，连接 $E F$ ， $∠ A E F$ 、 $∠ C F E$ 的平分线交于点 $G$ ， $∠ B E F$ 、 $∠ D F E$ 的平分线交于点 $H$ ．

(1)、求证：四边形 $E G F H$ 是矩形；

(2)、过 $G$ 作 $M N \begin{array}{l} \begin{array}{l} \begin{array}{l} ∥ \end{array} \end{array} \end{array} E F$ ，分别交 $A B$ ， $C D$ 于点 $M$ ， $N$ ，过 $H$ 作 $P Q \begin{array}{l} \begin{array}{l} \begin{array}{l} ∥ \end{array} \end{array} \end{array} E F$ ，分别交 $A B$ ， $C D$ 于点 $P$ ， $Q$ ，得到四边形 $M N Q P$ ，此时，求证四边形 $M N Q P$ 是菱形．

查看试题解析