河北省保定市竞秀区2021-2022学年八年级下学期期末数学试题

试卷更新日期：2022-09-01 类型：期末考试

进入出卷网下载

一、单选题

1. 下列四幅作品分别代表“清明”、“谷雨”、“白露”、“大雪”，其中是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 用反证法证明命题“在 $△ A B C$ 中，若 $A B \neq A C$ ，则 $∠ B \neq ∠ C$ ”时，首先应假设（）

A、 $∠ A = ∠ B$ B、 $A B = A C$ C、 $∠ A = ∠ C$ D、 $∠ B = ∠ C$

查看试题解析
3. 如图，将正五边形ABCDE的点C固定，按顺时针方向旋转一定角度，使新五边形的顶点 $D_{1}$ 落在直线BC上，则旋转的最小角度是（）

A、108° B、72° C、54° D、36°

查看试题解析
4. 将分式 $\frac{x^{2}}{2 x + 2 y}$ 中的x，y同时扩大4倍，则分式的值（）

A、扩大4倍 B、扩大2倍 C、缩小到原来的一半 D、保持不变

查看试题解析
5. 若 $x < y$ ，且 $(a - 3) x > (a - 3) y$ ，则a的取值范围是（）

A、 $a < 3$ B、 $a > 3$ C、 $a \geq 3$ D、 $a \leq 3$

查看试题解析
6. 以图（1）（以O为圆心，半径为1的半圆）作为“基本图形”，分别经历如下变换，不能得到图（2）的是（）

A、绕着OB的中点旋转180°即可 B、先绕着点O旋转180°，再向右平移1个单位 C、先以直线AB为对称轴进行翻折，再向右平移1个单位 D、只要向右平移1个单位

查看试题解析
7. 如图， $B F = C E$ ， $A E ⊥ B C$ ， $D F ⊥ B C$ ，添加一个条件____，即可证明 $R t △ A B E$ ≌ $R t △ D C F$ ．下列添加的条件错误的是（）

A、 $A B = D C$ B、 $A E = B F$ C、 $E A = F D$ D、 $∠ A = ∠ D$

查看试题解析
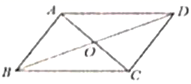
8. 证明：平行四边形对角线互相平分．
已知：四边形ABCD是平行四边形，如图所示．

求证： $A O = C O$ ， $B O = D O$

以下是排乱的证明过程，正确的顺序应是

① $∵ ∠ A B O = ∠ C D O$ ， $∠ B A C = ∠ D C A$ ．② $∵$ 四边形ABCD是平行四边形．③ $∴ A B ∥ C D$ ， $A B = D C$ ．④ $Δ A O B ≅ Δ C O D$ ．⑤ $∴ O A = O C$ ， $O B = O D$ （）

A、②①③④⑤ B、②③⑤①④ C、②③①④⑤ D、③②①④⑤

查看试题解析
9. 若关于x的分式方程 $\frac{m + 4}{x - 3} = 2 - \frac{3 x}{3 - x}$ 有增根，则m的值为（）

A、5 B、4 C、3 D、2

查看试题解析
10. 如图， $A B = C D$ ， $A D = B C$ ， $A D = 4$ ， $B E = 6$ ， $△ D C E$ 的面积为3，则四边形ABCD的面积为（）

A、10 B、12 C、15 D、20

查看试题解析
11. 数学课上，老师让计算 $\frac{2 a}{a - b} + \frac{a - 3 b}{a - b}$ ．佳佳的解答如下：
解：原式 $= \frac{2 a + a - 3 b}{a - b}$ ①
$= \frac{3 a - 3 b}{a - b}$ ②
$= \frac{3 (a - b)}{a - b}$ ③
＝3④
对佳佳的每一步运算，依据错误的是（）

A、①：同分母分式的加减法法则 B、②：合并同类项法则 C、③：逆用乘法分配律 D、④：等式的基本性质

查看试题解析
12. 如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ， AD平分 $∠ C A B$ ，且 $∠ B = 30 °$ ， $A D = 4$ ，点E是AB上一动点，则D，E之间的最小距离为（）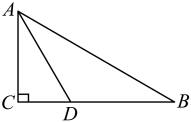

A、8 B、4 C、2 D、1

查看试题解析

13. 如图是李老师在黑板上演示的尺规作图及其步骤，

已知钝角 $Δ A B C$ ，尺规作图及步骤如下：

步骤一：以点 $C$ 为圆心， $C A$ 为半径画弧；

步骤二：以点 $B$ 为圆心， $B A$ 为半径画弧，两弧交于点 $D$ ；

步骤三：连接 $A D$ ，交 $B C$ 延长线于点 $H$ ．

下面是四位同学对其做出的判断：

小明说： $B H ⊥ A D$ ；

小华说： $∠ B A C = ∠ H A C$ ；

小强说： $B C = H C$ ；

小方说： $A H = D H$ ．

则下列说法正确的是（）

A、只有小明说得对 B、小华和小强说的都对 C、小强和小方说的都不对 D、小明和小方说的都对

查看试题解析

14. 若不等式组 ${\begin{array}{l} x - 2 \geq 0 \\ 2 x < m \end{array}$ 无解，则m的值可能（）

A、7 B、6 C、3 D、5

查看试题解析
15. 如图，点E、F分别是▱ABCD边AD、BC的中点，G、H是对角线BD上的两点，且BG=DH．则下列结论中错误的是（）

A、 $G F = E H$ B、四边形EGFH是平行四边形 C、 $E G = F H$ D、 $E H ⊥ B D$

查看试题解析
16. 某飞行器在相距为m的甲、乙两站间往返飞行．在没有风时，飞行器的速度为v，往返所需时间为 $t_{1}$ ；如果风速度为 $p (0 < p < v)$ ，则飞行器顺风飞行速度为 $(v + p)$ ，逆风飞行速度为 $(v - p)$ ，往返所需时间为 $t_{2}$ ．则 $t_{1}$ 、 $t_{2}$ 的大小关系为（）

A、 $t_{1} < t_{2}$ B、 $t_{1} \leq t_{2}$ C、 $t_{1} \geq t_{2}$ D、无法确定

查看试题解析

二、填空题

17. 因式分解： $x^{2} - 4 x =$ ．

查看试题解析
18. 如图，在 $△ A B C$ 中， $A B = 4$ ， $B C = 6$ ， $∠ B = 60 °$ ，将 $△ A B C$ 沿BC所在直线向右平移得到 $△ A^{'} B^{'} C^{'}$ ，连接 $A^{'} C$ ，若 $B B^{'} = 2$ ，则线段 $A^{'} C$ 的长为．

查看试题解析
19. 对于平面直角坐标系xOy中第一象限内的点 $P (x ， y)$ 和图形W，给出如下定义：过点P作x轴和y轴的垂线，垂足分别为M，N，若图形W中的任意一点 $Q (a ， b)$ 满足 $a \leq x$ 且 $b ≤ y$ ，则称四边形PMON是图形W的一个覆盖，点P为这个覆盖的一个特征点．例：若 $M (1 ， 3)$ ， $N (4 ， 3)$ ，则点 $P (5 ， 4)$ 为线段MN的一个覆盖的特征点．已知 $A (1 ， 3)$ ， $B (3 ， 1)$ ， $C (2 ， 3)$ ，请回答下列问题：

(1)、在 $P_{1} (3 ， 3)$ ， $P_{2} (3 ， 2)$ ， $P_{3} (1 ， 2)$ 中，是 $△ A B C$ 的覆盖特征点的是；

(2)、若在一次函数 $y = m x + 5 (m \neq 0)$ 的图象上存在 $△ A B C$ 的覆盖的特征点，则m的取值范围是．

查看试题解析

三、解答题

20. 已知 $4 x - y = 1$ ．

(1)、用含x的代数式表示y为；

(2)、若y的取值范围如图所示，求x的正整数值．

查看试题解析
21. 先化简 $(\frac{1}{x + 2} + 1) \div \frac{x^{2} + 6 x + 9}{x^{2} - 4}$ ，然后再从 $- 3$ ， $- 2$ ， 2，3中选一个合适的数作为x的值代入求值．

查看试题解析
22. 如图，正方形网格中，每个小正方形的边长都是一个单位长度，在平面直角坐标系中， $△ A B C$ 的三个顶点 $A (5 ， 5)$ ， $B (6 ， 3)$ ， $C (2 ， 1)$ 均在格点上．

(1)、画出将 $△ A B C$ 向左平移8个单位长度得到的 $△ A_{1} B_{1} C_{1}$ ；

(2)、 $△ A_{1} B_{1} C_{1}$ 绕点 $C_{1}$ 顺时针旋转90°后得到 $△ A_{2} B_{2} C_{1}$ ，请在图中标出点 $A_{2}$ ，写出点 $A_{2}$ 的坐标为；

(3)、过点 $A_{2}$ 的直线l将四边形 $B B_{1} C_{1} C$ 分成面积相等的两部分，请在图中画出直线l．

查看试题解析
23. 如图，在 $△ A B C$ 中，D、E分别为AB、AC的中点，过点C作 $C F / / B D$ 交DE的延长线于点F．

(1)、求证：四边形BCFD为平行四边形；

(2)、若 $B C = 6$ ，求EF的长．

查看试题解析
24. 教材中写道：“形如 $a^{2} \pm 2 a b + b^{2}$ 的式子称为完全平方式”．如果一个多项式不是完全平方式，我们常做如下变形：先添加一个适当的项，使式子中出现完全平方式，再减去这个项，使整个式子的值不变，这种方法叫做配方法．配方法是一种重要的解决数学问题的方法，不仅可以将有些看似不能分解的多项式分解因式，还能解决一些与非负数有关的问题及求代数式最大、最小值等问题，
例如：分解因式 $x^{2} + 2 x - 3$ ．
原式 $= x^{2} + 2 x + 1 - 1 - 3 = (x^{2} + 2 x + 1) - 4 = {(x + 1)}^{2} - 4 = (x + 1 + 2) (x + 1 - 2)$
$= (x + 3) (x - 1)$ ；
例如：求代数式 $x^{2} + 4 x + 6$ 的最小值．
原式 $= x^{2} + 4 x + 4 - 4 + 6 = x^{2} + 4 x + 4 + 2 = {(x + 2)}^{2} + 2$ ．
∵ ${(x + 2)}^{2} \geq 0$ ， ∴当 $x = - 2$ 时， $x^{2} + 4 x + 6$ 有最小值是2．
解决下列问题：

(1)、若多项式 $x^{2} + 6 x + m$ 是一个完全平方式，那么常数m的值为；

(2)、分解因式： $x^{2} + 6 x - 16 =$ ；

(3)、若 $x > - 1$ ，比较： $x^{2} + 6 x + 5$ （）0（填“＞，＜或＝”），并说明理由；

(4)、求代数式 $- x^{2} - 6 x - 5$ 的最大或最小值．

查看试题解析
25. 某新能源汽车经销商分别花费60万元，32万元购进A，B两种型号的新能源汽车若干辆．已知A型汽车的进货单价比B型汽车的进货单价高4万元，且购进A型汽车的数量是B型汽车的数量的1.5倍．

(1)、求A，B两种型号汽车的进货单价；

(2)、由于新能源汽车需求不断增加，该店准备再次购进A，B两种型号的新能源汽车60辆，已知A型车的售价为25万元/辆，B型车的售价为20万元/辆．根据销售经验，购进B型车的数量不少于A型车的2倍．如果设将这60辆汽车全部售完会获利w万元，那么该经销商应购进A型车多少辆，才能使w最大？w最大为多少万元？

查看试题解析
26. 如图1， $∠ A C D = 90 °$ ， $A C = D C$ ， MN是过点A的直线，过点D作 $D B ⊥ M N$ 于点B，连接CB；过点C作 $C E ⊥ C B$ ，与MN交于点E．

(1)、连接AD，AD是AC的倍；

(2)、直线MN在图1所示位置时，可以得到线段BD和AE的数量关系是 ▲ ， $B D - B A$ 与BC之间的数量关系是 ▲ ，请证明你的结论；

(3)、直线MN绕点A旋转到图2的位置，若 $B D = 2$ ， $B C = \sqrt{2}$ ，则AB的长为（直接写结果）；

(4)、直线MN绕点A旋转到图3的位置时，直接写出线段BA，BC，BD之间的数量关系．

查看试题解析