广东省河源市紫金县2021-2022学年八年级下学期期末数学试题

试卷更新日期：2022-09-01 类型：期末考试

进入出卷网下载

一、单选题

1. 一个关于x的一元一次不等式组的解集在数轴上的表示如图，则该不等式组的解集是（）

A、x＞1 B、x≥1 C、x＞3 D、x≥3

查看试题解析
2. 到△ABC的三边距离相等的点是△ABC的（）

A、三边中线的交点 B、三条角平分线的交点 C、三边上高的交点 D、三边垂直平分线的交点

查看试题解析
3. 以下分别是回收、节水、绿色包装、低碳4个标志，其中是中心对称图形的是（）．

A、 B、 C、 D、

查看试题解析
4. 计算 $(\frac{a}{b} - \frac{b}{a}) \div \frac{a - b}{a}$ 的结果为（）

A、 $\frac{a + b}{b}$ B、 $\frac{a - b}{b}$ C、 $\frac{a - b}{a}$ D、 $\frac{a + b}{a}$

查看试题解析
5. 若分式 $\frac{x}{| x | - 1}$ 无意义，则x的值是（）

A、0 B、1 C、-1 D、 $± 1$

查看试题解析
6. 若一个正多边形的每一个外角都等于36°，则它是（）

A、正九边形 B、正十边形 C、正十一边形 D、正十二边形

查看试题解析
7. 如图，在▱ABCD中，F是AD上的一点，CF＝CD．若∠B＝72°，则∠AFC的度数是（）

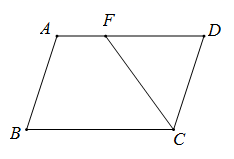A、144° B、108° C、102° D、78°

查看试题解析
8. 下列各式从左到右的变形中，是因式分解的为（）．

A、 $x (a - b) = a x - b x$ B、 $x^{2} - 1 + y^{2} = (x - 1) (x + 1) + y^{2}$ C、 $x^{2} - 1 = (x + 1) (x - 1)$ D、 $a x + b x + c = x (a + b) + c$

查看试题解析
9. 若不等式组 ${\begin{array}{l} x < 8 \\ x > n \end{array}$ 有解，那么 $n$ 的取值范围是（）

A、 $n > 8$ B、 $n \leq 8$ C、 $n < 8$ D、 $n \leq 8$

查看试题解析
10. 下列命题：
①等腰三角形的角平分线、中线和高重合；②等腰三角形两腰上的高相等；③等腰三角形的最短边是底边；④等边三角形的高、中线、角平分线都相等；⑤等腰三角形都是锐角三角形．其中正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 分解因式： $3 a^{2} + 12 a + 12 =$ ．

查看试题解析
12. 已知点M的坐标为（2，1），若将点M关于原点的对称点先向右平移3个单位长度，再向下平移2个单位长度，则所得点的坐标为．

查看试题解析
13.
小菲受《乌鸦喝水》故事的启发，利用量筒和体积相同的小球进行了如下操作，请根据图中给出的信息，量筒中至少放入小球时有水溢出．

查看试题解析
14. 在 $△$ ABC中，∠A＝40°，AB的垂直平分线分别交AB，AC边于点D，E，若AE＝BC，则 $∠ A B C$ ＝．

查看试题解析
15. 在△ABC中，∠C＝90°，BC＝6，AC＝8，顺次连接△ABC各边中点，得到的三角形面积是．

查看试题解析
16. 已知非零实数x，y满足 $y = \frac{x}{x + 1}$ ，则 $\frac{x - y + 3 x y}{x y}$ 的值等于.

查看试题解析
17. 如图，在平行四边形ABCD中，AB＝3，AD＝4，∠ABC＝60°，过BC的中点E作EF⊥AB于点F，交DC的延长线于点G，则DE＝．

查看试题解析

三、解答题

18. 解不等式组： ${\begin{array}{l} 2 x > 3 x - 2 \\ \frac{2 x - 1}{3} \geq \frac{1}{2} x - \frac{2}{3} \end{array}$

查看试题解析
19. 解方程： $\frac{3}{x - 1} - \frac{x + 3}{x^{2} - 1} = 0$ ．

查看试题解析
20. 先化简，再求值： $\frac{x^{2} - y^{2}}{x^{2} - 2 x y + y^{2}}$ ，其中 $x = 110$ ， $y = 10$ ．

查看试题解析
21. 如图，在△ABC和△DCB中，∠A=∠D=90°，AC=BD，AC与BD相交于点O．

(1)、求证：△ABC≌△DCB；

(2)、求证：△OBC是等腰三角形．

查看试题解析
22. 图，△ABC 是边长为 2 的等边三角形，将△ABC 沿直线 BC 平移到△DCE 的位置，连接 BD，

(1)、△ABC 平移的距离为；

(2)、求 BD 的长．

查看试题解析
23. 在四边形 $A B C D$ 中， $A C$ 、 $B D$ 交于点 $O$ ， $A D ∥ B C$ ， $B O = D O$ ．

(1)、证明：四边形 $A B C D$ 是平行四边形；

(2)、过点 $O$ 作 $O E ⊥ B D$ 交 $B C$ 于点 $E$ ，连接 $D E$ ．若 $∠ C D E = ∠ C B D = 15 °$ ，求 $∠ A B C$ 的度数．

查看试题解析
24. 在2019年春季环境整治活动中，某社区计划对面积为 $1600 m^{2}$ 的区域进行绿化.经投标，由甲、乙两个工程队来完成，若甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍，并且在独立完成面积为 $400 m^{2}$ 区域的绿化时，甲队比乙队少用5天.

(1)、求甲、乙两工程队每天能完成绿化的面积；

(2)、设甲工程队施工 $x$ 天，乙工程队施工 $y$ 天，刚好完成绿化任务，求 $y$ 关于 $x$ 的函数关系式；

(3)、在（2）的条件下，若甲队每天绿化费用是0.6万元，乙队每天绿化费用为0.25万元，且甲乙两队施工的总天数不超过25天，则如何安排甲乙两队施工的天数，使施工总费用最低？并求出最低费用.

查看试题解析
25. 在△ABC中，AB=AC，∠A=60°，点D是线段BC的中点，∠EDF=120°，DE与线段AB相交于点E，DF与线段AC（或AC的延长线）相交于点F．

(1)、如图1，若DF⊥AC，垂足为F，AB=4，求BE的长；

(2)、如图2，将（1）中的∠EDF绕点D顺时针旋转一定的角度，DF仍与线段AC相交于点F．求证： $B E + C F = \frac{1}{2} A B$ ；

(3)、如图3，将（2）中的∠EDF继续绕点D顺时针旋转一定的角度，使DF与线段AC的延长线交于点F，作DN⊥AC于点N，若DN=FN，求证： $B E + C F = \sqrt{3} (B E - C F)$ ．

查看试题解析