安徽省芜湖市无为市2021-2022学年八年级下学期期末数学试题

试卷更新日期：2022-09-01 类型：期末考试

进入出卷网下载

一、单选题

1. 要使式子 $\frac{3}{\sqrt{6 - 2 x}}$ 在实数范围内有意义，则x的取值范围是（）

A、 $x < 3$ B、 $x \geq 3$ C、 $x \leq 3$ D、 $x \neq 3$

查看试题解析
2. 已知 $△ A B C$ 的三条边分别为a，b，c，下列条件不能判断 $△ A B C$ 是直角三角形的是（）

A、 $c^{2} = a^{2} - b^{2}$ B、 $∠ A ： ∠ B ： ∠ C = 3 ： 4 ： 5$ C、 $a = 5$ ， $b = 13$ ， $c = 12$ D、 $∠ A = ∠ B + ∠ C$

查看试题解析
3. 下面计算结果正确的是（）

A、 $\sqrt{7} - \sqrt{5} = \sqrt{2}$ B、 $\sqrt{3} + 2 \sqrt{3} = 3 \sqrt{3}$ C、 $2 \sqrt{6} \div 2 \sqrt{3} = 2 \sqrt{2}$ D、 $2 \sqrt{2} \times 3 \sqrt{3} = 6 \sqrt{5}$

查看试题解析
4. 两只蚂蚁在水平地面上从同一地点出发，一只以每分钟12cm的速度朝正东方向爬行，一只以每分钟16cm的速度朝正南方向爬行，10分钟之后两只蚂蚁相距（）

A、120cm B、160cm C、200cm D、280cm

查看试题解析
5. 已知 $P (- 2 ， 4)$ ， $Q (3 ， - 6)$ ， $R$ $(1 ， - 2)$ ， $S (- 2 ， 6)$ 中有三个点在同一直线 $y = k x$ 上，不在此直线上的点是（）

A、点 $P$ B、点 $Q$ C、点 $R$ D、点 $S$

查看试题解析
6. 为了从四名同学中选出一人参加计算机编程比赛，对他们进行了多次测试，并对每个人的测试成绩的平均数及方差进行了统计（如下表），则应选的同学是（）
学生
学生一
学生二
学生三
学生四
平均数
95
96
96
95
方差
5
5
4.8
4.8

A、学生一 B、学生二 C、学生三 D、学生四

查看试题解析
7. 如图，四边形ABCD是平行四边形，以点A为圆心，AB的长为半径画弧，交AD于点F；分别以点B，F为圆心，大于 $\frac{1}{2} B F$ 的长为半径画弧，两弧相交于点G：连接AG并延长，交BC于点E．连接BF，若 $A E = 2 \sqr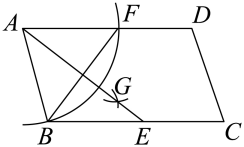t{10}$ ， $B F = 2 \sqrt{6}$ ，则AB的长为（）

A、3 B、4 C、5 D、8

查看试题解析
8. 下列说法正确的是（）

A、对角线互相垂直的四边形是菱形 B、四条边都相等的四边形是正方形 C、一组对边平行，另一组对边相等的四边形是平行四边形 D、四个角相等的四边形是矩形

查看试题解析
9. 据统计，无为市某月4日~10日的最高气温如下发所示，则下列说法错误的是（）

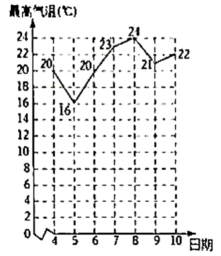A、平均数是20 B、众数是20 C、5日~8日最高气温呈上升趋势 D、中位数是21

查看试题解析
10. 如图，在平面直角坐标系中，点 $A (3 ， a)$ 是直线 $y = 2 x$ 与直线 $y = x + b$ 的交点，点B是直线 $y = x + b$ 与y轴的交点，点P是x轴上的一个动点，连接PA，PB，则 $P A + P B$ 的最小值是（）

A、6 B、 $3 \sqrt{5}$ C、9 D、 $3 \sqrt{10}$

查看试题解析

二、填空题

11. 已知 $x = \sqrt{6 a} \div \sqrt{2 a}$ ，则 ${(x + \sqrt{3})}^{2}$ 的值为．

查看试题解析
12. 直角三角形的两直角边长是 $\sqrt{3} c m$ 和3cm，则它的斜边上的高是cm．

查看试题解析
13. 如图，矩形ABCD的对角线AC与BD交于点O，过点O作 $O E ⊥ A C$ ，交AD于点E，过点E作 $E F ⊥ B D$ ，垂足为F， $E F = 1$ ， $O E = 2$ ， $B D = 4 \sqrt{3}$ ，则矩形ABCD的面积为．

查看试题解析
14. 如图，直线 $y = - \frac{4}{3} x + 4$ 与x轴，y轴分别交于点A，B，将直线 $y = - \frac{4}{3} x + 4$ 向左平移得到一条新的直线，它与x轴，y轴分别交于点C，D．若 $B D - A B = 3$ ，则

(1)、点D的坐标是；

(2)、直线CD的解析式为 $y =$ ．

查看试题解析

三、解答题

15. 计算： $4 \sqrt{\frac{1}{2}} - \sqrt{18} + （ 1 - \sqrt{3} ）^{0} + | \sqrt{2} - 1 |$ ．

查看试题解析
16. 如图，在 $△ A B C$ 中，D，E，F分别是AB，BC，CA的中点， $A C = 20$ ， $B C = 18$ ，求四边形DECF的周长．

查看试题解析
17. 已知 $5 + \sqrt{10}$ 的小数部分是a， $5 - \sqrt{10}$ 的小数部分b，求ab的值．

查看试题解析
18. 如图，一只小鸟旋停在空中A点，A点到地面的高度 $A B = 20$ 米，A点到地面C点（B、C两点处于同一水平面）的距离 $A C = 25$ 米．若小鸟竖直下降12米到达D点（D点在线段AB上），求此时小鸟到地面C点的距离．

查看试题解析
19. 如图，函数 $y = 3 x$ 和 $y = k x + 5$ 的图象相交于点 $A (a ， 3)$ ．

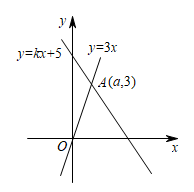(1)、求a，k的值；

(2)、根据图象，直接写出不等式 $3 x < k x + 5$ 的解集．

查看试题解析
20. 如图，正方形ABCD中，E是对角线BD上一点，连接AE，CE，延长AE交CD边于点F．

(1)、求证： $∠ A E B = ∠ C E B$ ．

(2)、若 $∠ A E C = 2 α$ ， $∠ A F D = β$ ，求证： $α + β = 135 °$ ．

查看试题解析
21. 电影《长津湖》和《水门桥》是两部聚焦抗美援朝历史的影片，从观看过这两部电影的学生中各随机抽取了20名学生进行调查，让他们给这两部电影评分，下列图表是调查中的部分信息．
根据以上信息，解答下列问题：

(1)、电影《长津湖》得分的中位数和众数分别是多少？

(2)、电影《水门桥》得分的平均数是多少？

(3)、若该校有200名学生观看过这两部影片，且他们都对这两部作品进行评分，你认为这两部作品一共可以得到多少个满分？

查看试题解析
22. 文具店打算用5000元（全部用完）购进A、B两种类型的计算器进行零售，进价和零售价如下表所示：
类型
进价（元/个）
零售价（元/个）
A型计算器
50
80
B型计算器
25
45
若购进A类型的计算器x个，B类型的计算器y个，请解决下列问题．

(1)、求y与x之间的函数表达式；

(2)、若A、B两种类型的计算器的进货总数不超过150个，请问文具店如何进货，才能使两种计算器全部卖完后能获得最大利润？

查看试题解析
23. 如图，在矩形ABCD中， $A B = 12$ ， $A D = 16$ ， E，F分别是AD，BC的中点，G、H是对角线AC上的两个动点，且分别从点A、点C同时都以每秒1个单位长度的速度相向而行，运动时间为t秒，其中 $0 \leq t < 10$ ．

(1)、求证：四边形EGFH是平行四边形；

(2)、若四边形EGFH为矩形，求t的值；

(3)、若点 $E^{'}$ 从E点出发沿直线AD向右运动，点 $F^{'}$ 从F点出发沿直线CB向左运动，且与点G，H以相同的速度同时出发，当四边形 $E^{'} G F^{'} H$ 为菱形时，求t的值．

查看试题解析

学生	学生一	学生二	学生三	学生四
平均数	95	96	96	95
方差	5	5	4.8	4.8

类型	进价（元/个）	零售价（元/个）
A型计算器	50	80
B型计算器	25	45