天津市五校2021-2022学年高三上学期数学期末联考试卷

试卷更新日期：2022-09-01 类型：期末考试

进入出卷网下载

一、单选题

1. 已知全集 $U = {x \in N | 0 < x < 6}$ ， $A = {3 ， 4 ， 5}$ ， $B = {2 ， 4}$ ，则 $(∁_{U} A) ∩ B =$ （）

A、 ${1 ， 2 ， 3}$ B、 ${2 ， 3 ， 4}$ C、 ${2 ， 3}$ D、{2}

查看试题解析
2. 设 $x \in R$ ，则“ $x^{2} - 3 x < 0$ ”是“ $| x - 4 | > 1$ ”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
3. 函数 $f (x) = (e^{x} + e^{- x}) l o g_{2} | x |$ 的图象大致是（）

A、 B、 C、 D、

查看试题解析
4. 某射击运动员7次的训练成绩分别为：86，88，90，89，88，87，85，则这7次成绩的第80百分位数为（）

A、88.5 B、89 C、91 D、89.5

查看试题解析
5. 已知 $f (x) = x \cdot e^{| x |}$ ， $a = f (l o g_{5} 4)$ ， $b = f (l o g_{\frac{1}{5}} \frac{1}{3})$ ， $c = f (0 . 5^{- 0.2})$ ，则 $a$ ， $b$ ， $c$ 的大小关系为（）

A、 $c > b > a$ B、 $b > c > a$ C、 $a > b > c$ D、 $c > a > b$

查看试题解析
6. 在四面体 $S - A B C$ 中， $S A ⊥$ 平面 $A B C$ ， $△ A B C$ 为正三角形，且边长为 $2 \sqrt{3}$ ， $S A = 4$ ，则该四面体的外接球的表面积是（）

A、 $\frac{25 π}{3}$ B、 $\frac{32 π}{3}$ C、 $\frac{20 \sqrt{5} π}{3}$ D、32π

查看试题解析
7. 已知双曲线 $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的左、右焦点分别为 $F_{1}$ ， $F_{2}$ ，过 $F_{2}$ 且斜率为 $- \frac{\sqrt{7}}{3}$ 的直线与双曲线在第二象限的交点为 $A$ ，若 $(\vec{F_{1} F_{2}} + \vec{F_{1} A}) \cdot \vec{F_{2} A} = 0$ ，则此双曲线的离心率为（）

A、 $\sqrt{3}$ B、 $\sqrt{2}$ C、2 D、 $\frac{2 \sqrt{3}}{3}$

查看试题解析
8. 设函数 $f (x) = c o s^{2} x - \sqrt{3} c o s (\frac{π}{2} + x) c o s (π + x) - \frac{1}{2}$ ，则下列结论错误的是（）

A、 $f (x)$ 的一个周期为 $π$ B、 $y = f (x)$ 的图象关于直线 $x = \frac{4 π}{3}$ 对称 C、将函数 $y = c o s 2 x$ 的图象向左平移 $\frac{π}{3}$ 个单位可以得到函数 $f (x)$ 的图象 D、 $f (x)$ 在 $(0 ， \frac{π}{3})$ 上单调递减

查看试题解析
9. 已知函数 $f (x) = {\begin{array}{l} c o s \frac{π x}{2} ， - 1 \leq x \leq 1 \\ - \sqrt{- x^{2} + 4 x - 3} ， 1 < x \leq 3 \end{array}$ ，若函数 $g (x) = f (x) - k (x + 1) - 1$ 恰有三个零点，则实数 $k$ 的取值范围为（）

A、 $[- \frac{3}{4} ， - \frac{1}{4}]$ B、 $(- \frac{3}{4} ， - \frac{1}{4}]$ C、 $(- \frac{4}{3} ， - \frac{1}{4})$ D、 $(- \frac{4}{3} ， - \frac{1}{4}]$

查看试题解析

二、填空题

10. 若 $i$ 为虚数单位，复数 $\frac{1 - 7 i}{{(1 + i)}^{2}}$ =.

查看试题解析
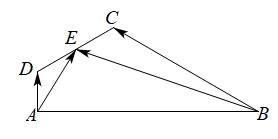
11. ${(x^{2} - \frac{2}{\sqrt{x}})}^{5}$ 展开式中，常数项为． (用数字作答)

查看试题解析
12. 已知圆心在直线 $x - 3 y = 0$ 上的圆 $C$ 与 $y$ 轴的负半轴相切，且圆 $C$ 截 $x$ 轴所得的弦长为 $4 \sqrt{2}$ ，则圆 $C$ 的方程为.

查看试题解析
13. 已知 $a > 0$ ， $b > 0$ ， $c > 1$ ，且 $a + b = 1$ ，则 $(\frac{a + 3 b}{a b} - 4) \cdot c + \frac{2 \sqrt{3}}{c - 1}$ 的最小值为.

查看试题解析
14. 为了抗击新冠肺炎疫情，现在从A医院200人和B医院100人中，按分层抽样的方法，选出6人加入“援鄂医疗队”，再从此6人中选出两人作为联络员，则这两名联络员中B医院至少有一人的概率是.设两名联络员中B医院的人数为 $X$ ，则随机变量 $X$ 的数学期望为.

查看试题解析
15. 如图，在四边形 $A B C D$ 中， $∠ B A D = 90 °$ ， $∠ A B C = 30 °$ ， $A B = 3 \sqrt{3}$ ，若 $| \vec{B C} | = 4 | \vec{A D} |$ ， $\vec{A D} \cdot \vec{B C} = 2$ ，则 $| \vec{A D} | =$ .若点 $E$ 是线段 $C D$ 上的动点，则 $\vec{A E} \cdot \vec{B E}$ 的最小值为.

查看试题解析

三、解答题

16. 在 $△ A B C$ 中，角 $A$ ， $B$ ， $C$ 所对的边分别是 $a$ ， $b$ ， $c$ ，已知 $b c o s C = (2 a - c) c o s B$ .

(1)、求角 $B$ 的大小；

(2)、设 $a = 2$ ， $c = 3$ ，求 $s i n (2 A + B)$ 的值.

查看试题解析
17. 如图，已知三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中，侧棱与底面垂直，且 $A A_{1} = A B = A C = 2$ ， $A B ⊥ A C$ ， $M$ 、 $N$ 、 $P$ 、 $D$ 分别是 $C C_{1}$ 、 $B C$ 、 $A_{1} B_{1}$ 、 $B_{1} C_{1}$ 的中点.

(1)、求证： $A C / /$ 平面 $P D N$ ；

(2)、求平面 $P M N$ 与平面 $A B C$ 夹角的余弦值；

(3)、点 $Q$ 在线段 $A_{1} B_{1}$ 上，若直线 $A M$ 与平面 $Q M N$ 所成角的正弦值为 $\frac{\sqrt{30}}{10}$ 时，求线段 $A_{1} Q$ 的长.

查看试题解析
18. 设数列 ${a_{n}}$ 的前 $n$ 项和为 $S_{n}$ ，已知首项 $a_{1} = 3$ ， $a_{n + 1} = 2 S_{n} + 3$ ，数列 ${b_{n}}$ 中， $b_{1} = 1$ ， $b_{4} = 7$ ，且满足 $b_{n + 2} = 2 b_{n + 1} - b_{n} (n \in N^{*})$

(1)、求数列 ${a_{n}}$ 和 ${b_{n}}$ 通项公式；

(2)、若 $c_{n} = \frac{b_{n}}{a_{n} - 1}$ ，求证： $\sum_{i = 1} c_{i} < \frac{3}{2}$

查看试题解析
19. 已知椭圆 $C$ ： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的离心率 $e = \frac{\sqrt{3}}{2}$ ，且椭圆 $C$ 上的点到其左焦点的最大距离为 $2 + \sqrt{3}$ ，点 $M$ 是 $x$ 轴上的一点，过点 $M$ 的直线 $l$ 与椭圆 $C$ 交于 $A$ ， $B$ 两点.

(1)、求椭圆 $C$ 的方程；

(2)、若 $△ A O M$ 的面积是 $△ B O M$ 面积的两倍，且直线 $l$ 与圆 $O$ ： $x^{2} + y^{2} = \frac{4}{7}$ 相切于点 $N$ ，求 $| M N |$ 的长.

查看试题解析
20. 已知函数 $f (x) = (x + a) (l n x - b) (b > \frac{1}{2})$ 在点 $M (e ， f (e))$ 处的切线方程为 $(e - 1) x - e y - e (e - 1) = 0$ .

(1)、求 $a$ ， $b$ ；

(2)、函数 $f (x)$ 图象与 $x$ 轴的交点为 $P$ （ $P$ 异于点 $M$ ），且在点 $P$ 处的切线方程为 $y = h (x)$ ，函数 $F (x) = f (x) - h (x)$ ， $x \in R$ ，求 $F (x)$ 的最小值；

(3)、关于 $x$ 的方程 $f (x) = m$ 有两个实数根 $x_{1}$ ， $x_{2}$ ，且 $x_{1} < x_{2}$ ，证明： $x_{2} - x_{2} \leq \frac{m e}{e - 1} + e - 1 + m$ .

查看试题解析