青海省西宁市2021-2022学年高三上学期理数期末联考试卷
试卷更新日期:2022-09-01 类型:期末考试
一、单选题
-
1. 设集合 ,则 ( )A、{2} B、{2,3} C、{-1,2,3} D、{1,2,3,4}2. 已知 =(2,3), =(3,t), =1,则 =( )A、-3 B、-2 C、2 D、33. 已知角的终边经过点 , 且 , 则( )A、 B、 C、 D、4. 曲线在点处的切线方程为( )A、 B、 C、 D、5. 在各项均为正数的等比数列中,若 , 则等于( )A、5 B、-5 C、9 D、-96. 我国古代数学家刘徽在学术研究中,不迷信古人,坚持实事求是.他对《九章算术》中“开立圆术”给出的公式产生质疑,为了证实自己的猜测,他引入了一种新的几何体“牟合方盖”:以正方体相邻的两个侧面为底做两次内切圆柱切割,然后剔除外部,剩下的内核部分.如果“牟合方盖”的主视图和左视图都是圆,则其俯视图形状为( )
 A、
A、 B、
B、 C、
C、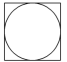 D、
D、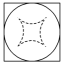 7. 设 , 为两个平面,则的充要条件是( )A、内有无数条直线与平行 B、内有两条相交直线与平行 C、 , 平行于同一条直线 D、 , 垂直于同一平面8. 设 , , , 则( )A、 B、 C、 D、9. 下列命题中为真命题的是( )A、 , B、 , C、 , D、 ,10. 函数 的图象大致为( )A、
7. 设 , 为两个平面,则的充要条件是( )A、内有无数条直线与平行 B、内有两条相交直线与平行 C、 , 平行于同一条直线 D、 , 垂直于同一平面8. 设 , , , 则( )A、 B、 C、 D、9. 下列命题中为真命题的是( )A、 , B、 , C、 , D、 ,10. 函数 的图象大致为( )A、 B、
B、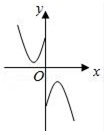 C、
C、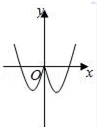 D、
D、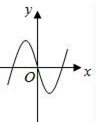 11. 已知函数( , )的单调递减区间为 , 则( )A、 B、 C、 D、12. 已知(且)恒过定点 , 且点在直线( , )上,则的最小值为( )A、 B、8 C、 D、4
11. 已知函数( , )的单调递减区间为 , 则( )A、 B、 C、 D、12. 已知(且)恒过定点 , 且点在直线( , )上,则的最小值为( )A、 B、8 C、 D、4二、填空题
-
13. 已知集合 , . 若“”是“”的充分条件,则实数的取值范围为 .14. 已知向量 , , ,则 .15. 我国南宋数学家杨辉所著的《详解九章算术》中,用图①的三角形形象地表示了二项式系数规律,俗称“杨辉三角形”.现将杨辉三角形中的奇数换成 ,偶数换成 ,得到图②所示的由数字 和 组成的三角形数表,由上往下数,记第 行各数字的和为 ,如 , , , ,……,则
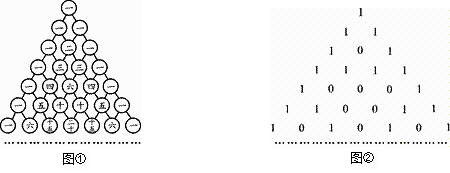 16. 的内角 的对边分别为 .若 ,则 的面积为.
16. 的内角 的对边分别为 .若 ,则 的面积为.三、解答题
-
17. 在中,内角 , , 所对的边分别为 , , , 且.(1)、证明:;(2)、若 , 且的面积为 , 求.18. 已知数列 满足 , ,设 .(1)、求 ;(2)、判断数列 是否为等比数列,并说明理由;(3)、求 的通项公式.19. 如图,在四棱锥P−ABCD中,AB//CD,且 .
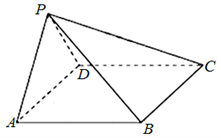 (1)、证明:平面PAB⊥平面PAD;(2)、若PA=PD=AB=DC , ,求二面角A−PB−C的余弦值.20. 设函数.
(1)、证明:平面PAB⊥平面PAD;(2)、若PA=PD=AB=DC , ,求二面角A−PB−C的余弦值.20. 设函数.(Ⅰ)求的定义域及最小正周期;
(Ⅱ)求在区间上的最值.