江西省宜春市2022届高三上学期理数期末质量检测试卷

试卷更新日期：2022-09-01 类型：期末考试

进入出卷网下载

一、单选题

1. 已知集合 $A = {x | y = l n (x - 2)} ， B = {x | x \geq - 3}$ ，则下列结论正确的是（）

A、 $A = B$ B、 $A ∩ B = \emptyset$ C、 $A \subseteq B$ D、 $B \subseteq A$

查看试题解析
2. 唐代诗人王维，字摩诘，在后世有“诗佛”之称，北宋苏轼评曰 “味摩诘之诗，诗中有画；观摩诘之画，画中有诗.”在王维《相思》这首诗中，哪一句可以作为命题（）

A、红豆生南国 B、春来发几枝 C、愿君多采撷 D、此物最相思

查看试题解析
3. 已知复数 $Z = m + i (m < 0)$ ，若 $| Z | = \sqrt{2}$ ，则 $Z^{2}$ =（）

A、2 B、-2i C、2i D、±2i

查看试题解析
4. 使得 ${(3 x + \frac{1}{\sqrt{x}})}^{n} （ n \in N^{*}$ ）的展开式中含有常数项的最小的n为（）

A、6 B、5 C、4 D、3

查看试题解析
5. 已知三棱柱 $A B C - A_{1} B_{1} C_{1}$ 为正三棱柱，且 $A A_{1} = 2 ， A B = 2 \sqrt{3}$ ， D是 $B_{1} C_{1}$ 的中点，则点B到平面 $A B_{1} D$ 的距离为（）

A、 $\frac{3}{13} \sqrt{13}$ B、 $\frac{6}{13} \sqrt{13}$ C、 $\frac{9}{13} \sqrt{13}$ D、 $\frac{12}{13} \sqrt{13}$

查看试题解析
6. 为落实国务院提出的“双减”政策，某校在课后服务时间开展了丰富多彩的兴趣小组活动，其中有个课外兴趣小组制作了一个正十二面体模型，并在十二个面分别雕刻了十二生肖的图案，作为2022年春节的吉祥物，2个兴趣小组各派一名成员将模型随机抛出，两人都希望能抛出虎的图案朝上，寓意虎虎生威.2人各抛一次，则在第一人抛出虎的图案朝上时，两人心愿均能达成的概率为（）

A、 $\frac{1}{12}$ B、 $\frac{11}{72}$ C、 $\frac{143}{144}$ D、 $\frac{23}{144}$

查看试题解析
7. 已知 $S_{△ A B C} = 3$ ，点M是△ABC内一点且 $\vec{M A} + 2 \vec{M B} = \vec{C M}$ ，则△MBC的面积为（）

A、 $\frac{1}{4}$ B、 $\frac{1}{3}$ C、 $\frac{3}{4}$ D、 $\frac{1}{2}$

查看试题解析
8. 设函数 $f (x) = x s i n x + c o s x - \frac{x^{2}}{4}$ ，则下列是函数f（x）极大值点的是（）

A、 $\frac{5}{3}$ π B、- $\frac{5}{3}$ π C、 $\frac{2}{3}$ π D、- $\frac{π}{3}$

查看试题解析
9. 若 $f (x)$ 是定义在 $R$ 的奇函数，且 $f (x + 1)$ 是偶函数，当 $0 \leq x \leq 1$ 时， $f (x) = l n (x + 1)$ ，则 $2 \leq x \leq 3$ 时 $f (x)$ 的解析式为（）

A、 $f (x) = l n (x - 1)$ B、 $f (x) = - l n (x - 1)$ C、 $f (x) = - l n (3 - x)$ D、 $f (x) = l n (3 - x)$

查看试题解析
10. 中国古代名词“刍童”原来是草堆的意思，后来用它表示上、下两个底面均为矩形（不能全为正方形且矩形的长不小于宽），四条侧棱的延长线不交于一点的六面体，关于“刍童”体积计算的描述，《九章算术》注曰：“倍上表，下表从之，亦倍下袤，上表从之各以其广乘之，并以高乘之，六而一、”其计算方法是：将上底面的长乘二，与下底面的长相加，再与上底下底面的长乘二，与上底面的长相加，再与下底面的宽相乘；把这两个数值相加，与高相乘，再取其六分之一、已知一个“刍童”的下底面是周长为10的矩形，上底面矩形的长为2，宽为1，“刍童”的高为3，则该“刍童”的体积的最大值为（）

A、12 B、 $\frac{193}{16}$ C、 $\frac{9}{4}$ D、 $\frac{9}{2}$

查看试题解析
11. 在正项等比数列 ${a_{n}$ }中，存在两项 $a_{m} ， a_{n} (m \neq n$ 且 $m ， n \in N^{*})$ ，使得 $\sqrt{a_{m} a_{n}} = 4 \sqrt{2} a_{1}$ ，且 $a_{7} = a_{6} + 2 a_{5}$ ，则 $\frac{1}{2 m - 1} + \frac{8}{n}$ 的最小值是（）

A、 $\frac{25}{13}$ B、 $\frac{25}{7}$ C、 $\frac{29}{15}$ D、 $\frac{11}{4}$

查看试题解析
12. 设点 $F_{1} ， F_{2}$ 分别为双曲线C $： \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 （ a > 0 ， b > 0 ）$ 的左右焦点，点A，B分别在双曲线C的左、右支上，若 $\vec{A B} = 5 \vec{F_{1} A}$ ， ${\vec{A F_{2}}}^{2} = \vec{A B} \cdot \vec{A F_{2}}$ ，且 $| \vec{A F_{2}} | < | \vec{B F_{2}} |$ ，则双曲线C渐近线的斜率为（）

A、 $\pm \frac{2}{5} \sqrt{15}$ B、± $\frac{2}{5} \sqrt{10}$ C、± $\frac{\sqrt{110}}{5}$ D、± $\frac{3}{5} \sqrt{10}$

查看试题解析

二、填空题

13. 已知点 $P (1 ， 2)$ 是圆C： $x^{2} + y^{2} + x - 2 y + m = 0$ 外一点，则m的取值范围为.

查看试题解析
14. 在空间直角坐标系中，点A（-1，2，-1），B（2，-1，3），点A在坐标平面xoz上的投影为点M，点B关于z轴的对称点为点N，则|MN|=

查看试题解析
15. 若方程 $s i n x + 2 c o s x + 2 - m = 0$ 在 $0 \leq x \leq \frac{π}{2}$ 时有且只有一个实数解，则m的取值范围为.

查看试题解析
16. 已知在△ABC中，角A，B，C所对的边分别为a，b，c，且 $c = 5$ ，点O为其外接圆的圆心，已知 $\vec{B O} \cdot \vec{A C} = 12$ ，则当角C取到最大值时△ABC的面积为.

查看试题解析

三、解答题

17. 在四棱台 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 底面ABCD是正方形，且侧棱 $A A_{1}$ 垂直于底面ABCD， $A A_{1} = A D = 2 A_{1} D_{1} = 4$ ， O，E分别是AC与 $D D_{1}$ 的中点.

(1)、求证：OE//平面 A₁B₁C₁D₁ ；

(2)、求直线AE与平面 A₁B₁C₁D₁ 所成角的正弦值.

查看试题解析
18. 记 $S_{n}$ 为数列 ${a_{n}}$ 的前 $n$ 项和，已知 $a_{1} = 1$ 且 $a_{n} + a_{n + 2} = 2 a_{n + 1}$ 对任意 $n \in N^{*}$ 恒成立，从以下三个条件中任选一个：① $S_{9} = 81$ ；② $a_{3} + a_{9} = 22$ ；③ $\frac{S_{5}}{5} - \frac{S_{2}}{2} = 3$ .

(1)、求数列 ${a_{n}}$ 的通项公式；

(2)、求数列 ${a_{n}}$ 的前 $n$ 项和 $S_{n}$ ；

(3)、利用下面求 $S = 1 + 2 + 3 + ⋯ + n$ 的方法，求数列 ${S_{n}}$ 的前 $n$ 项和 $T_{n}$ .
$∵ n^{2} - {(n - 1)}^{2} = 2 n - 1$ ，
$1^{2} - 0^{2} = 2 \times 1 - 1$ ， $2^{2} - 1^{2} = 2 \times 2 - 1$ ， $3^{2} - 2^{2} = 2 \times 3 - 1$ ， $⋯$ ， $n^{2} - {(n - 1)}^{2} = 2 n - 1$ ，
以上 $n$ 个等式相加得 $n^{2} = 2 S - n$ ， $∴ S_{n} = \frac{n^{2} + n}{2}$ .

查看试题解析
19. 在△ABC中，角A，B，C所对的边分别为a，b，c，且 $a = \sqrt{3} ， c o s B = \frac{\sqrt{3}}{c} - \frac{b}{2 c}$ .

(1)、求角C的大小；

(2)、若角C的平分线交AB于点D，且 $C D = 1$ ，求b的值.

查看试题解析
20. 某企业从生产的一批零件中抽取100件产品作为样本，检测其质量指标值m（其中： $100 \leq m \leq 400$ ，得到频率分布并依据质量指标值划分等级如表所示：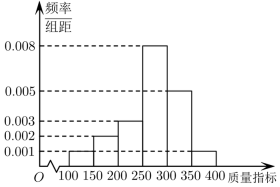
质量指标值m
50≤m<350
100≤m<150或350≤m≤400
等级
A级
B级

(1)、根据频率分布直方图估计产品的质量指标值的中位数；

(2)、从样本的B级零件中随机抽3件，记其中质量指标值在[350，400]的零件的件数为 $ξ$ ，求 $ξ$ 的分布列和数学期望；

(3)、该企业为节省检测成本，采用混装的方式将所有的零件按500个一箱包装，已知一个A级零件的利润是10元，一个B级零件的利润是5元，以样本分布的频率作为总体分布的概率，试估计每箱零件的利润.

查看试题解析
21. 已知圆 $O_{1} ： {(x + 1)}^{2} + y^{2} = 8$ 上有一动点 $Q$ ，点 $O_{2}$ 的坐标为 $(1 ， 0)$ ，四边形 $Q O_{1} O_{2} R$ 为平行四边形，线段 $O_{1} R$ 的垂直平分线交 $O_{2} R$ 于点 $P$ .
（Ⅰ）求点 $P$ 的轨迹 $C$ 的方程；
（Ⅱ）过点 $O_{2}$ 作直线与曲线 $C$ 交于 $A ， B$ 两点，点 $K$ 的坐标为 $(2 ， 1)$ ，直线 $K A ， K B$ 与 $y$ 轴分别交于 $M ， N$ 两点，求证：线段 $M N$ 的中点为定点，并求出 $△ K M N$ 面积的最大值.

查看试题解析
22. 已知函数 $f (x) = e^{x - 1} - a (x + 1)$ ， g $(x) = l n x$ .

(1)、求 $g (x)$ 在点 $(1 ， 0)$ 处的切线方程；

(2)、讨论 $f (x)$ 的单调性；

(3)、当 $a = \frac{1}{2} ， x \in (1 ， + \infty)$ 时，求证： $f (x) > (x - 1) g (x)$ .

查看试题解析

质量指标值m	50≤m<350	100≤m<150或350≤m≤400
等级	A级	B级