河北省石家庄市行唐县2022届高三上学期数学期末考试试卷

试卷更新日期：2022-09-01 类型：期末考试

进入出卷网下载

一、单选题

1. 已知全集 $U = {1 ， 2 ， 3 ， 4 ， 5}$ ，集合 $M = {1 ， 2 ， 3 ， 4} ， N = {3 ， 4 ， 5}$ ，则 $∁_{U} (M ∩ N) =$ （）

A、{5} B、 ${1 ， 2}$ C、 ${3 ， 4}$ D、 ${1 ， 2 ， 5}$

查看试题解析
2. 设 $i^{3} z = 3 + 5 i$ ，则 $z =$ （）

A、 $- 5 + 3 i$ B、 $- 5 - 3 i$ C、 $5 - 3 i$ D、 $5 + 3 i$

查看试题解析
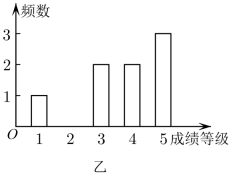
3. 等比数列 ${a_{n}}$ 的前 $n$ 项和为 $S_{n}$ ， $S_{3} = 3$ ， $S_{6} = 9$ ，则公比 $q =$ （）

A、 $\sqrt{3}$ B、 $\sqrt{2}$ C、 $\sqrt[3]{3}$ D、 $\sqrt[3]{2}$

查看试题解析
4. 某高校甲､乙两位同学大学四年选修课程的考试成绩等级（选修课的成绩等级分为1，2，3，4，5，共五个等级）的条形图如图所示，则甲成绩等级的中位数与乙成绩等级的众数分别是（）

A、3，5 B、3，3 C、3.5，5 D、3.5，4

查看试题解析
5. 已知一个圆锥的体积为 $3 π$ ，任取该圆锥的两条母线a，b，若a，b所成角的最大值为 $\frac{π}{3}$ ，则该圆锥的侧面积为（）

A、 $3 \sqrt{3} π$ B、6π C、 $6 \sqrt{3} π$ D、9π

查看试题解析
6. 已知椭圆 $E ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的左顶点和上顶点分别为 $A ， B$ ，若 $A B$ 的垂直平分线过 $E$ 的下顶点 $C$ ，则 $E$ 的离心率为（）

A、 $\frac{\sqrt{6}}{3}$ B、 $\frac{\sqrt{3}}{3}$ C、 $\frac{\sqrt{2}}{3}$ D、 $\frac{1}{3}$

查看试题解析
7. 酒驾是严重危害交通安全的违法行为.根据国家有关规定：100 $m L$ 血液中酒精含量在20~80 $m g$ 之间为酒后驾车，80 $m g$ 及以上为醉酒驾车.假设某驾驶员喝了一定量的酒后，其血液中的酒精含量上升到了1.2 $m g / m L$ ，且在停止喝酒以后，他血液中的酒精含量会以每小时20%的速度减少，若他想要在不违法的情况下驾驶汽车，则至少需经过的小时数约为（）（参考数据： $l g 2 \approx 0.3$ ， $l g 3 \approx 0.48$ ）

A、6 B、7 C、8 D、9

查看试题解析
8. 已知实数a，b满足 $a^{3} + e^{a} = e^{- a} + 1$ ， $b^{3} + e^{b} = e^{- b} - 1$ ，则 $a + b =$ （）

A、-2 B、0 C、1 D、2

查看试题解析

二、多选题

9. 下列式子等于 $c o s (x - \frac{π}{6})$ 的是（）

A、 $c o s (x - \frac{5 π}{6})$ B、 $s i n (x - \frac{2 π}{3})$ C、 $\frac{\sqrt{3} c o s x + s i n x}{2}$ D、 $2 c o s^{2} (\frac{π}{12} - \frac{x}{2}) - 1$

查看试题解析
10. 设 $a > 0$ ， $b > 0$ ，且 $a \neq b$ ，则“ $a + b > 2$ ”的一个必要条件可以是（）

A、 $a^{3} + b^{3} > 2$ B、 $a^{2} + b^{2} > 2$ C、 $a b > 1$ D、 $\frac{1}{a} + \frac{1}{b} > 2$

查看试题解析
11. 若函数 $y = f (x)$ 的图象上存在两点，使得 $f (x)$ 的图象在这两点处的切线互相垂直，则称 $y = f (x)$ 具有T性质.下列函数中具有T性质的是（）

A、 $y = s i n^{2} x$ B、 $y = t a n x$ C、 $y = | \frac{x - 1}{x + 2} |$ ， $x \in (- 2 ， + \infty)$ D、 $y = e^{x} - l n x$

查看试题解析
12. 已知定义在 $[0 ， \frac{π}{4}]$ 上的函数 $f (x) = s i n (ω x - \frac{π}{4}) (ω > 0)$ （）

A、若 $f (x)$ 恰有两个零点，则 $ω$ 的取值范围是 $[5 ， 9)$ B、若 $f (x)$ 恰有两个零点，则 $ω$ 的取值范围是 $(5 ， 9]$ C、若 $f (x)$ 的最大值为 $\frac{ω}{5}$ ，则 $ω$ 的取值个数最多为2 D、若 $f (x)$ 的最大值为 $\frac{ω}{5}$ ，则 $ω$ 的取值个数最多为3

查看试题解析

三、填空题

13. 已知平面向量 $\vec{a}$ ， $\vec{b}$ 满足 $| \vec{a} | = | \vec{b} | = \frac{\sqrt{2} | \vec{a} + \vec{b} |}{2}$ ，则 $\vec{a}$ 与 $\vec{b}$ 夹角的大小为.

查看试题解析
14. 将五枚质地､大小完全一样的硬币向上抛出，则正面向上的硬币枚数为2或者3的概率为.

查看试题解析
15. 根据抛物线的光学性质可知，从抛物线的焦点发出的光线经该抛物线反射后与对称轴平行，一条平行于对称轴的光线经该抛物线反射后会经过抛物线的焦点.如图所示，从 $A (5 ， m_{1})$ 沿直线 $y = m_{1}$ 发出的光线经抛物线 $y^{2} = 4 x$ 两次反射后，回到光源接收器 $D (5 ， m_{2})$ ，则该光线经过的路程为.

查看试题解析
16. 已知 $P$ 为正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 表面上的一个动点， $A B = 2$ ， $M$ 是棱 $A B$ 延长线上的一点，且 $\vec{A B} = \vec{B M}$ ，若 $P M = 2 \sqrt{2}$ ，则动点 $P$ 运动轨迹的长为.

查看试题解析

四、解答题

17. 已知在数列 ${a_{n}}$ 中， $a_{1} = 1$ ， $a_{3} = \frac{1}{3}$ ，且该数列满足 $\frac{2}{a_{n + 1}} = \frac{a_{n + 2} + a_{n}}{a_{n} a_{n + 2}}$ .

(1)、求 ${a_{n}}$ 的通项公式；

(2)、已知 $S_{n}$ 是数列 ${b_{n}}$ 的前n项和，且 $b_{n} = {(- 1)}^{n} (a_{n} + a_{n + 1})$ ，求 $S_{2 n}$ .

查看试题解析
18. $△ A B C$ 的内角A，B，C的对边分别为a，b，c.已知 $c^{2} + b^{2} c o s^{2} A = 2 b c c o s A$ .

(1)、求B.

(2)、_________，若问题中的三角形存在，试求出 $c o s C$ ；若问题中的三角形不存在，请说明理由.
在① $a = \frac{\sqrt{3}}{3} b + \frac{\sqrt{3}}{3} c$ ， ② $b = \frac{1}{2} a + \frac{\sqrt{3}}{2} c$ ， ③ $c = \frac{\sqrt{2}}{2} b - \frac{\sqrt{2}}{2} a$ 这三个条件中任选一个，补充在横线上.

注：如果选择多个条件分别解答，按第一个解答计分.

查看试题解析
19. 为了调查某苹果园中苹果的生长情况，在苹果园中随机采摘了100个苹果.经整理分析后发现，苹果的重量 $x$ （单位： $k g$ ）近似服从正态分布 $N (0.4 ， σ^{2})$ ，如图所示，已知 $P (x < 0.1) = 0.1$ ， $P (x < 0.3) = 0.3$ .

(1)、若从苹果园中随机采摘1个苹果，求该苹果的重量在 $(0.5 ， 0.7]$ 内的概率；

(2)、从这100个苹果中随机挑出8个，这8个苹果的重量情况如下.
重量范围（单位： $k g$ ）
$[0.1 ， 0.3)$
$[0.3 ， 0.5)$
$[0.5 ， 0.7]$
个数
2
4
2
为进一步了解苹果的甜度，从这8个苹果中随机选出3个，记随机选出的3个苹果中重量在 $[0.3 ， 0.7]$ 内的个数为 $X$ ，求随机变量 $X$ 的分布列和数学期望.

查看试题解析
20. 如图，在多面体ABCEF中， $△ A B C$ 和 $△ A C E$ 均为等边三角形，D是AC的中点， $E F / / B D$ ．

(1)、证明： $A C ⊥ B F$ ．

(2)、若平面 $A B C ⊥$ 平面ACE，求二面角 $A - B C - E$ 的余弦值.

查看试题解析
21. 已知函数 $f (x) = a x^{2} + c o s x$ .

(1)、当 $a = \frac{1}{2}$ 时，讨论 $f (x)$ 的单调性；

(2)、当 $x \geq 0$ 时， $f (x) \geq 1$ ，求a的取值范围.

查看试题解析
22. 如图，已知双曲线 $C ： \frac{x^{2}}{3} - y^{2} = 1$ ，过 $P (1 ， 1)$ 向双曲线 $C$ 作两条切线，切点分别为 $A (x_{1} ， y_{1})$ ， $B (x_{2} ， y_{2})$ ，且 $x_{1} < 0 ， x_{2} > 0$ .

(1)、证明：直线 $P A$ 的方程为 $\frac{x_{1} x}{3} - y_{1} y = 1$ .

(2)、设 $F$ 为双曲线 $C$ 的左焦点，证明： $∠ A F P + ∠ B F P = π$ .

查看试题解析

重量范围（单位： $k g$ ）	$[0.1 ， 0.3)$	$[0.3 ， 0.5)$	$[0.5 ， 0.7]$
个数	2	4	2