广西壮族自治区玉林市容县2021-2022学年七年级下学期期末数学试题

试卷更新日期：2022-09-01 类型：期末考试

进入出卷网下载

一、选择题：本大题共12小题，每小题3分，共36分.

1. 下列各数中，是无理数的是（）

A、 $\frac{10}{3}$ B、 $\sqrt{10}$ C、 $\sqrt{4}$ D、 $\sqrt[3]{64}$

查看试题解析
2. 为了了解一批产品的质量，从中抽取200个产品进行检查。请问被抽查的200个产品的质量叫做（）

A、总体 B、个体 C、总体的一个样本 D、样本容量

查看试题解析
3. 已知坐标平面内的点 $A (3 ， - 2)$ ，把它向下平移4个单位长度，再向左平移2个单位长度，则点 $A$ 的坐标变为（）

A、 $(1 ， - 6)$ B、 $(- 5 ， - 3)$ C、 $(5 ， 2)$ D、 $(- 1 ， 2)$

查看试题解析
4. 已知 ${\begin{cases} x = 3 \\ y = 1 \end{cases}$ 是关于 $x$ ， $y$ 的二元一次方程 $a x - 4 y = 2$ 的一个解，则 $a$ 的值是（）

A、2 B、－2 C、3 D、－3

查看试题解析
5. 下列说法正确的是（）

A、 $6 - \sqrt{5}$ 的整数部分是4 B、两个实数的和一定是实数 C、－4是 $\sqrt{16}$ 的平方根 D、立方根等于本身的数是0和1

查看试题解析
6. 如图，直线 $a ∥ b$ ，直线 $c$ 与直线 $a$ ， $b$ 分别交于点 $D$ 、 $E$ ，射线 $D F ⊥$ 直线 $c$ ，则图中与 $∠ 1$ 互余的角有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
7. 一组数据的最大值是97，最小值是76，若组距是4，则可分为（）

A、4组 B、5组 C、6组 D、7组

查看试题解析
8. 如果 $a > b$ ， $c < 0$ ，那么下列不等式成立的是 $($ 　　 $)$

A、 $a + c > b$ B、 $a + c > b - c$ C、 $a c - 1 > b c - 1$ D、 $a (c - 1) < b (c - 1)$

查看试题解析
9. 若关于 $x$ ， $y$ 的二元一次方程组 ${\begin{array}{l} x - y = 2 m + 1 \\ x + 3 y = 3 \end{array}$ 的解满足 $x + y > 0$ ，则 $m$ 的取值范围是（）

A、 $m > 2$ B、 $m > - 2$ C、 $m < 2$ D、 $m < - 2$

查看试题解析
10. 小华去商店购买 $A$ 、 $B$ 两种玩具，共用了12元， $A$ 种玩具每件1元， $B$ 种玩具每件3元.若每种玩具至少买一件，且 $A$ 种玩具的数量不少于 $B$ 种玩具的数量，则小华的购买方案有（）

A、7种 B、6种 C、4种 D、3种

查看试题解析
11. 下列各数轴上表示 $x$ 的取值范围可能是不等式组 ${\begin{array}{l} x + 2 > m \\ (2 m - 1) x - 6 < 0 \end{array}$ 的解集的是（）

A、 B、 C、 D、

查看试题解析
12. 在平面直角坐标系中，对 $P (x ， y)$ 作变换得到 $P^{'} (- y + 1 ， x + 1)$ ，例如： $A_{1} (3 ， 2)$ 作上述变换得到 $A_{2} (- 1 ， 4)$ ，再将 $A_{2}$ 作上述变换得到 $A_{3} (- 3 ， 0)$ ，这样依次得到 $A_{1}$ ， $A_{2}$ ， $A_{3}$ ， …， $A_{n}$ ， …，则 $A_{2022}$ 的坐标为（）

A、 $(- 1 ， 4)$ B、 $(3 ， 2)$ C、 $(- 3 ， 0)$ D、 $(1 ， - 2)$

查看试题解析

二、填空题：本大题共6小题，每小题3分，共18分.

13. 调查“神舟十三号载人飞船”的各零件合格情况，宜采用调查（填“全面”或“抽样”）.

查看试题解析
14. 如图所示，关于x的不等式的解集为.

查看试题解析
15. 在平面直角坐标系中，点 $P (1 - \sqrt{2} ， - 1)$ 到 $y$ 轴的距离是.

查看试题解析
16. 如图， $∠ 3 = 38 °$ ，直线 $b$ 平移后得到直线 $a$ ，则 $∠ 1 + ∠ 2 =$ $°$ .

查看试题解析
17. 如图， $A B ∥ C D$ ， $B F$ 、 $D F$ 分别平分 $∠ A B E$ 和 $∠ C D E$ ， $B F ∥ D E$ ， $∠ F$ 与 $∠ A B E$ 互补，则 $∠ F$ 的度数为 $°$ .

查看试题解析
18. 已知关于 $x$ ， $y$ 的方程组 ${\begin{cases} a x + 3 y = 12 \\ x - 3 y = 0 \end{cases}$ 的解为整数，且关于 $x$ 的不等式组 ${\begin{cases} 2 (x + 1) < x + 5 \\ 3 x > a - 4 \end{cases}$ 有且仅有3个整数解，则所有满足条件的整数a的和为.

查看试题解析

三、解答题：本大题共8小题，满分共66分.

19. 计算： $\sqrt[3]{64} - \sqrt{{(- 6)}^{2}} - | \sqrt{3} - 2 | + 2 \sqrt{3}$

查看试题解析
20. 解方程组 ${\begin{array}{l} 3 x + 2 y = 1 \\ 2 x - 3 y = 5 \end{array}$

查看试题解析
21. 解不等式组 ${\begin{cases} \frac{x - 3}{2} + 2 \geq x \\ 3 (x - 1) > x - 8 \end{cases}$ ，在数轴上表示出解集，并写出该不等式组的非负整数解.

查看试题解析
22. 某学校的平面示意图如图所示，若实验楼所在的位置的坐标为 $(- 2 ， - 3)$ .

(1)、请你根据题意，画出平面直角坐标系.若办公楼的位置是 $(- 4 ， - 2)$ ，则在图中标出办公楼的位置；

(2)、请写出校门、图书楼、教学楼所在位置的坐标；

(3)、若图中小方格的连长的实际长度是不等式 $5 x - 3 < 3 x + 15$ 的最大整数解（单位：米），请求出办公楼到图书楼的实际距离.

查看试题解析
23. 为了了解学生寒假阅读情况，开学初学校进行了问卷调查，并对部分学生假期（24天）的阅读总时间作了随机抽样分析，设被抽样的每位同学寒假阅读的总时间为 $t$ （小时），阅读总时间分为四个类别： $A (0 \leq t < 12)$ ， $B (12 \leq t < 24)$ ， $C (24 \leq t < 36)$ ， $D (t \geq 36)$ ，将分类结果制成两幅统计图（尚不完整）.根据以上信息，回答下列问题：

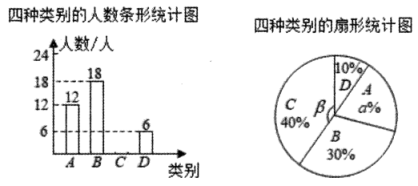(1)、本次抽样的样本容量为；

(2)、扇形图中 $a$ 的值为，圆心角 $β$ 的度数为；

(3)、补全条形统计图；

(4)、若该校有3000名学生，估计寒假阅读的总时间少于24小时的学生有多少名？

查看试题解析
24. 如图， $A D$ 平分 $∠ B A C$ 交 $B C$ 于点 $D$ ，点 $F$ 在 $B A$ 的延长线上，点 $E$ 在线段 $C D$ 上， $E F$ 与 $A C$ 相交于点 $G$ ， $∠ B D A + ∠ C E G = 180 °$ .

(1)、 $A D$ 与 $E F$ 平行吗？请说明理由；

(2)、若点 $H$ 在 $F E$ 的延长线上，且 $∠ E D H = ∠ C$ ， $∠ F = 49 °$ ，求 $∠ H$ 的度数.

查看试题解析
25. 某中学准备购进 $A$ 、 $B$ 两种教学用具共40件， $A$ 种每件价格比 $B$ 种每件贵6元，同时购进3件 $A$ 种教学用具和2件 $B$ 种教学用具恰好用去113元.

(1)、求购买5件 $A$ 和8件 $B$ 两种教学用具共用了多少元？

(2)、学校准备用不少于830元且不多于850元的金额购买 $A$ 、 $B$ 两种教学用具，问至少能购买多少件 $A$ 种教学用具？

查看试题解析
26. 如图，在平面直角坐标系 $x O y$ 中，已知 $A (8 ， 0)$ ，将线段 $O A$ 平移至 $C B$ ，点 $D$ 在 $x$ 轴正半轴上， $C (a ， b)$ ，且 $\sqrt{a + b - 10} + | b - 6 | = 0$ .连接 $O C$ ， $A B$ ， $C D$ ， $B D$ .

(1)、求出点 $C$ 和点 $B$ 的坐标；

(2)、当 $△ O D C$ 的面积是 $△ A B D$ 的面积的3倍时，求点 $D$ 的坐标；

(3)、设 $∠ O C D = α$ ， $∠ D B A = β$ ， $∠ B D C = θ$ ，判断 $α$ 、 $β$ 、 $θ$ 之间的数量关系，并说明理由.

查看试题解析