浙江省衢州市2022年中考数学试卷
试卷更新日期:2022-09-01 类型:中考真卷
一、选择题(本题共有10小题,每小题3分,共30分)
-
1. 下列图形是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 计算结果等于2的是( )A、 B、 C、 D、3. 在平面直角坐标系中,点 位于A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 如图是某品牌运动服的S号,M号,L号,XL号的销售情况统计图,则厂家应生产最多的型号为( )
2. 计算结果等于2的是( )A、 B、 C、 D、3. 在平面直角坐标系中,点 位于A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 如图是某品牌运动服的S号,M号,L号,XL号的销售情况统计图,则厂家应生产最多的型号为( ) A、S号 B、M号 C、L号 D、XL号5. 线段a、b、c首尾顺次相接组成三角形,若a=1,b=3,则c的长度可以是( )A、3 B、4 C、5 D、66. 某班环保小组收集废旧电池,数据统计如下表.问1节5号电池和1节7号电池的质量分别是多少?设1节5号电池的质量为x克,1节7号电池的质量为y克,列方程组,由消元法可得x的值为( )
A、S号 B、M号 C、L号 D、XL号5. 线段a、b、c首尾顺次相接组成三角形,若a=1,b=3,则c的长度可以是( )A、3 B、4 C、5 D、66. 某班环保小组收集废旧电池,数据统计如下表.问1节5号电池和1节7号电池的质量分别是多少?设1节5号电池的质量为x克,1节7号电池的质量为y克,列方程组,由消元法可得x的值为( )5号电池(节)
7号电池(节)
总质量(克)
第一天
2
2
72
第二天
3
2
96
A、12 B、16 C、24 D、267. 不等式组 , 的解集是( )A、 B、无解 C、 D、8. 西周数学家商高总结了用“矩”(如图1)测量物高的方法:把矩的两边放置成如图2的位置,从矩的一端A(人眼)望点E,使视线通过点C,记人站立的位置为点B,量出BG长,即可算得物高EG.令BG=x(m), EG=y(m),若a=30cm,b=60cm,AB=1.6m,则y关于x的函数表达式为( )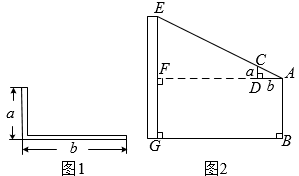 A、 B、 C、 D、9. 如图,在△ABC中,AB=AC,∠B=36°.分别以点A,C为圆心,大于的长为半径画弧,两弧相交于点D,E,作直线DE分别交AC,BC于点F,G.以G为圆心,GC长为半径画弧,交BC于点H,连结AG,AH.则下列说法错误的是( )
A、 B、 C、 D、9. 如图,在△ABC中,AB=AC,∠B=36°.分别以点A,C为圆心,大于的长为半径画弧,两弧相交于点D,E,作直线DE分别交AC,BC于点F,G.以G为圆心,GC长为半径画弧,交BC于点H,连结AG,AH.则下列说法错误的是( ) A、 B、 C、 D、10. 已知二次函数 , 当时,y的最小值为 , 则a的值为( )A、或4 B、或 C、或4 D、或4
A、 B、 C、 D、10. 已知二次函数 , 当时,y的最小值为 , 则a的值为( )A、或4 B、或 C、或4 D、或4二、填空题(本题共有6小题,每小题4分,共24分)
-
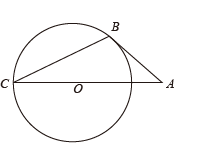
11. 计算: .12. 不透明袋子里装有仅颜色不同的 4 个白球和2个红球,从袋子中随机摸出一球,“摸出红球”的概率是 .13. 如图,AB切⊙O于点 , AO的延长线交⊙O于点C,连接BC,若∠A=40°,则∠C的度数为 .
 14. 将一个容积为360cm3的包装盒剪开铺平,纸样如图所示.利用容积列出图中x(cm)满足的一元二次方程:(不必化简).
14. 将一个容积为360cm3的包装盒剪开铺平,纸样如图所示.利用容积列出图中x(cm)满足的一元二次方程:(不必化简).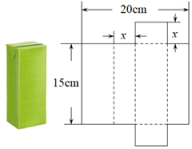 15. 如图,在△ABC中,边AB在x轴上,边AC交y轴于点E.反比例函数的图象恰好经过点C,与边BC交于点D.若AE=CE,CD=2BD, , 则k= .
15. 如图,在△ABC中,边AB在x轴上,边AC交y轴于点E.反比例函数的图象恰好经过点C,与边BC交于点D.若AE=CE,CD=2BD, , 则k= .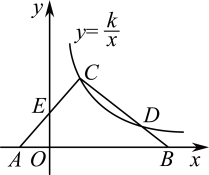 16. 希腊数学家海伦给出了挖掘直线隧道的方法:如图,A,B是两侧山脚的入口,从B出发任作线段BC,过C作CD⊥BC,然后依次作垂线段DE,EF,FG,GH,直到接近点A,作AJ⊥GH于点J.每条线段可测量,长度如图所示.分别在BC,AJ上任选点M,N,作MQ⊥BC,NP⊥AJ,使得 , 此时点P,A,B,Q共线.挖隧道时始终能看见P,Q处的标志即可.
16. 希腊数学家海伦给出了挖掘直线隧道的方法:如图,A,B是两侧山脚的入口,从B出发任作线段BC,过C作CD⊥BC,然后依次作垂线段DE,EF,FG,GH,直到接近点A,作AJ⊥GH于点J.每条线段可测量,长度如图所示.分别在BC,AJ上任选点M,N,作MQ⊥BC,NP⊥AJ,使得 , 此时点P,A,B,Q共线.挖隧道时始终能看见P,Q处的标志即可. (1)、 km.(2)、 = .
(1)、 km.(2)、 = .三、解答题(本题共有8小题,第17~19小题每小题6分,第20~21小题每小题8分,第22~23小题每小题10分,第24小题12分,共66分,请务必写出解答过程)
-
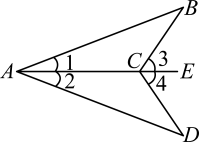
17.(1)、因式分解: .(2)、化简: .18. 已知:如图, . 求证: .
 19. 如图,在4×4的方格纸中,点A,B在格点上.请按要求画出格点线段(线段的端点在格点上),并写出结论.
19. 如图,在4×4的方格纸中,点A,B在格点上.请按要求画出格点线段(线段的端点在格点上),并写出结论.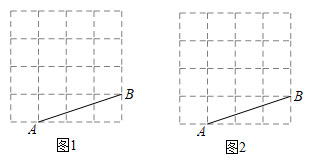 (1)、在图1中画一条线段垂直AB.(2)、在图2中画一条线段平分AB.20. 如图,C,D是以AB为直径的半圆上的两点, , 连结BC,CD.
(1)、在图1中画一条线段垂直AB.(2)、在图2中画一条线段平分AB.20. 如图,C,D是以AB为直径的半圆上的两点, , 连结BC,CD. (1)、求证: .(2)、若 , , 求阴影部分的面积.21. 【新知学习】在气象学上,“入夏”由两种平均气温与22℃比较来判断:
(1)、求证: .(2)、若 , , 求阴影部分的面积.21. 【新知学习】在气象学上,“入夏”由两种平均气温与22℃比较来判断:衢州市2021年5月5日~5月14日的两种平均气温统计表 (单位:℃)

注:“五天滑动平均气温”指某一天及其前后各两天的日平均气温的平均数,如:
(℃).
已知2021年的从5月8日起首次连续五天大于或等于22℃,而对应着~ , 其中第一个大于或等于22℃的是 , 则5月7日即为我市2021年的“入夏日”.
【新知应用】已知我市2022年的“入夏日”为下图中的某一天,请根据信息解决问题:
衢州市2022年5月24日~6月2日的两种平均气温折线统计图
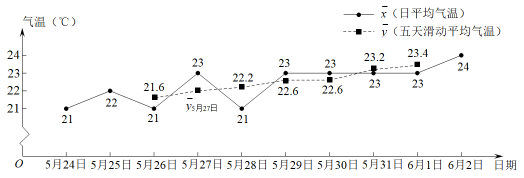 (1)、求2022年的.(2)、写出从哪天开始,图中的连续五天都大于或等于22℃.并判断今年的“入夏日”.(3)、某媒体报道:“夏天姗姗来迟,衢州2022年的春天比去年长.”你认为这样的说法正确吗?为什么?(我市2021年和2022年的入春时间分别是2月1日和2月27日)22. 金师傅近期准备换车,看中了价格相同的两款国产车.
(1)、求2022年的.(2)、写出从哪天开始,图中的连续五天都大于或等于22℃.并判断今年的“入夏日”.(3)、某媒体报道:“夏天姗姗来迟,衢州2022年的春天比去年长.”你认为这样的说法正确吗?为什么?(我市2021年和2022年的入春时间分别是2月1日和2月27日)22. 金师傅近期准备换车,看中了价格相同的两款国产车.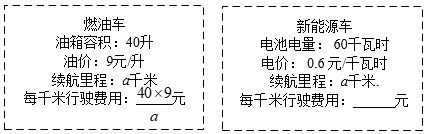 (1)、用含a的代数式表示新能源车的每千米行驶费用.(2)、若燃油车的每千米行驶费用比新能源车多0.54元.
(1)、用含a的代数式表示新能源车的每千米行驶费用.(2)、若燃油车的每千米行驶费用比新能源车多0.54元.①分别求出这两款车的每千米行驶费用.
②若燃油车和新能源车每年的其它费用分别为4800元和7500元.问:每年行驶里程为多少千米时,买新能源车的年费用更低?(年费用=年行驶费用+年其它费用)
23. 如图1为北京冬奥会“雪飞天”滑雪大跳台赛道的横截面示意图.取水平线OE为x轴,铅垂线OD为y轴,建立平面直角坐标系.运动员以速度从D点滑出,运动轨迹近似抛物线 . 某运动员7次试跳的轨迹如图2.在着陆坡CE上设置点K(与DO相距32m)作为标准点,着陆点在K点或超过K点视为成绩达标.(参考数据: , )
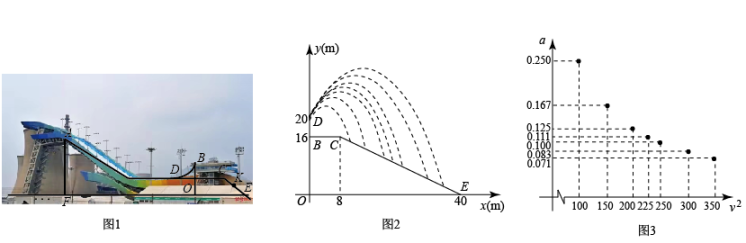 (1)、求线段CE的函数表达式(写出的取值范围).(2)、当时,着陆点为P,求P的横坐标并判断成绩是否达标.(3)、在试跳中发现运动轨迹与滑出速度v的大小有关,进一步探究,测算得7组a与 的对应数据,在平面直角坐标系中描点如图3.
(1)、求线段CE的函数表达式(写出的取值范围).(2)、当时,着陆点为P,求P的横坐标并判断成绩是否达标.(3)、在试跳中发现运动轨迹与滑出速度v的大小有关,进一步探究,测算得7组a与 的对应数据,在平面直角坐标系中描点如图3.①猜想a关于的函数类型,求函数表达式,并任选一对对应值验证.
②当v为多少m/s时,运动员的成绩恰能达标(精确到1m/s)?
24. 如图,在菱形ABCD中,AB=5,BD为对角线.点E是边AB延长线上的任意一点,连结DE交BC于点F,BG平分∠CBE交DE于点G. (1)、求证:.(2)、若 .
(1)、求证:.(2)、若 .①求菱形的面积.
②求的值.
(3)、若 , 当的大小发生变化时(),在AE上找一点T,使GT为定值,说明理由并求出ET的值.