江苏省宜兴市丁蜀学区2021-2022学年八年级上学期第一次质量调研考试数学试卷
试卷更新日期:2022-09-01 类型:月考试卷
一、单选题
-
1. 下列说法正确的是( )A、全等三角形是指形状相同的两个三角形 B、全等三角形是指面积相等的两个三角形 C、两个等边三角形是全等三角形 D、全等三角形是指两个能完全重合的三角形2. 下列图案是几种名车的标志,请你指出,在这几个图案中是轴对称图形的共有( )
 A、1个 B、2个 C、3个 D、4个3. 如图是由4个相同的小正方形组成的网格图,其中∠1+∠2等于( )
A、1个 B、2个 C、3个 D、4个3. 如图是由4个相同的小正方形组成的网格图,其中∠1+∠2等于( )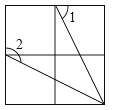 A、150° B、180° C、210° D、225°4. 如图, , 若 , , 则的度数为( )
A、150° B、180° C、210° D、225°4. 如图, , 若 , , 则的度数为( ) A、 B、 C、 D、5. 如图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B到C的方向平移到△DEF的位置,AB=10,DO=4,平移距离为6,则阴影部分面积为( )
A、 B、 C、 D、5. 如图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B到C的方向平移到△DEF的位置,AB=10,DO=4,平移距离为6,则阴影部分面积为( )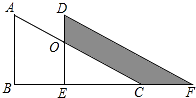 A、48 B、96 C、84 D、426. 如图,已知∠ABC=∠DCB,下列所给条件不能证明△ABC≌△DCB的是( )
A、48 B、96 C、84 D、426. 如图,已知∠ABC=∠DCB,下列所给条件不能证明△ABC≌△DCB的是( )
A、∠A=∠D B、AB=DC C、∠ACB=∠DBC D、AC=BD7. 如图,∠C=∠D=90°,若添加一个条件,可使用“HL”判定Rt△ABC与Rt△ABD全等,则以下给出的条件适合的是( ) A、AC=AD B、AB=AB C、∠ABC=∠ABD D、∠BAC=∠BAD8. 如图,正五边形中,F为边中点,连接 , 则的度数是( )
A、AC=AD B、AB=AB C、∠ABC=∠ABD D、∠BAC=∠BAD8. 如图,正五边形中,F为边中点,连接 , 则的度数是( )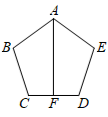 A、 B、 C、 D、9. 如图,过边长为1的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连PQ交AC边于D,则DE的长为( )
A、 B、 C、 D、9. 如图,过边长为1的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连PQ交AC边于D,则DE的长为( )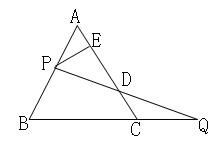 A、 B、 C、 D、不能确定10. 如图,在中,以为腰作等腰直角三角形和等腰直角三角形 , 连接为边上的高线,延长交于点 , 下列结论①;②;③;④ , 其中正确的有( )
A、 B、 C、 D、不能确定10. 如图,在中,以为腰作等腰直角三角形和等腰直角三角形 , 连接为边上的高线,延长交于点 , 下列结论①;②;③;④ , 其中正确的有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 下列图形:①角;②直角三角形;③等边三角形;④线段;⑤等腰三角形;⑥平行四边形.其中一定是轴对称图形的有个.
12. 已知,如图,AD=AC,BD=BC,O为AB上一点,那么图中共有对全等三角形.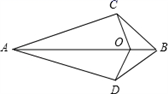 13. 如图,在△ABC中,AB=AC,AD是BC边上的高,点E、F是AD的三等分点,若△BEF的面积为12,则图中阴影面积为 .
13. 如图,在△ABC中,AB=AC,AD是BC边上的高,点E、F是AD的三等分点,若△BEF的面积为12,则图中阴影面积为 . 14. 将一张长方形纸条折成如图的形状,已知 , 则°.
14. 将一张长方形纸条折成如图的形状,已知 , 则°. 15. 如图,点D在边BC上,DE⊥AB,DF⊥BC,垂足分别为点E,D,BD=CF,BE=CD.若∠AFD=155°,则∠EDF= .
15. 如图,点D在边BC上,DE⊥AB,DF⊥BC,垂足分别为点E,D,BD=CF,BE=CD.若∠AFD=155°,则∠EDF= . 16. 已知AB=4,AC=2,D是BC的中点, AD是整数,则AD= .
16. 已知AB=4,AC=2,D是BC的中点, AD是整数,则AD= .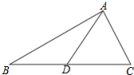 17. 如图所示,AB=AC , AD=AE , ∠BAC=∠DAE , ∠1=25°,∠2=30°,则∠3= .
17. 如图所示,AB=AC , AD=AE , ∠BAC=∠DAE , ∠1=25°,∠2=30°,则∠3= .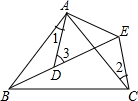 18. 如图,△ABC中,AB=AC,点D是△ABC内部一点,DB=DC,点E是边AB上一点,若CD平分∠ACE,∠AEC=100°,则∠BDC=°.
18. 如图,△ABC中,AB=AC,点D是△ABC内部一点,DB=DC,点E是边AB上一点,若CD平分∠ACE,∠AEC=100°,则∠BDC=°.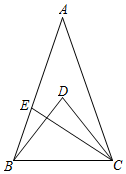 19. 如图,△ABC和△CDE都是等边三角形,AD和BE相交于点F.点B,C,D三点在同一直线上,则AD和BE的大小关系是 , 它们所成的锐角∠AFB= .
19. 如图,△ABC和△CDE都是等边三角形,AD和BE相交于点F.点B,C,D三点在同一直线上,则AD和BE的大小关系是 , 它们所成的锐角∠AFB= .
三、解答题
-
20. 如图,已知△ABC≌△DEF,且∠A=75°,∠B=35°,ED=10cm,求∠F的度数与AB的长.
 21. 如图,已知点A、E、F、C在同一直线上,∠A=∠C,AE=CF,AD=CB,求证:BE//DF
21. 如图,已知点A、E、F、C在同一直线上,∠A=∠C,AE=CF,AD=CB,求证:BE//DF 22. 已知:如图,在△ABC中,AD平分∠BAC,且BD=CD.求证:∠B=∠C.
22. 已知:如图,在△ABC中,AD平分∠BAC,且BD=CD.求证:∠B=∠C. 23. 尺规作图(需保留作图痕迹)
23. 尺规作图(需保留作图痕迹)
 (1)、已知△ABC,将△ABC沿直线AD折叠,使得边AC落在边AB上,作折痕AD.(2)、已知∠MON,点A在其内部,在ON上作一点P,使得点P到点A的距离与点P到射线OM的距离之和最短.24. 如图,AD是△ABC中∠BAC的平分线,DE⊥AB于点E,S△ABC=7,DE=2,AB=4,求AC的长.
(1)、已知△ABC,将△ABC沿直线AD折叠,使得边AC落在边AB上,作折痕AD.(2)、已知∠MON,点A在其内部,在ON上作一点P,使得点P到点A的距离与点P到射线OM的距离之和最短.24. 如图,AD是△ABC中∠BAC的平分线,DE⊥AB于点E,S△ABC=7,DE=2,AB=4,求AC的长. 25. 在△ABC中,AB=AC,D是直线BC上一点,以AD为一条边在AD的右侧作△ADE,使AE=AD,∠DAE=∠BAC,连接CE.
25. 在△ABC中,AB=AC,D是直线BC上一点,以AD为一条边在AD的右侧作△ADE,使AE=AD,∠DAE=∠BAC,连接CE. (1)、如图,当点D在BC延长线上移动时,若∠BAC=25°,则∠DCE=;(2)、设∠BAC=α,∠DCE=β.
(1)、如图,当点D在BC延长线上移动时,若∠BAC=25°,则∠DCE=;(2)、设∠BAC=α,∠DCE=β.①当点D在BC延长线上移动时,α与β之间有什么数量关系?请说明理由;
②当点D在直线BC上(不与B、C两点重合)移动时,α与β之间有什么数量关系?请直接写出你的结论.
26. (1)、【初步探索】
(1)、【初步探索】
如图1:在四边形中, , , 、分别是、上的点,且 , 探究图中、、之间的数量关系.小明同学探究此问题的方法是:延长到点 , 使 . 连接 , 先证明 , 再证明 , 可得出结论,他的结论应是;
(2)、【灵活运用】
如图2,若在四边形中, , , 、分别是、上的点,且 , 上述结论是否仍然成立,并说明理由;(3)、【拓展延伸】
如图3,已知在四边形中, , , 若点在的延长线上,点在的延长线上,如图3所示,仍然满足 , 请写出与的数量关系,给出证明过程.