江苏省扬州市江都区邵樊片2021-2022学年八年级上学期第一次质量检测数学试题
试卷更新日期:2022-09-01 类型:月考试卷
一、单选题
-
1. 下列图形是几家电信公司的标志,其中是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、
-
2. 如图所示,点F,A,D,C在同一直线上,△ABC≌△DEF,AD=3,CF=10,则AC等于( )
 A、5 B、6 C、6.5 D、7
A、5 B、6 C、6.5 D、7 -
3. 下列图形中对称轴条数最多的是( )A、等边三角形 B、正方形 C、等腰三角形 D、等腰梯形
-
4. 如图,在△ABC中,BC=8cm,AB的垂直平分线交AB于点D,交边AC于点E,△BCE的周长等于18cm,则AC的长等于( )
 A、6 cm B、10 cm C、8cm D、12 cm
A、6 cm B、10 cm C、8cm D、12 cm -
5. 在三角形内部,且到三角形三边距离相等的点是( )A、三角形三条中线的交点 B、三角形三条高线的交点 C、三角形三条角平分线的交点 D、三角形三边垂直平分线的交点
-
6. 如图,P是∠BAC的平分线AD上的一点,PE⊥AC于点E,已知PE=3,则点P到AB的距离是( )
 A、3 B、4 C、5 D、无法确定
A、3 B、4 C、5 D、无法确定 -
7. 在下列说法中,正确的有( )
①三角分别相等的两个三角形全等;②三边分别相等的两个三角形全等;③两角及其中一组等角的对边分别相等的两个三角形全等;④两边及其中一组等边的对角分别相等的两个三角形全等.
A、1个 B、2个 C、3个 D、4个 -
8. 如图,点A,E,F,D在同一直线上,若AB∥CD,AB=CD,AE=FD,则图中的全等三角形有 ( )
 A、1对 B、2对 C、3对 D、4对
A、1对 B、2对 C、3对 D、4对
二、填空题
-
9. 如果△ABC与△关于直线对称,且∠A=50°, , 那么=
-
10. 如图,沿直线AD折叠,与重合,若 , 则度.

-
11. 如图所示,AB=AC , AD=AE , ∠BAC=∠DAE , ∠1=25°,∠2=30°,则∠3= .
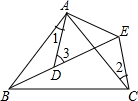
-
12. 小明从镜子中看到对面电子钟如图所示,这时的时刻应是.

-
13. 如图,已知B、E、F、C在同一直线上,BE=CF,AF=DE,则添加条件 , 可以判断△ABF≌△DCE.
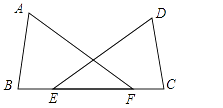
-
14. 如图是4×4正方形网络,其中已有3个小方格涂成了黑色.现在要从其余13个白色小方格中选出一个也涂成黑色的图形成为轴对称图形,这样的白色小方格有个.

-
15. 如图,AB垂直平分CD,AC=6,BD=4,则四边形ADBC的周长是 .

-
16. 如图为6个边长相等的正方形的组合图形,则∠1+∠2+∠3=.

-
17. 如图, 是 的角平分线, 于 , 的面积是 ,则 .
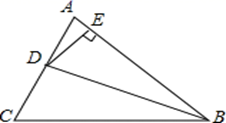
-
18. 如图,点是内任意一点, , , 点和点分别是射线和射线上的动点,则周长的最小值为 .

三、解答题
-
19. 作图题:如图,已知和、两点,在内部找一点 , 使 , 且到的两边、的距离相等.

-
20. 如图,在长度为1个单位长度的小正方形组成的正方形网格中,点、、在小正方形的顶点上.

⑴在图中画出与关于直线成轴对称的;
⑵线段被直线▲ ;
⑶的面积为 ▲ ;
⑷在直线上找一点 , 使的长最短.
-
21. 已知AF=ED,AE=FD,点B、C在AD上,AB=CD,
 (1)、图中共有对全等三角形.(2)、我会说明△▲ ≌△▲ . (写出证明过程)
(1)、图中共有对全等三角形.(2)、我会说明△▲ ≌△▲ . (写出证明过程) -
22.
如图,点B、E、C、F在同一条直线上,∠A=∠D,∠B=∠DEF,BE=CF.求证:AC=DF.

-
23. 如图,△ABC中,∠BAC=110°,DE,FG分别为AB,AC的垂直平分线,E,G分别为垂足.
 (1)、求∠DAF的度数;(2)、如果BC=10cm,求△DAF的周长.
(1)、求∠DAF的度数;(2)、如果BC=10cm,求△DAF的周长. -
24. 如图,在 中,D是 边的中点, 于点E , 于点F , 且 .
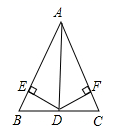
求证: 平分 .
-
25. 如图,在中,平分 , , 于点 , 点在上, .
 (1)、求证: .(2)、若 , , 求的长.
(1)、求证: .(2)、若 , , 求的长. -
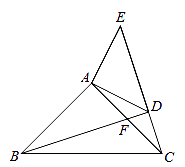
26. 如图,已知:在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD.图中的CE、BD有怎样的大小和位置关系?试证明你的结论.
-
27. 如图,已知在△ABC中,AB=AC,∠BAC=90°,分别过B、C向过A的直线作垂线,垂足分别为E、F.
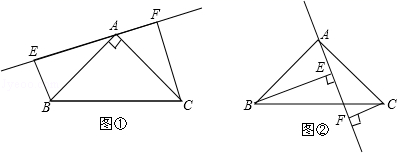 (1)、如图①过A的直线与斜边BC不相交时,求证:EF=BE+CF;(2)、如图②过A的直线与斜边BC相交时,其他条件不变,若BE=10,CF=3,求:FE长.
(1)、如图①过A的直线与斜边BC不相交时,求证:EF=BE+CF;(2)、如图②过A的直线与斜边BC相交时,其他条件不变,若BE=10,CF=3,求:FE长. -
28. 如图,已知中, , , , 点为的中点.
 (1)、如果点在线段上以的速度由点向点运动,同时,点在线段上由点向点运动.
(1)、如果点在线段上以的速度由点向点运动,同时,点在线段上由点向点运动.①若点的运动速度与点的运动速度相等,经过1秒后,与是否全等,请说明理由;
②若点的运动速度与点的运动速度不相等,当点的运动速度为多少时,能够使与全等?
(2)、若点以②中的运动速度从点出发,点以原来的运动速度从点同时出发,都逆时针沿三边运动,则经过秒后,点与点第一次在的边上相遇?(在横线上直接写出答案,不必书写解题过程)
