江苏省盐城市盐都区第一共同体2021-2022学年八年级上学期第一次月考数学试卷
试卷更新日期：2022-09-01 类型：月考试卷
一、单选题
-
1. 下列图形是几家电信公司的标志，其中是轴对称图形的是（ ）A、
B、
C、
D、
2. 已知△ABC≌△DEF，∠A=80°，∠E=40°，则∠F等于（ ）A、80° B、40° C、60° D、120°3. 如图 ， ， 下列条件中不能判定的是（ ）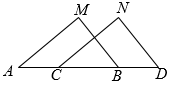
A、 B、 C、 D、4. 如图，△ABC≌△ADE，∠B＝25°，∠E＝105°，∠EAB＝10°，则∠BAD为（ ）
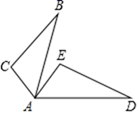A、50° B、60° C、80° D、120°5. 如图，已知太阳光线AC和DE是平行的，在同一时刻两根高度相同的木杆竖直插在地面上，在太阳光照射下，其影子一样长．这里判断影长相等利用了全等图形的性质，其中判断△ABC≌△DFE的依据是（ ）
A、SAS B、AAS C、HL D、ASA6. 在联欢晚会上，有A、B、C三名同学站在一个三角形的三个顶点位置上，他们在玩抢凳子游戏，要求在他们中间放一个木凳，谁先抢到凳子谁获胜，为使游戏公平，则凳子应放的最适当的位置在△ABC的（ ）A、三边中线的交点 B、三条角平分线的交点 C、三边上高的交点 D、三边中垂线的交点7. 如图，已知CD⊥AB于点D，BE⊥AC于点E，CD、BE交于点O，且AO平分∠BAC，则图中的全等三角形共有（ ）对
A、2 B、3 C、4 D、58. 如图，BD是ABC的外角∠ABP的角平分线，DA＝DC，DE⊥BP于点E，若AB＝5，BC＝3，则BE的长为（ ）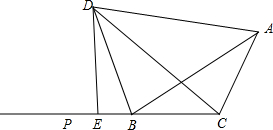
A、2 B、1.5 C、1 D、0二、填空题
-
9. 如图，图中显示的是从镜子中看到背后墙上的电子钟读数，由此你可以推断这时的实际时间是.
10. 如图，已知B、E、F、C在同一直线上，BE=CF，AF=DE，则添加条件 ， 可以判断△ABF≌△DCE．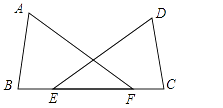
11.如图，某同学一不小心将三角形玻璃打碎，现要带③到玻璃店配一块完全相同的玻璃，这样做的依据是
12. 如图，ABC中，AB+AC＝4，BC的垂直平分线l交AC于D，则ABD的周长为 ．
13. 如图，在网格中与ABC成轴对称的格点三角形一共有 个．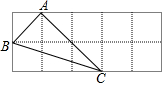
14. 如图，AD是△ABC中∠BAC的角平分线，DE⊥AB于点E，DF⊥AC于点F，S△ABC=7，DE=2，AB=4，则AC长是 ．
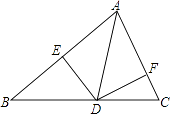15. 如图，在△ABC中，∠ACB＝90°，AC＝7cm，BC＝3cm，CD为AB边上的高．点E从点B出发在直线BC上以2cm/s的速度移动，过点E作BC的垂线交直线CD于点F.当点E运动s时，CF＝AB．
16. 如图，将△ABC沿着过BC的中点D的直线折叠，使点B落在边AC上的点B1处，称为第一次操作，折痕DE到AC的距离为h1；还原纸片后，再将△BDE沿着过BD的中点D1的直线折叠，使点B落在DE边上的点B2处，称为第二次操作，折痕D1E1到AC的距离记为h2；按上述方法不断操作下去，经过第n次操作后得到的折痕Dn﹣1En﹣1到AC的距离记为hn ， 如h1＝1，则hn的值为 ．
三、解答题
-
17. 作图：(1)、如图1，ABC在边长为1的正方形网格中：
①画出ABC关于直线l轴对称的DEF（其中D、E、F是A、B、C的对应点）；
②在直线l上画一点Q，使得AQ+CQ的值最小．
③的面积为 ▲ ．
(2)、如图2，在四边形ABCD内找一点P，使得点P到AB、AD的距离相等，并且点P到点B、C的距离也相等．（用直尺与圆规作图，不写作法，保留作图痕迹）．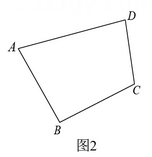
18. 如图，点D在AB上，点E在AC上，AB=AC，AD=AE，试说明∠B=∠C．
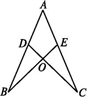19. 如图，已知点 B、F、C、E 在一条直线上，BF = CE，AC = DF，且 AC∥DF． 求证：∠B =∠E.
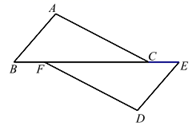20. 如图，AC⊥BC，DC⊥EC，AC=BC，DC=EC，则AE、BD有什么关系？请证明你的结论.
21. 如图，AB=AD，CB⊥AB，CD⊥AD，E、F分别是BC、DC的中点．求证：AE=AF.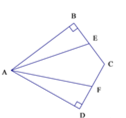
22. 如图，△ABC中，AD⊥BC，EF垂直平分AC，交AC于点F，交BC于点E，且BD=DE．
(1)、若∠BAE=40°，求∠C的度数；(2)、若△ABC周长13cm，AC=6cm，求DC长．23. 如图，AD平分∠BAC，∠BAC+∠ACD=180°，E在AD上，BE的延长线交CD于F，连CE，且∠1=∠2，试说明AB=AC．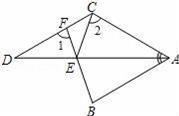
24. 如图，ABC的边BC的垂直平分线DE交ABC的外角平分线AD于点D，DF⊥AB于点F，且AB＞AC，试探究BF、AC、AF之间的数量关系，并说明理由．
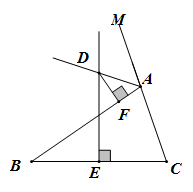25. 已知点C是∠MAN平分线上一点，∠BCD的两边CB、CD分别与射线AM、AN相交于B，D两点，且∠ABC+∠ADC＝180°.过点C作CE⊥AB，垂足为E.
(1)、如图1，当点E在线段AB上时，求证：BC＝DC；(2)、如图2，当点E在线段AB的延长线上时，探究线段AB、AD与BE之间的等量关系；(3)、如图3，在（2）的条件下，若∠MAN＝60°，连接BD，作∠ABD的平分线BF交AD于点F，交AC于点O，连接DO并延长交AB于点G.若BG＝1，DF＝2，求线段DB的长.