江苏省盐城市东台市四联盟2021-2022学年八年级上学期第一次阶段测试数学试卷

试卷更新日期：2022-09-01 类型：月考试卷

进入出卷网下载

一、单选题

1. 下列图形标志中，不是轴对称图形的（　　）

A、 B、 C、 D、

查看试题解析
2. 下列说法正确的是（）

A、形状相同的两个三角形一定全等 B、面积相等的两个三角形一定全等 C、所有的正方形都全等 D、一个图形经过平移后，前后两个图形一定全等

查看试题解析
3. 如图，要测量河两岸相对的两点A，B的距离，先在 $A B$ 的垂线 $B F$ 上取两点C，D，使 $B C = C D$ ，再作出 $B F$ 的垂线 $D E$ ，使点A，C，E在同一条直线上，可以说明 $△ A B C ≌ △ E D C$ ，得 $A B = D E$ ，因此测得 $D E$ 的长就是 $A B$ 的长，判定 $△ A B C ≌ △ E D C$ ，最恰当的理由是（）

A、 $S A S$ B、 $H L$ C、 $S S S$ D、 $A S A$

查看试题解析
4. 如图， $Δ A B C ≅ Δ A D E$ ，若 $∠ B = 40 °$ ， $∠ E = 30 °$ ，则 $∠ D A E$ 的度数为（）

A、 $70 °$ B、 $110 °$ C、 $120 °$ D、 $130 °$

查看试题解析
5. 如图，若 $△ A B C$ ≌ $△ D E F$ ， $BC = 7.5$ ， $CF = 5$ ，则CE的长为（）

A、1.5 B、2 C、2.5 D、3.5

查看试题解析
6. 如图，在 $△ A B C$ 中， $D$ 为 $B C$ 的中点，若 $A C = 3 ， A D = 4$ .则 $A B$ 的长不可能是（）

A、5 B、7 C、8 D、9

查看试题解析
7. 如图，在 $△ A B C$ 中， $∠ C = 90 °$ ， D是 $A C$ 上一点， $D E ⊥ A B$ 于点E， $B E = B C$ ，连接 $B D$ ，若 $A C = 8 cm$ ，则 $A D + D E$ 等于（）

A、 $6cm$ B、 $7cm$ C、 $8cm$ D、 $10cm$

查看试题解析
8. 如图，已知△ABC中，AB=AC=24cm，∠B=∠C ， BC=16cm，点D为AB的中点，如果点P在线段BC上以4cm/s的速度由B点向C点运动，同时，点Q在线段CA上由C点向A点运动，当点Q的运动速度为（）cm/s时，能够在某一时刻使△BPD与△CQP全等．

A、4 B、3 C、4或3 D、4或6

查看试题解析

二、填空题

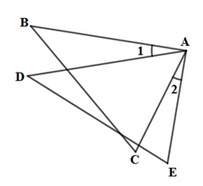
9. 如图所示，AB=AD，∠1=∠2，添加一个适当的条件，使△ABC≌△ADE，则需要添加的条件是.

查看试题解析
10. 如图，图中的两个三角形全等，图中的字母表示三角形的边长，则 $∠ 1$ 的度数等于．

查看试题解析
11. 如图为6个边长相等的正方形的组合图形，则∠1+∠2+∠3＝.

查看试题解析
12. 如图，点 $B$ 、 $E$ 、 $C$ 、 $F$ 在同一条直线上， $A B / / D E$ ， $A B = D E$ ， $∠ A = ∠ D$ ， $B F = 10$ ， $B C = 6$ ，则 $E C =$ .

查看试题解析
13. 如图，在△ABC中，∠C=50°，按图中虚线将∠C剪去后，∠1+∠2等于．

查看试题解析
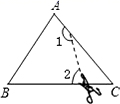14. 如图，将一张矩形纸片ABCD沿EF折叠，使顶点C，D分别落在点C′，D′处，C′E交AF于点G，若∠CEF=70°，则∠GFD′=°．

查看试题解析
15. 如图， $A E ⊥ A B$ ，且 $A E = A B$ ， $B C ⊥ C D$ ，且 $B C = C D$ ，请按照图中所标注的数据计算图中实线所围成的图形的面积 $S =$ .

查看试题解析
16. 如图，在 $△ O A B$ 和 $△ O C D$ 中， $O A = O B$ ， $O C = O D$ ， $O A > O C$ ， $∠ A O B = ∠ C O D = 30 °$ 连接AC，BD交于点M，连接OM，下列结论：① $A C = B D$ ；② $∠ C M D = 30 °$ ；③ $O M$ 平分 $∠ C O B$ ；④ $∠ M O A = ∠ M B A$ .正确的结论序号是．

查看试题解析

三、解答题

17. 下面是“作一个角等于已知角”的尺规作图过程．已知：∠AOB，求作：一个角，使它等于∠AOB．作法：如图

①作射线 $O^{'} A^{'}$ ；

②以O为圆心，任意长为半径作弧，交OA于C，交OB于D；

③以 $O^{'}$ 为圆心，OC为半径作弧 $C^{'} E^{'}$ ，交 $O A^{'}$ 于 $C^{'}$ ；

④以 $C^{'}$ 为圆心，CD为半径作弧，交弧 $C^{'} E^{'}$ 于 $D^{'}$ ；

⑤过点 $D^{'}$ 作射线 $O^{'} B^{'}$ ，则 $∠ A^{'} O^{'} B^{'}$ 就是所求作的角

请完成下列问题：

(1)、该作图的依据是（填序号）
①ASA；②SAS；③AAS；④SSS

(2)、请证明 $∠ A^{'} O^{'} B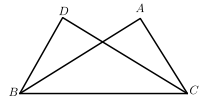^{'}$ ＝∠AOB

查看试题解析
18. 已知， $∠ A B C = ∠ D C B$ ， $∠ A C B = ∠ D B C$ ，求证： $△ A B C ≌ △ D C B$ ．

查看试题解析
19. 如图，在四边形ABCD中，AB∥CD，连接BD，点E在BD上，连接CE，若∠1＝∠2，AB＝ED，求证：DB＝CD.

查看试题解析
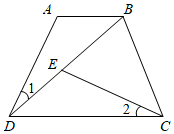20. 如图，DE⊥AB，CF⊥AB，垂足分别是点E、F，DE=CF，AE=BF，求证：AC∥BD．

查看试题解析
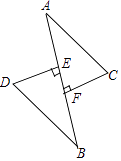21. 如图，在长度为1个单位长度的小正方形组成的正方形网格中，点A、B、C在小正方形的顶点上．

⑴在图中画出与 $△ A B C$ 关于直线l₁成轴对称的 $△ A_{1} B_{1} C_{1}$ ；

⑵在图中画出与 $△ A B C$ 关于直线l₂成轴对称的 $△ A_{2} B_{2} C_{2}$ ；

⑶求 $△ A B C$ 的面积．（请用2B铅笔作图）

查看试题解析
22. 如图，在△ABC中，∠BAC＝90°，AB＝AC，直线m经过点A，BD⊥直线m，CE⊥直线m，垂足分别为D，E．

(1)、求证：△ABD≌△ACE；

(2)、若BD＝2cm，CE＝4cm，求DE的长．

查看试题解析
23. 如图，A、B、C、D是四个村庄，B、D、C三村在一条东西走向公路的沿线上，且D村到B村、C村的距离相等；村庄A、C，A、D间也有公路相连，且公路AD是南北走向；只有村庄A、B之间由于间隔了一个小湖，所以无直接相连的公路．现决定在湖面上造一座斜拉桥，测得AC＝3千米，AE＝1.2千米，BF＝0.7千米．试求建造的斜拉桥至少有多少千米？

查看试题解析
24. 如图，点E、F分别为线段AC上的两个点，且DE⊥AC于点E，BF⊥AC于点F，若AB＝CD，AE＝CF，BD交AC于点M.求证：

(1)、AB∥CD；

(2)、点M是线段EF的中点.

查看试题解析
25. 如图1，AD为△ABC的中线，延长AD至E，使DE＝AD．

(1)、试证明：△ACD≌△EBD；

(2)、用上述方法解答下列问题：如图2，AD为△ABC的中线，BM交AD于G，交AC于M，若AM＝GM，求证：BG＝AC．

查看试题解析
26. 在△ABC中，AB=AC，点D是直线BC上一点（不与B、C重合），以AD为一边在AD的右侧作△ADE，使AD=AE，∠DAE =∠BAC，连接CE．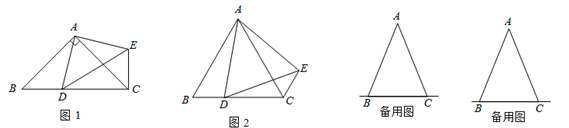

(1)、如图1，当点D在线段BC上，如果∠BAC=90°，则∠BCE=度；

(2)、设 $∠ B A C = α$ ， $∠ B C E = β$ ．
①如图2，当点在线段BC上移动，则 $α$ ， $β$ 之间有怎样的数量关系？请说明理由；

②当点在直线BC上移动，则 $α$ ， $β$ 之间有怎样的数量关系？请直接写出你的结论．

查看试题解析