江苏省盐城市东台市第五联盟2021-2022学年八年级上学期10月月考数学试卷

试卷更新日期：2022-09-01 类型：月考试卷

进入出卷网下载

一、单选题

1. 在下列“禁毒”、“和平”、“志愿者”、“节水”这四个标志中，属于轴对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
2. 如图，工人师傅在安装木制门框时，为防止变形常常钉上两根木条，这样做的依据是（）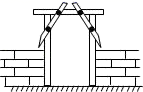

A、三角形具有稳定性 B、两点之间，线段最短 C、直角三角形的两个锐角互为余角 D、垂线段最短

查看试题解析
3. 已知△ABC≌△DEF，∠A=80°，∠E=40°，则∠F等于（）

A、80° B、40° C、60° D、120°

查看试题解析
4. 如图为了测量B点到河对面的目标A之间的距离，在B点同侧选择了一点C，测得∠ABC＝65°，∠ACB＝35°，然后在M处立了标杆，使∠MBC＝65°，∠MCB＝35°，得到△MBC≌△ABC，所以测得MB的长就是A，B两点间的距离，这里判定△MBC≌△ABC的理由是（）

A、SAS B、AAA C、SSS D、ASA

查看试题解析
5. 如图，已知OA＝OB，OC＝OD，AD和BC相交于点E，则图中共有全等三角形的对数（　　）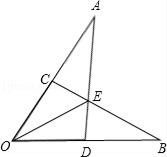

A、2对 B、3对 C、4对 D、5对

查看试题解析
6.
小明不慎将一块三角形的玻璃摔碎成如图所示的四块（即图中标有1、2、3、4的四块），你认为将其中的哪一些块带去，就能配一块与原来一样大小的三角形？应该带（　　）

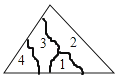A、第1块 B、第2块 C、第3块 D、第4块

查看试题解析
7. 如图是用直尺和圆规作一个角等于已知角的示意图，说明 $∠ O^{'} = ∠ O$ 的依据是（）

A、 $S A S$ B、 $S S S$ C、 $A A S$ D、 $A S A$

查看试题解析
8. 如图，在 $3 \times 3$ 的正方形网格中两个小正方形被涂黑，再将图中其余小正方形任意一个涂黑，使得整个图形（包括网格）构成一个轴对称图形，那么涂法共有（）

A、4种 B、5种 C、6种 D、7种

查看试题解析

二、填空题

9. 已知△ABC≌△DEF ，△DEF 的周长为32cm ，DE = 9cm ，EF = 12cm ，则 AC =cm .

查看试题解析
10. 如图，桌面上有M、N两球，若要将M球射向桌面的任意一边，使一次反弹后击中N球，则4个点中，可以瞄准的是点.

查看试题解析
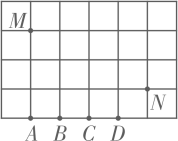11. 如图，△ABO≌△CBO，若∠A=85°，∠ABO=35°，则∠BOC的度数为°．

查看试题解析
12. 黑板上写着在正对着黑板的镜子里的像是.

查看试题解析
13. 在如图所示的2×2方格中，连接AB、AC，则∠1+∠2=度.

查看试题解析
14. 如图，点B在AE上，∠C=∠D，要能证△ABC≌△ABD，只需再补充一个条件：（写一个即可）．

查看试题解析
15. 如图，CA⊥BC，垂足为C，AC=2cm，BC=6cm，射线BM⊥BQ，垂足为B，动点P从C点出发以1cm/s的速度沿射线CQ运动，点N为射线BM上一动点，满足PN=AB，随着P点运动而运动，当点P运动秒时，△BCA与点P、N、B为顶点的三角形全等.

查看试题解析
16. 如图，已知四边形 $A B C D$ 中， $A B = 10$ 厘米， $B C = 8$ 厘米， $C D = 12$ 厘米， $∠ B = ∠ C$ ，点 $E$ 为 $A B$ 的中点．如果点P在线段BC上以3厘米/秒的速度由B点向C点运动，同时，点Q在线段CD上由C点向D点运动．当点 $Q$ 的运动速度为厘米/秒时，能够使 $△ B E P$ 与 $△ C P Q$ 全等．

查看试题解析

三、解答题

17. 如图，AD、BC交于点O ， AC＝BD ， BC＝AD ．求证：∠C＝∠D ．

查看试题解析
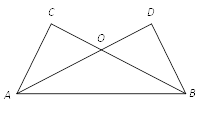18. 如图，AD＝BC，AB⊥CA，CD⊥CA．求证：∠B＝∠D．

查看试题解析
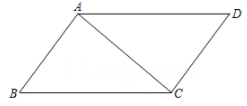19. 如图，点A、D、B、E在一条直线上，AD=BE，∠C=∠F，BC∥EF.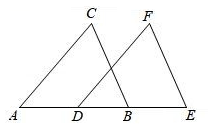

求证：

(1)、△ABC≌△DEF；

(2)、AC∥DF

查看试题解析
20. 如图，方格纸中每个小方格都是边长为1个单位的正方形，已知 $△ A B C$ 的三个顶点在格点上．

⑴画出 $△ A_{1} B_{1} C_{1}$ ，使它与 $△ A B C$ 关于直线a对称；

⑵求出 $△ A_{1} B_{1} C_{1}$ 的面积；

⑶在直线a上画出点P，使 $P A + P C$ 最小

查看试题解析
21. 杨阳同学沿一段笔直的人行道行走，在由A步行到达B处的过程中，通过隔离带的空隙O，刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语，其具体信息汇集如下：
如图，AB∥OH∥CD，相邻两平行线间的距离相等，AC，BD相交于O，OD⊥CD．垂足为D，已知AB=20米，请根据上述信息求标语CD的长度．

查看试题解析
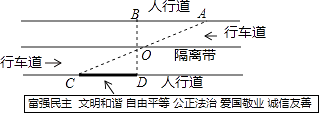22. 已知：如图，点E、A、C在同一条直线上，AB∥CD，AB=CE，∠B=∠E．

(1)、求证：△ABC≌△CED；

(2)、若∠B=25°，∠ACB=45°，求∠ADE的度数．

查看试题解析
23. 如图：在△ABC中，BE、CF分别是AC、AB两边上的高，在BE上截取BD=AC，在CF的延长线上截取CG=AB，连接AD、AG．

(1)、求证：AD=AG；

(2)、AD与AG的位置关系如何，请说明理由．

查看试题解析
24. 综合与实践

(1)、观察理解：如图1， $△ A B C$ 中， $∠ A C B = 90 °$ ， $A C = B C$ ，直线 $l$ 过点 $C$ ，点 $A$ 、 $B$ 在直线 $l$ 同侧， $B D ⊥ l$ ， $A E ⊥ l$ ，垂足分别为 $D$ 、 $E$ ，由此可得： $∠ A E C = ∠ C D B = 90 °$ ，所以 $∠ C A E + ∠ A C E = 90 °$ ，又因为 $∠ A C B = 90 °$ ，所以 $∠ B C D + ∠ A C E = 90 °$ ；所以 $∠ C A E = ∠ B C D$ ，又因为 $A C = B C$ ，所以 $△ A E C ≅ △ C D B$ （）；（请填写全等判定的方法）

(2)、理解应用：如图2， $A E ⊥ A B$ 且 $A E = A B$ ， $B C ⊥ C D$ 且 $B C = C D$ ，利用（1）中结论，请按照图中所标注的数据计算图中实线所围成的图形的面积 $S =$ ；

(3)、类比探究：如图3， $Rt △ A B C$ 中， $∠ A C B = 90 °$ ， $A C = 4$ ，将斜边AB绕点A逆时针旋转90°至 $A B^{'}$ ，连接 $B^{'} C$ ，求 $△ A B^{'} C$ 的面积

(4)、拓展提升：如图4，点B，C在 $∠ M A N$ 的边AM，AN上，点E、F在∠MAN内部的射线AD上，∠1、∠2分别是 $△ A B E$ 、 $△ C A F$ 的外角，已知 $A B = A C$ ， $∠ 1 = ∠ 2 = ∠ B A C$ ，求证： $C F + E F = B E$

(5)、拓展应用：如图5，在 $△ A B C$ 中， $A B = A C$ ， $A B > B C$ ，点D在边BC上， $C D = 2 B D$ ，点E、F在线段AD上， $∠ 1 = ∠ 2 = ∠ B A C$ ，若 $△ A B C$ 的面积为15，则 $△ A C F$ 与 $△ B D E$ 的面积之和为．

查看试题解析