江苏省苏州市高新区2021-2022年八年级上学期数学自主检测试卷
试卷更新日期：2022-09-01 类型：月考试卷
一、单选题
-
1. 下列倡导节约的图案中，是轴对称图形的是（ ）A、
B、
C、
D、
2.如图，桌面上有M、N两球，若要将M球射向桌面的任意一边，使一次反弹后击中N球，则4个点中，可以瞄准的是（ ）
A、点A B、点B C、点C D、点D3. 等腰三角形的顶角等于80°，则它的底角是（ ）A、80° B、50° C、40° D、80°或50°4. 到三角形三条边距离相等的点是此三角形（ ）A、三条角平分线的交点 B、三条中线的交点 C、三条高的交点 D、三边中垂线的交点5. 如图，在△ABC中，AC=AD=BD，∠B=35°，则∠CAD的度数为（ ）
A、70° B、55° C、40° D、35°6. 已知ABC中，a、b、c分别是∠A、∠B、∠C的对边，下列条件不能判断ABC是直角三角形的是（ ）A、∠A-∠B＝∠C B、∠A∶∠B∶∠C＝3∶4∶5 C、（b＋c）（b-c）＝a2 D、a＝7，b＝24，c＝257. 如图，△ABC 中，AB=AC，AD 是∠BAC 的平分线，已知 AB=5，AD=3，则 BC的长为（ ）
A、5 B、4 C、10 D、88. 在 中， ， 于 ， 平分 交 于 ，则下列结论一定成立的是（ ）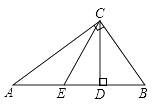
A、 B、 C、 D、9. 将一正方形纸片按下列顺序折叠，然后将最后折叠的纸片沿虚线剪去上方的小三角形，将纸片展开，得到的图形是（ ）.
A、
B、
C、
D、
10. 如图，在RtΔABC中，∠ACB＝90°，AC=9，BC=12，AD是∠BAC的平分线，若点P，Q分别是AD和AC上的动点，则PC＋PQ的最小值是（ ）
A、 B、 C、12 D、15二、填空题
-
11. 在“线段、圆、等边三角形、正方形、角”这五个图形中，对称轴最多的图形是 ．12. 已知等腰三角形的两边长为3和6，则它的周长为.13. 直角三角形的斜边为5cm，两直角边之比为3∶4，那么这个直角三角形的周长为 ．14. 如图是4×4正方形网络，其中已有3个小方格涂成了黑色.现在要从其余13个白色小方格中选出一个也涂成黑色的图形成为轴对称图形，这样的白色小方格有个.
15. 如图，在△ABC中，AB=AC=5，BC=6，点M为BC中点，MN⊥AC于点N，则MN的长为 ．
16. 如图，任意画一个∠BAC=60°的△ABC，再分别作△ABC的两条角平分线BE和CD，BE和CD相交于点P，连接AP，有以下结论：①∠BPC=120°；②AP平分∠BAC；③AD=AE；④PD=PE；⑤BD+CE=BC；其中正确的结论为 ． （填写序号）
17. 如图，∠MON=90°，已知△ABC中，AC=BC=13，AB=10，△ABC的顶点A、B分别在射线OM、ON上，当点B在ON上运动时，A随之在OM上运动，△ABC的形状始终保持不变，在运动的过程中，点C到点O的最小距离为 ．
三、解答题
-
18. 如图，∠ADB=∠ABC=90°，∠DAB=∠BAC，BD=6，P为AC上一点，则BP的最小值为
19. 如图，在11×11的正方形网格中，网格中有一个格点△ABC（即三角形的顶点都在格点上）．
⑴在图中作出△ABC关于直线l对称的△A1B1C1（要求A与A1 ， B与B1 ， C与C1相对应）；
⑵在直线l上找一点P，使得PA=PB．
20. 如图，在7×7网格中，每个小正方形的边长都为1.
(1)、△ABC的面积为；(2)、判断△ABC的形状，并说明理由.21. 如图，红星村A和幸福村B在一条小河的同侧，它们到河岸的距离 ， 分别为1和3 ， 又知道的长为3 ， 现要在河岸上建一水厂向两村输送自来水，铺设水管的工程费用为每千米20000元．
(1)、请在上选择水厂位置，使铺设水管的费用最省（作图工具不限，保留作图痕迹）；(2)、求铺设水管的最省总费用．22. 如图，在△ABC中，AB＝AC ， AB的垂直平分线MN交AC于点D ， 交AB于点E ．
(1)、若∠A＝40°，求∠DBC的度数；(2)、若AE＝6，△CBD的周长为20，求△ABC的周长．23. 如图，已知CD=3cm，AD=4cm，∠ADC=90°，BC=12cm，AB=13cm，求阴影部分的面积.
24. 已知，如图，△ABC和△ECD都是等腰直角三角形，∠ACB=∠DCE=90°，D为AB边上一点．
(1)、求证：BD=AE．(2)、若线段AD=5，AB=17，求线段ED的长．25. 如图，△ABC中，BE⊥AC，CF⊥AB，垂足分别为E、F，M为BC的中点．
(1)、求证：ME=MF；(2)、若∠A=40°，求∠FME的度数．26. 如图，AO是边长为2的等边ABC的高，点D是线段AO上的一个动点（点D不与点A、O重合），以CD为一边在AC下方作等边CDE，连结BE并延长，交AC的延长线于点F．
(1)、求证：；(2)、当CEF为等腰三角形时：①求∠ACD的度数；②求CEF的面积．27. 如图1，△ABC中，CD⊥AB于D，且BD：AD：CD＝2：3：4；
(1)、试说明△ABC是等腰三角形；(2)、已知S△ABC＝40cm2 ， 如图2，动点M从点B出发以每秒1cm的速度沿线段BA向点A运动，同时动点N从点A出发以相同速度沿线段AC向点C运动，当其中一点到达终点时整个运动都停止.设点M运动的时间为t（秒）.①若△DMN的边与BC平行，求t的值；
②若点E是边AC的中点，在点M运动的过程中，△MDE能否成为等腰三角形?若能，求出t的值；若不能，请说明理由.