江苏省盐城市东台市二盟2021-2022学年八年级上学期10月月考数学试卷
试卷更新日期:2022-09-01 类型:月考试卷
一、单选题
-
1. 下列图形中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列图形:①两个点;②线段;③角;④长方形;⑤三角形,其中一定是轴对称图形的有( )A、2个 B、3 个 C、4 个 D、5 个3. 如图,正方形ABCD的边长为4cm,则图中阴影部分的面积为( )cm2
2. 下列图形:①两个点;②线段;③角;④长方形;⑤三角形,其中一定是轴对称图形的有( )A、2个 B、3 个 C、4 个 D、5 个3. 如图,正方形ABCD的边长为4cm,则图中阴影部分的面积为( )cm2 A、4 B、16 C、12 D、84. 工人常用角尺平分一个任意角,做法如下:如图,∠AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使CM=CN,过角尺顶点C作射线OC,由此作法便可得△NOC≌△MOC,其依据是( )
A、4 B、16 C、12 D、84. 工人常用角尺平分一个任意角,做法如下:如图,∠AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使CM=CN,过角尺顶点C作射线OC,由此作法便可得△NOC≌△MOC,其依据是( ) A、SSS B、SAS C、ASA D、AAS5. 在下列各组条件中,不能判定△ABC与△DE全等的是( )A、AB=DE,∠B=∠E,∠C=∠F B、AC=DF,BC=EF,∠C=∠F C、AB=DE,BC=EF,∠A=∠D D、∠A=∠D,∠C=∠F,AC=DF6. 将一正方形纸片按下列顺序折叠,然后将最后折叠的纸片沿虚线剪去上面的小直角三角形将留下的纸片展开,得到的图形是( )
A、SSS B、SAS C、ASA D、AAS5. 在下列各组条件中,不能判定△ABC与△DE全等的是( )A、AB=DE,∠B=∠E,∠C=∠F B、AC=DF,BC=EF,∠C=∠F C、AB=DE,BC=EF,∠A=∠D D、∠A=∠D,∠C=∠F,AC=DF6. 将一正方形纸片按下列顺序折叠,然后将最后折叠的纸片沿虚线剪去上面的小直角三角形将留下的纸片展开,得到的图形是( )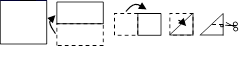 A、
A、 B、
B、 C、
C、 D、
D、 7. 如图,∠MON内有一点P,P点关于OM的轴对称点是G,P点关于ON的轴对称点是H,GH分别交OM、ON于A、B点.若GH的长为10cm,求△PAB的周长为( )
7. 如图,∠MON内有一点P,P点关于OM的轴对称点是G,P点关于ON的轴对称点是H,GH分别交OM、ON于A、B点.若GH的长为10cm,求△PAB的周长为( )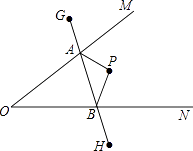 A、5cm B、10cm C、20cm D、15cm8. 如图是一个经过改造的台球桌面的示意图,图中四个角上的阴影部分分别表示四个入球孔.如果一个球按图中所示的方向被击出(球可以经过多次反射),那么该球最后将落入的球袋是( )
A、5cm B、10cm C、20cm D、15cm8. 如图是一个经过改造的台球桌面的示意图,图中四个角上的阴影部分分别表示四个入球孔.如果一个球按图中所示的方向被击出(球可以经过多次反射),那么该球最后将落入的球袋是( ) A、1号袋 B、2号袋 C、3号袋 D、4号袋
A、1号袋 B、2号袋 C、3号袋 D、4号袋二、填空题
-
9. 某同学从平面镜里看到镜子对面的电子钟的示数如图所示,这时的实际时间是 .
 10. 如图,△ABC≌△DCB,若AC=7,BE=5,则DE的长为.
10. 如图,△ABC≌△DCB,若AC=7,BE=5,则DE的长为.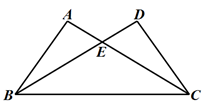 11. 如图,△ABC≌△DEF,请根据图中提供的信息,写出x= .
11. 如图,△ABC≌△DEF,请根据图中提供的信息,写出x= . 12. 如图,已知AB⊥BD , AB∥ED , AB=ED , 要证明ΔABC≌ΔEDC , 若以“SAS”为依据,还要添加的条件为;若添加条件AC=EC , 则可以用方法判定全等.
12. 如图,已知AB⊥BD , AB∥ED , AB=ED , 要证明ΔABC≌ΔEDC , 若以“SAS”为依据,还要添加的条件为;若添加条件AC=EC , 则可以用方法判定全等.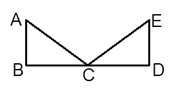 13. 如图,黄芳不小心把一块三角形的玻璃打成三块碎片,现要带其中一块去配出与原来完全一样的玻璃,正确的办法是带第块去配,其依据是定理(可以用字母简写).
13. 如图,黄芳不小心把一块三角形的玻璃打成三块碎片,现要带其中一块去配出与原来完全一样的玻璃,正确的办法是带第块去配,其依据是定理(可以用字母简写). 14. 木工师傅在做完门框后为防止变形,常像上图中所示的那样,钉上两条斜的木条,即图中的AB,CD两个木条,这是根据数学上什么原理?
14. 木工师傅在做完门框后为防止变形,常像上图中所示的那样,钉上两条斜的木条,即图中的AB,CD两个木条,这是根据数学上什么原理? 15. 如图为6个边长相等的正方形的组合图形,则∠1+∠2+∠3=.
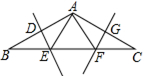
15. 如图为6个边长相等的正方形的组合图形,则∠1+∠2+∠3=. 16. 如图,AD是△ABC的角平分线,DE、DF分别是△ABD和△ACD的高,连接EF,交AD于点O.下列三个结论:①OA=OD;②AD⊥EF;③AE+DF=AF+DE.其中,一定正确的是(填序号).
16. 如图,AD是△ABC的角平分线,DE、DF分别是△ABD和△ACD的高,连接EF,交AD于点O.下列三个结论:①OA=OD;②AD⊥EF;③AE+DF=AF+DE.其中,一定正确的是(填序号).
三、解答题
-
17. 在图示的方格纸中
 (1)、作出△ABC关于MN对称的图形△A1B1C1;(2)、说明△A2B2C2是由△A1B1C1经过怎样的平移得到的?(3)、若图中每个小正方形的边长为1,则△ABC的面积是18. 如图是4×4正方形网格,其中已有3个小方格涂成了黑色.现在要从其余13个白色小方格中选出一个涂成黑色,使整个涂成黑色的图形成为轴对称图形.在下面每个网格中画出一种符合要求的图形.
(1)、作出△ABC关于MN对称的图形△A1B1C1;(2)、说明△A2B2C2是由△A1B1C1经过怎样的平移得到的?(3)、若图中每个小正方形的边长为1,则△ABC的面积是18. 如图是4×4正方形网格,其中已有3个小方格涂成了黑色.现在要从其余13个白色小方格中选出一个涂成黑色,使整个涂成黑色的图形成为轴对称图形.在下面每个网格中画出一种符合要求的图形.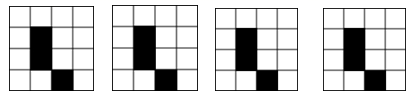 19. 如图,已知△ABC≌△DEF,点B、E、C、F在同一直线上,∠A=85°,∠B=60°,AB=8,EH=2.
19. 如图,已知△ABC≌△DEF,点B、E、C、F在同一直线上,∠A=85°,∠B=60°,AB=8,EH=2.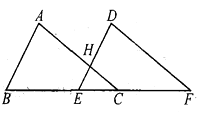 (1)、求∠F的度数与DH的长;
(1)、求∠F的度数与DH的长;
(2)、求证:AB∥DE.20. 如图,点C,F,E,B在一条直线上,∠CFD=∠BEA,CE=BF,DF=AE,写出CD与AB之间的关系,并证明你的结论.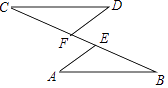 21. 如图,已知△ABC.
21. 如图,已知△ABC. (1)、用直尺和圆规按要求作图:
(1)、用直尺和圆规按要求作图:作△ABC的角平分线AD;
作∠CBE=∠ADC,BE,交CA的延长线于点E;
作AF⊥BE,垂足为F.
(2)、图中EF、BF相等吗?证明你的结论.22. 在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN,BE⊥MN,垂足分别为点D,E.求证:DE=AD+BE. 23. 如图:在△ABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连接AD、AG.
23. 如图:在△ABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连接AD、AG. (1)、求证:AD=AG;(2)、AD与AG的位置关系如何,请说明理由.
(1)、求证:AD=AG;(2)、AD与AG的位置关系如何,请说明理由.