江苏省泰州市姜堰区五校联考2021-2022学年八年级上学期10月月考数学试卷
试卷更新日期:2022-09-01 类型:月考试卷
一、单选题
-
1. 下面四个手机应用图标中是轴对称图形的是( )
A、 B、
B、 C、
C、 D、
D、 2. 下列说法:
2. 下列说法:①关于某条直线对称的两个三角形是全等三角形②两个全等的三角形关于某条直线对称③到某条直线距离相等的两个点关于这条直线对称④如果图形甲和图形乙关于某条直线对称,则图形甲是轴对称图形其中,正确说法个数是( )
A、1 B、2 C、3 D、43.如图,下列条件中,不能证明△ABC≌△DCB的是( )
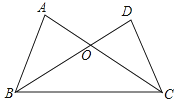 A、AB=DC,AC=DB B、AB=DC,∠ABC=∠DCB C、BO=CO,∠A=∠D D、AB=DC,∠DBC=∠ACB4. 如图所示,某同学把一块三角形的玻璃不小心打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是带哪一块去( )
A、AB=DC,AC=DB B、AB=DC,∠ABC=∠DCB C、BO=CO,∠A=∠D D、AB=DC,∠DBC=∠ACB4. 如图所示,某同学把一块三角形的玻璃不小心打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是带哪一块去( )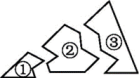 A、① B、② C、③ D、①和②5. 如图,是三个等边三角形随意摆放的图形,则∠1+∠2+∠3等于( )
A、① B、② C、③ D、①和②5. 如图,是三个等边三角形随意摆放的图形,则∠1+∠2+∠3等于( )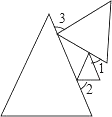 A、90° B、120° C、150° D、180°6. 如图,△ABD与△ACE均为正三角形,且AB<AC,则BE与CD之间的大小关系是( )
A、90° B、120° C、150° D、180°6. 如图,△ABD与△ACE均为正三角形,且AB<AC,则BE与CD之间的大小关系是( ) A、BE=CD B、BE>CD C、BE<CD D、大小关系不确定
A、BE=CD B、BE>CD C、BE<CD D、大小关系不确定二、填空题
-
7. 在几何图形:等边三角形、正方形、正六边形和圆中,对称轴条数最多的是.8. 一个三角形的三边为2、5、x , 另一个三角形的三边为y、2、6,若这两个三角形全等,则x+y= .9. 如图,与关于直线对称,则的度数为 .
 10. 如图,已知△ABC≌△ADE,若AB=7,AC=4,则BE的值为 .
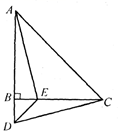
10. 如图,已知△ABC≌△ADE,若AB=7,AC=4,则BE的值为 . 11. 如图,在△ABC中,AB=AC,BD⊥AC,CE⊥AB,D、E为垂足,BD与CE交于点O,则图中全等三角形共有对.
11. 如图,在△ABC中,AB=AC,BD⊥AC,CE⊥AB,D、E为垂足,BD与CE交于点O,则图中全等三角形共有对. 12. 已知图中的两个三角形全等,则 .
12. 已知图中的两个三角形全等,则 . 13. 如图,在正方形网格中有两个小正方形被涂黑,再涂黑一个图中其余的小正方形,使得整个被涂黑的图案构成一个轴对称图形,那么涂法共有种.
13. 如图,在正方形网格中有两个小正方形被涂黑,再涂黑一个图中其余的小正方形,使得整个被涂黑的图案构成一个轴对称图形,那么涂法共有种. 14. 如图为6个边长相等的正方形的组合图形,则∠1+∠2+∠3=.
14. 如图为6个边长相等的正方形的组合图形,则∠1+∠2+∠3=. 15. 如图所示,AB=AC , AD=AE , ∠BAC=∠DAE , ∠1=25°,∠2=30°,则∠3= .
15. 如图所示,AB=AC , AD=AE , ∠BAC=∠DAE , ∠1=25°,∠2=30°,则∠3= .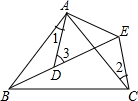 16. 如图,已知AB=12m,CA⊥AB于点A,DB⊥AB于点B,且AC=4m,点P从点B向点A运动,每分钟走1m,点Q从点B向点D运动,每分钟走2m.若P,Q两点同时出发,运动 分钟后,△CAP与△PQB全等.
16. 如图,已知AB=12m,CA⊥AB于点A,DB⊥AB于点B,且AC=4m,点P从点B向点A运动,每分钟走1m,点Q从点B向点D运动,每分钟走2m.若P,Q两点同时出发,运动 分钟后,△CAP与△PQB全等.
三、解答题
-
17. 计算(1)、(2)、18. 因式分解:(1)、(2)、19. 如图,在4×3正方形网格中,阴影部分是由5个小正方形组成的一个图形,请你用三种方法分别在下图方格内添涂2个小正方形,使这7个小正方形组成的图形是轴对称图形.
 20. 如图,在长度为1个单位长度的小正方形组成的正方形中,点A、B、C在小正方形的顶点上.
20. 如图,在长度为1个单位长度的小正方形组成的正方形中,点A、B、C在小正方形的顶点上.
⑴在图中画出与关于直线l成轴对称的;
⑵三角形ABC的面积为 ▲ ;
⑶以AC为边作与全等的三角形,则可作出 ▲ 个三角形与全等;
⑷在直线l上找一点P,使的长最短.
21. 已知:如图,点B,F,C,E在一条直线上,AB=DE,AC=DF,BF=EC.求证: ABC≌ DEF.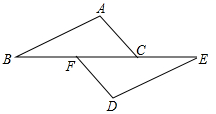 22. 如图,点E在CD上,BC与AE交于点F,AB=CB,BE=BD,∠1=∠2.
22. 如图,点E在CD上,BC与AE交于点F,AB=CB,BE=BD,∠1=∠2. (1)、求证: ;(2)、证明:∠1=∠3.23. 如图,AC是四边形ABCD的对角线,∠1=∠B,点E、F分别在AB、BC上,BE=CD,BF=CA,连接EF.
(1)、求证: ;(2)、证明:∠1=∠3.23. 如图,AC是四边形ABCD的对角线,∠1=∠B,点E、F分别在AB、BC上,BE=CD,BF=CA,连接EF. (1)、求证:∠D=∠2;(2)、若EF∥AC,∠D=78°,求∠BAC的度数.24. 已知:如图所示,A、B、C、D在同一直线上,AD=BC,AE=BF,CE=DF,试说明:
(1)、求证:∠D=∠2;(2)、若EF∥AC,∠D=78°,求∠BAC的度数.24. 已知:如图所示,A、B、C、D在同一直线上,AD=BC,AE=BF,CE=DF,试说明: (1)、DF∥CE;(2)、DE=CF.
(1)、DF∥CE;(2)、DE=CF.